Projective Geometry
The early years
Alexis Conrad
History of Mathematics
Rutgers, Spring 2000
The history of projective geometry is a very complex one. Most of the more formal developments on the subject were made in the 19th century as a result of the movement away from the geometry of Euclid. If one digs a little deeper, however, one can see th at the basic concepts upon which this branch of geometry is based can be traced back as far as the 4th century. These very early discoveries along with Euclid's Elements are the building blocks for the foundations that were laid down by the projective geometers of the 17th century. It is here that the history of the subject becomes most interesting. Great strides were made in the 17th century, but for some reason projective geometry did not become popular among mathematicians until the 19th century. Let us examine th e developments that were made in the 17th century, what things led up these discoveries, and the causes for the hundred-year lapse between these discoveries and their further development in the 19th century.
What exactly is projective geometry? On the surface, it is simply the study of the "properties of figures which remain unaltered (invariant) in projection." (Lanczos, 280) What is meant by projection? A very simple example is as follows. Look at a checke r board head on. All of the lines are parallel. Turn that same board at an angle keeping your perspective the same and what you see is quite different. The lines are no longer parallel. From a geometrical standpoint, what you are seeing is a projection of the lines of the checkerboard onto another plane. Projective geometry is the study of the properties of these lines after they have been projected. Early projective geometers found that while lengths, areas and angles were not maintained, there were prop erties of points and lines which were unaffected or invariant in projection. Using these discoveries they were able to construct new ways to solve old problems, and that is how this now highly regarded genre of geometry arose.
As defined above, projective geometry is the study of invariant properties. "The earliest projective invariant is a cross ratio of four collinear points." (Coolidge, 88) The cross ratio is a fundamental quantity in projective geometry, and is comparable to the notion of "distance" in traditional geometry. The distance between two points is a numerical value which describes a meaningful relationship between those points, because "distance" is invariant in metrical geometry. However, in the realm or projective geometry, this quantity does not remain invariant and is therefore useless. The cross ratio is an alternative which describes a relationship among four collinear points and also remains unchanged in projection. (Lanczos, 287)
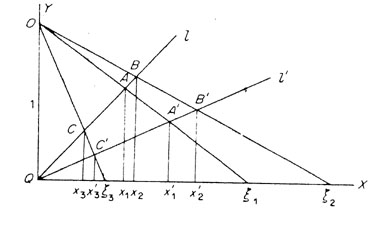
If four collinear points A, B, C, D are assigned the values (a),(b), (a + ub), (a + vb) respectively, then the cross ratio is defined as either v/u or u/v. (Coxeter, 177) The proof that this quantity is invariant is more complicated. The figure below shows the points A, B and C on the line l being projected onto the points A', B', and C' on the line l' from the perspective point O. We also see a series of points along the X axis labeled x, x' or x.

A summary of the proof that this figure illustrates is as follows.
The x's are expressed in terms of their corresponding
x
values. CA,
CB, C'A', and C'B'
are represented by (x3 - x1),
(x3 - x2),
(x'3 - x'1)
and (x'3 - x'2) respectively.
The ratio CA/CB simplifies to a
product in which the "position of the point C drops out"
(Lanczos, 288).
Then a similar result is produced by C'A'/C'B'.
This is important because then the ratio CA/CB : C'A'/C'B' is equal to a
function of x1 and
x2.
Because the position of the point C cancelled
out, we can then say that: CA/CB : C'A'/C'B'= DA/DB : D'A'/D'B'. This
can then be rewritten though properties of ratios as:
CA/CB : DA/DB = C'A'/C'B' : D'A'/D'B'.
Then we recognize that
CA/CB : DA/DB is in fact the cross ratio.
We can then rewrite this in
its more common notation; (AB, CD).
From this we have:
(AB, CD) = (A'B', C'D').
Therefore the cross ratio is invariant under
projection. It is uncertain who exactly is responsible for the
discovery of the invariance of the cross ratio, but it is known that
Pappus of Alexandria (290-350), who is considered by some to be the
discoverer of the "earliest truly projective theorems." (Coxeter, 3) ,
at least knew of its existence. Whether he in fact discovered it is
not certain. Pappus wrote a commentary on Euclid's lost book of
porisms and it is in that commentary that the earliest recording of
the cross ratio invariant is known. It is suspected h owever that
Euclid himself may have been aware of the invariant. (Coolidge, 89)
Let us now examine the Desargues Configuration:
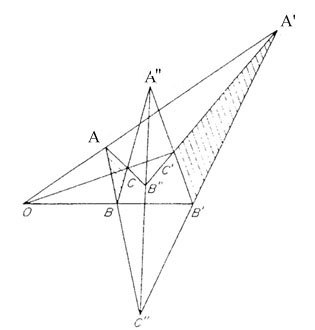
The Desargues Configuration is a simple yet intriguing example of the use of projection. What we see here is the projection of the triangle ABC onto a triangle A'B'C' in another pl ane. To understand this figure, it must be thought of it in three dimensions. The point O is the perspective point. An observer at the point O would not see both triangles. From that point, the triangle A'B'C' is exactly hidden behind ABC. Call the plane in which ABC lies P1, and the plane in which A'B'C' lies P2. The line AB lies in P1 while A'B' lies in P2 but we know they intersect because they both lie in the plane B'OA'. The point at which they intersect is called C''. This point C'' must lie on the line of intersection of the planes P1 and P2. By similar logic, the points B'' and A'' are marked as the intersections of lines AC with A'C' and of BC with B'C'. Just like C'', these points must lie on the line of intersection of the two planes. Thus all three lie on a single straight line, and they are collinear. What is even more fascinating about this configuration is that of the ten points in this figure, any one of them can be chosen as the point of perspective. With a few careful manipulations, this configuration can be reconstructed to work in the same way from the perspective of any one of the ten points. (Lanczos, 281)
This figure was named after the French mathematician Gérard Desargues (1591 - 1661) , who is considered by many to be the true founder of Projective Geometry. Desargues was an engineer and architect who became interested in the concept of projection. He was not however interested in projection on a strictly mathematical basis. Rather he expressed an interest in the education of artists and engineers (Kline, 288). He gave some lectures on the subject in Paris between the years 1626 and 1630. (Ball, 25 9) His most notable work, however was the Brouillon projet which was published in 1639. This essay dealt with conics. It was around Desargues' time that mathematicians were beginning to feel that Greek methods of proof were weak. These methods were not applicable in general, but rather were specific to each theorem. (Kline, 286) There was a desire to develop some uniformity in methods of proof. Desargues had studied the work of Apollonius and took an interest in simplifying his ideas of conics. He dev eloped new ways to prove many theorems on conics through the use of projection. Desargues published his ideas in his Brouillon projet of which he made only fifty copies, which he distributed among friends. Fermat, one of Desargues' contemporaries, was hi ghly impressed with the book and "regarded Desargues as the real founder of the theory of conic sections." (Kline, 289) Though Fermat's reaction was extremely positive, that appreciation was not shared in general among the mathematics community of the tim e. As a result of the lack of enthusiasm Desargues retired. It would not be for another hundred years that the brilliance of his work would be recognized.
Desargues was not the sole projective geometer of the 17th century. Two other mathematicians credited with work on the subject were Blaise Pascal and Philippe de La Hire. Pascal, influenced by Desargues, took a strong interest in projective geometry. He focused on simplifying the properties of conic sections. Pascal produced an essay that unfortunately was lost but was read by Leibniz who called it, "so brilliant that he could not believe it was written by so young a man." (Kline, 297) Pascal's is most n otable work in the field of projective geometry bears his name. Pascal's Theorem is as follows; "If a hexagon is inscribed in a conic, the three points of intersection of the pairs of opposite sides lie on one line." (Kline, 297) Though Pascal's exact proof of this theorem is not known (Kline, 297), the figure below illustrates one of many proofs which have since been proposed.
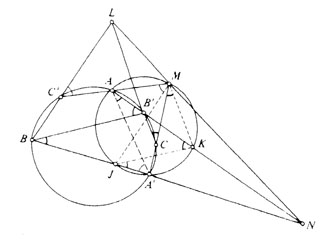
The specifics of this proof incorporate aspects of projective geometry which require more explanation than is convenient here. To summarize, the leftmost of the two circles is the "conic" in which the hexagon AB'CA'BC' is inscribed. L, M, and N are the three collinear points. Side BC' intersects with B'C at the point L, AC' with A'C at M, and AB' with A'B at N. The smaller circle to the ri ght is a projection of the conic. In this smaller circle, various projective properties are used to show all sides of the triangle JKM parallel to the corresponding sides of triangle BB'L. By a converse theorem, JB, KB', ML are parallel. "Parallel" has a very different meaning in projective geometry. Keep in mind that lines resulting from the projection of two parallel lines are not assumed to be parallel as well. In this figure, JB, KB' and ML intersect. Proving them "parallel" is simply one of several s teps in the projective reasoning which ultimately brings us to the conclusion that ML passes through the point at which JB intersects KB' which is the same point at which A'B intersects AB'. This point is also equal to N, which concludes the proof.
Philippe de la Hire was also heavily influenced by Desargues and strongly interested in projective geometry. He is most noted for his work, Sectiones Conicae ("Conic Sections"). This work dealt entirely with projective geometry. La Hire believed strongly that the methods of projection were stronger by far than Appollonios' methods. He thus attempted to prove all 364 of Appolonios' theorems. He came very close to this goal, proving 300 of them. (Kline, 298)
It is quite intriguing, when looking at the history of projective geometry, to see that following the many great advances of Desargues, Pascal, and La Hire, more than a hundred years pass during which the subject is virtually untouched. The work of Desargues was actually not appreciated at all outside the circle of his friends and colleagues at that time. (Kline, 289) What accounts for this lack of appreciation and why was it not until the early 19th century that this subject becomes popular? Essentially, it is said that Descartes' work on analytic geometry in the 18th century drew attention away from the "pure mathematics" of projection and towards more analytic genres. There are many theories as to why this occurred.
One thought is that Desargues' work lacked clarity. How can people appreciate something they cannot fully understand? Cynthia Cook stated in Western Mathematics Comes of Age that the ideas of Desargues were not popular among mathematicians of the time because while his definitions "helped to organize the rules of perspective for artists and craftsmen[,] ... their philosophical meaning was unclear." (Cook, 95) If his work appeared to some as simply a catalogue of the rules of perspective then that could be a legitimate explanation for the lack of enthusiasm in the mathematics community. In addition to this lack of apparent mathematical significance, Desargues also used some terminology that may have baffled his readers. For instance, he used the word "palm" to describe a straight line. Some of the words he used can also be found in earlier work of Alberti, but they were not in common use. It is the opinion of some that his choice of language made it difficult to understand the Brouillon Projet (Kline, 289). Could it be that Desargues' work, however brilliant, was so unclear as to delay the progress of projective geometry for a century? Let us explore other possible contributing factors.
It is also suggested that the interest of mathematicians of the 17th century involved discoveries which were applicable to science and technology and "[a]lgebraic methods of working with mathematical problems proved in general to be more effective . . ." w hile, ". . .[t]he qualitative results the projective geometers produced by their synthetic methods were not nearly so helpful." (Kline, 301) Analytic geometry was becoming increasingly more popular and historians believe that the reason for that is simply because it was more applicable to the needs of the time. There was an interest at this time in the use of mathematics to describe natural phenomena like motion, heat, and pressure. Analytic geometry allowed for the construction of curves to represent dat a which was much more conducive to creating "laws" of nature. "The interaction between the two modes of analysis (algebra and geometry) provided fresh insights into the nature of physical reality."(Cook, 97) Perhaps the clarity of Desargues' work was irre levant and it was inevitable that the birth of Analytic geometry would cast a temporary shadow on projective geometry.
Another thought is that perhaps projective geometry of the 17th and 19th centuries are more different than one would think and it is thus, not unusual for them to be separated by so many years. The difference is in the direction and intent of the geomete rs. As discussed earlier, the intention of Desargues and other projective geometers of his time was to better prove the methods of Euclid. They were "far from thinking in terms of new geometry." (Kline, 300) They were not thinking, as others of the time w ere, of advancement along the lines of "new geometry," but rather in terms of improving upon what already existed. However, Rouse Ball in his work, A Short Account of the History of Mathematics, states that in the 17th century, "Greek mathematics was not capable of much further extension, mathematicians were beginning to seek new methods of geometry." (Ball, 258) In the 19th century, projective geometry is reborn as a result of the development of several new non-Euclidean branches of geometry. Perhaps it was necessary to view projection as "new" in order to make advancements.
We have explored several possible causes for the initial neglect of projective methods in the 17th century, as contrasted with its rebirth in the 19th century, and while these potential causes differ considerably, one can detect a common theme. Mathematics was simply not ready for projective geometry in the 17th century. Analytic geometry had to come first. Perhaps Desargues was before his time, or perhaps he didn't even see projective geometry the way it would eventually come to be seen in the 19th centur y; as an independent branch. Regardless, the subject was eventually reborn and historians now refer to the ideas of Desargues as "fundamental to our understanding of space and time." (Cook, 95)