The development of mathematics over the course of the last four millenia shows a steady though sometimes slow advance, with one mathematician's ideas greatly stimulating those of his successors. A classical example of this tendency was the crescendo towards the development of the differential and integral calculus, crowned by the work of Newton and Leibniz in the seventeenth century. By no means did these two individuals formulate completely original concepts, but rather connected all the miniature steps achieved by previous mathematicians into a coherent, usable form that all the mathematical world could use regardless of their level of expertise. While Newton and Leibniz made the same connections and discoveries, the latter's methods are more generally adopted in our textbooks today, as Leibniz succeeded in bringing a complex topic to a level of generality easily understood and accessible for various mathematical purposes, strengthening the theory of integration, and making it into one of the most essential of all mathematical techniques.
Although he did not begin his academic career in mathematics, the intellectual giant Gottfried Wilhelm Leibniz (1646-1716), a genius in every sense of the word, became fascinated in the subject matter when he came to France in the 1670s (Edwards 231). As he read through the material, he often commented on the methods and techniques employed, noting how he would interpret these results and their significance to the mathematical community. He tried to present a problem in the manner easiest for himself to grasp, and this prompted his interest in the possibility of creating a formal language that all educated individuals would be able to comprehend and use. His ultimate goal was to create a system of notation and terminology that would codify and simplify the essential elements of all logical reasoning, to provide all educated people with the powers of clear and correct reasoning (Edwards 232). This goal he achieved in the limited context of the calculus. In addition to its simplicity, his system provided a method for investigating continuity in all its manifestations, a principle long explored and never previously mastered (Bell 363) 1. Now both mathematicians and scientists possessed the ability to deal with what had previously been the most difficult issues within a system that was easily understood and well defined. Long had integration been explored, but now it had finally matured through the brilliant, sometimes misunderstood, workings of Leibniz's mind. Perhaps his influence was best understood when L'Hopital stated , "His Calculus has carried him into Countries hitherto unknown; and he has made Discoveries by it, astonishing to the greatest Mathematicians of Europe." (Harman 385) Perhaps for the purpose of displaying his discoveries, or possibly for the extended circulation of mathematical ideas in general, Leibniz was influential in the formation of a major scientific journal named the Acta Eruditorum of Leipzig in 1682 (Weil 162).
One often asked question addresses the validity of Leibniz's claim to have made original discoveries, dated between 1672 and 1676, as opposed to simply the reworking of Newtonian ideas, conceived a decade earlier (ostensibly in 1665) but remaining unpublished for twenty years, into a more manageable formulation (Eves 332-333). With extensive research and thorough analysis, historians have concluded that it is feasible that Leibniz arrived at his conclusions independently, and that rather than Newton, Barrow and Pascal appear to have been more influential upon his studies (Smith 619). One piece of evidence supporting this assertion is that Leibniz led a rather secluded existence when he was engaged in his mathematical period. Very often, this seclusion caused him to develop mathematical concepts previously conquered, reinforcing the possibility that the calculus was an example of one such. Other mathematicians claim that it is "immaterial" whether Leibniz's fundamental ideas came from Newton (Ball 353), as the importance of his work lies in its being another way of solving an identical problem, which is not affected by priority. Even if knowledge of Newton's methods had somehow fallen upon Leibniz, as a tool, the latter's methods would be employed as they are today, due to his implementation of a convenient symbolism and an insistence upon following rigid algorithms. Despite all the greatness of Leibnizian methods as seen in modern eyes, Newton's method was preferred until the mid-19th Century, when Riemann amended the calculus with ideas better suited to Leibnizian methods and his idea of integration as a limiting summation (Development 481).
Like all other aspects of Leibniz's studies, the notation he
implemented in his commentaries and, later, in his original work often
metamorphisized, depending on his interpretation of the material he
was studying and his belief of the most efficient symbo lism possible.
With no style or structure to aid in a historian's complete grasp of
his exact thoughts at any given time, it was not uncommon to see a
shift from one representation to another as he strove for a symbolism
that would allow those who were n ot brilliant mathematicians to
understand his work. For example, the sign for equality, which is
= in present day form, varied in his work from a form of
= in 1666, to ![]() in
1675, to either aequ. or aeq. in 1679, and back to = in 1684
(Cajori 187). Another oddity in his work involved his diagrams, as
influenced by the work of Fabri, Leibniz commonly depicted the x-axis
as a vertical line rather than in the now customary horizontal fashion
(Hofmann 50). In addition, he generally did not make use of a y-axis,
stating that it was unnecessary and tended to restrain the conditions
and generality of a function 2.
in
1675, to either aequ. or aeq. in 1679, and back to = in 1684
(Cajori 187). Another oddity in his work involved his diagrams, as
influenced by the work of Fabri, Leibniz commonly depicted the x-axis
as a vertical line rather than in the now customary horizontal fashion
(Hofmann 50). In addition, he generally did not make use of a y-axis,
stating that it was unnecessary and tended to restrain the conditions
and generality of a function 2.
His symbolism for integration experiences the same sort of
transformation, making it hard at times to follow Leibnizian ideas in
anachronistic interpretations. When first introduced in 1675,
integration is referred to using the phrase "omn. ![]() " or "omnes
" or "omnes ![]() ", meaning all the
", meaning all the ![]() summed together, and he indicates double
integration by
summed together, and he indicates double
integration by ![]() ; the line
above, called a vinculum, shows that one is taking the sum of
the sums of all the
; the line
above, called a vinculum, shows that one is taking the sum of
the sums of all the ![]() 's
(Cajori 187). Later that year, Leibniz switched to the present-day
integration sign
's
(Cajori 187). Later that year, Leibniz switched to the present-day
integration sign ![]() , favored
the symbol
, favored
the symbol ![]() in 1686 in Acta
eruditorum, and returned to
in 1686 in Acta
eruditorum, and returned to ![]() in 1691 (187). When he stated the fundamental theorem
of calculus, he used the notation
d
in 1691 (187). When he stated the fundamental theorem
of calculus, he used the notation
d![]() x aequ. x (187).
Part of the reason for the inconsistencies in Leibniz' notation lies
in his willingness to adopt modifications in response
to his correspondents' opinions.
x aequ. x (187).
Part of the reason for the inconsistencies in Leibniz' notation lies
in his willingness to adopt modifications in response
to his correspondents' opinions.
As previously stated, Leibniz was greatly concerned with clarity
and desired input on whether he had made a rational and easily
understood choice. Leibniz settled on the conventional symbol for
integration after conferring with his esteemed colleague Johann
Bernoulli, who preferred the symbol I and the name calculus
integralis. "As regards signs, I see it clearly that it is to the
interest of the Republic of Letters and especially of students, that
learned men should reach agreement on signs. Accordingly I wish to
get your opinion, whether you approve of marking by the sign ![]() the sum, just as the sign
d is displayed for differences; ... Perhaps it will be well to
examine other symbols, concerning which more on another occasion."
(Leibniz in Cajori 182) As seen, Leibniz favored the
the sum, just as the sign
d is displayed for differences; ... Perhaps it will be well to
examine other symbols, concerning which more on another occasion."
(Leibniz in Cajori 182) As seen, Leibniz favored the ![]() , an elongated s, and was partial
towards the name of calculus summatorius. He realized,
however, that his personal preferences were not necessarily the best
notations, just as many of the notations used by mathematicians he had
researched were mystical in their meaning and origin. It is obvious
that Leibniz thought of integration as a form of summation, choosing a
symbol similar to the letter s to show this relationship. In
the end, he and Bernoulli compromised, settling on Leibnizian
symbolism, with the name suggested by Bernoulli (181).
, an elongated s, and was partial
towards the name of calculus summatorius. He realized,
however, that his personal preferences were not necessarily the best
notations, just as many of the notations used by mathematicians he had
researched were mystical in their meaning and origin. It is obvious
that Leibniz thought of integration as a form of summation, choosing a
symbol similar to the letter s to show this relationship. In
the end, he and Bernoulli compromised, settling on Leibnizian
symbolism, with the name suggested by Bernoulli (181).
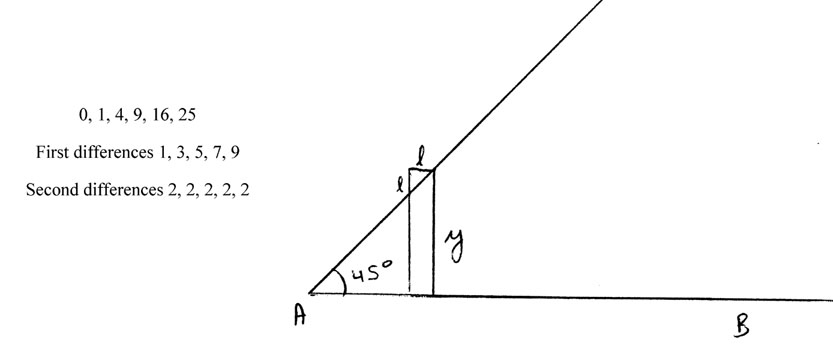
For a basic understanding of the integral, Leibniz examined the
sequence of the squares, their first differences, and their second
differences, noting that if one starts from 0, the summation of the
differences up to a point yields the square value at tha t given
point. In this case the change in x, given in his notation with a, is
1 as we count up the natural numbers, squaring each one while
the change in y is denoted with l. As a result Leibniz
stated that omn. l = y. Now he examines the following
triangle and sees that the area beneath would be x2.
If he broke this down into rectangles, he could determine the area of
the triangle by finding omn. yl. He knew that, since y =
omn. l, this was equal to omn. omn. l l/a , where the
a seems to be his differential. Since he knew that omn. yl
= y2/2, therefore y2/2 = omn. omn. l
l/a or, in our terms, equal to ![]() {
{![]() dy} dy/dx
=
dy} dy/dx
= ![]() y dy/dx (Kline
372-3, from Leibniz' manuscripts). So Leibniz gives here an
elementary example in conformity with his goal of universal
understanding. Modern mathematicians would argue that he has
forgotten a constant after the integration, but, as in all examples he
uses, the equation passes through the origin, meaning we have an
initial value of zero for our function.
y dy/dx (Kline
372-3, from Leibniz' manuscripts). So Leibniz gives here an
elementary example in conformity with his goal of universal
understanding. Modern mathematicians would argue that he has
forgotten a constant after the integration, but, as in all examples he
uses, the equation passes through the origin, meaning we have an
initial value of zero for our function.
Leibniz went on to derive the equivalent of integration by parts from a similar geometric argument, which yielded in his manuscript omn. xl = x omn. l - omn. omn. l. He set l = x and the relation became omn. x2 = x omn. x - omn. omn. x. Since he has shown that omn. x = x2/2, the problem becomes omn. x2 = x x2/2 - omn. x2/2. He added omn. x2/2 to both sides and divided by 3/2, yielding a final answer of omn. x2 = x3/3. So Leibniz demonstrated how integration by parts worked by first examining it geometrically, then solving an example algebraically. It is highly probable that this geometrical solution, or at least the basis for it, was obtained from his studies of predecessors' notes as the concept had been around for years, but with no proper presentation.
Leibniz' review of earlier work included an examination of Pascal's method for finding the moment of a quadrant of a circle about the x-axis, a concept based on Archimedes' determination of the surface of a sphere 3.
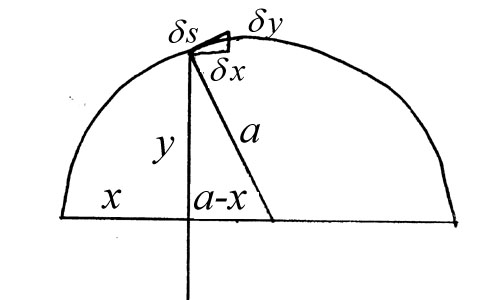
For the given arc, the center was found and a horizontal line was
constructed as the x-axis such that it passes through this point. A
perpendicular to the x-axis was then drawn given that it passed
through a given point on the arc, forming
a the larger triangle shown with sides y, a, and a-x. Now a triangle
was constructed from the tangent to the point as the hypotenuse, one
side being a line parallel to the x-axis and the other being parallel
to the side y in the previous triangle. Through Euclidean
geometry, it is possible to prove similarity of the triangles,
implying the equation 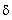 s : a
=
s : a
= 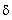 x : y 4, which can be transformed into the
equation y
x : y 4, which can be transformed into the
equation y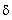 s = a
s = a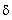 x. Since Pascal was looking at
one quadrant, he was looking for the area under the curve from 0 to
one fourth of the circumference of the circle on which the arc lies.
Looking at this area in terms of our x-axis, the x
varies from 0 to a, meaning that
x. Since Pascal was looking at
one quadrant, he was looking for the area under the curve from 0 to
one fourth of the circumference of the circle on which the arc lies.
Looking at this area in terms of our x-axis, the x
varies from 0 to a, meaning that ![]() y
y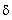 s =
s = ![]() a
a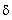 x = a2 5.
x = a2 5.
Leibniz realized that this process could be generalized to include a more extensive collection of curves as the process can be duplicated if a represented the normal to the curve. A discovery made by the spring of 1673, this represented his understanding of geometry while also showing his ability to take an analysis of a specific cas e and extend it to represent all such examples (Hofmann 49). Leibniz's realization that this example had more relevance than to the specific case in which Pascal had analyzed showed his desire to generalize an arc, unlike Pascal's methods, providing the fire for his general theories and equations of integration.
Another example of previously discovered material helping Leibniz
to formulate his version of the calculus was Cavalieri's method of
indivisibles, which focused on dividing the area under a curve
up into an extremely large number of small rectangles. Up on further
examination, Leibniz realized that this method could be duplicated
using triangles sharing a common point as a vertex. Given the
diagram6, below,
where the arc AB must be smooth and convex, 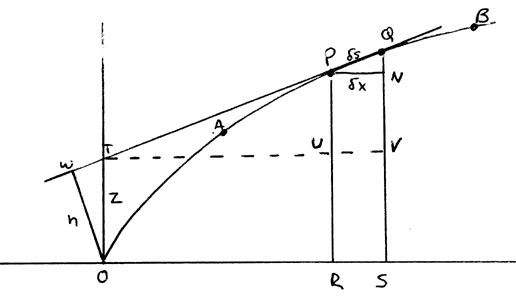
the actions are similar to Cavalieri's as
Leibniz sums areas of the divisions, carefully subtracting any excess
area that might arise. If AB is extended such that it intersects the
x-axis at point O, three vertical lines can be constructed, one
passing through this intersection, another through A, and the third
through B . If two neighboring points, P and Q, on AB are chosen, a
line can be drawn connecting them while intersecting at T the vertical
line passing through O. Drop vertical lines from P and Q in a similar
fashion to the methods used for A and B, with them int ersecting the
x-axis at R and S, respectively. Using the line segment PQ as the
hypotenuse, one side a line parallel to the x-axis passing through P
and intersecting QS at N, and the second side as QN, construct a
triangle PQN.
Leibniz noticed that since P and Q are chosen such that they are
very close on AB, then the triangle can be labeled using methods
similar to the slope for a line with PN equivalent to dx, or the
change in x, and PQ by ds, or the change in the line segment .
Leibniz now constructed OW, labeled as h and passing through QT at W
given that 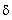 x : h =
x : h = 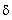 s : z, with z representing the
segment OT. It followed that z
s : z, with z representing the
segment OT. It followed that z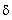 x = h
x = h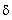 s and that the area of OPQ was equivalent to 1/2
the area of RSVU, showing the mathematical community it was
possible to transform a problem of concurrent slices into the
quadrature problem long dealt with by previous mathematicians.
s and that the area of OPQ was equivalent to 1/2
the area of RSVU, showing the mathematical community it was
possible to transform a problem of concurrent slices into the
quadrature problem long dealt with by previous mathematicians.
Leibniz continued on, using the theory of tangents, to say that
z = y - x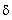 y /
y / 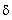 x 7. Using the fact
that arbitrary changes in the representation of variables of an
integratable function in differential form does not change the value
for the function when integr ated, a concept which supplied the
knowledge necessary for present-day integration by substitution,
Leibniz substituted to facilitate the integration (Edwards 234). So
now 1/2
x 7. Using the fact
that arbitrary changes in the representation of variables of an
integratable function in differential form does not change the value
for the function when integr ated, a concept which supplied the
knowledge necessary for present-day integration by substitution,
Leibniz substituted to facilitate the integration (Edwards 234). So
now 1/2![]() zdx = 1/2 xz -
1/2
zdx = 1/2 xz -
1/2![]() xdz.
xdz.
Now, in an attempt to find the special case for a quadrant of a
circle with a radius equal to one, Leibniz applied the rule of
tangents to yield x = z2/(1+z2)8. He then used the
binomial expansion, integrated and evaluated each term separately,
added the unaccounted triangular area unaccounted for, and the result
was a value of 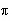 /4.
/4.
This case was significant as it showed how one could make a substitute leading to an integrable function (that is, one whose antiderivative was explicitly known). Other than Newton, this idea was original, but Pascal and others had considered the underlying premise on which it was built. Much of the analysis depended on geometry that was included in the Euclidean Elements and had been known to mathematicians for about 2000 years. In this case, Leibniz was able to generalize the case and show how his method would yield a verifiable answer. This problem appears to be the foundation for Leibnizian integration as it combines the principles of area from geometry with the new method consistently. Furthermore, this example shows how the previous examples given by mathematicians were not specific enough to allow answers to be found. In this sense, Leibniz had found a case where others had shown Leibniz the path he must follow and he took the initiative to formulate a method.
After Leibniz's form of integration had been presented, speculation arose, especially in response to infinitesimal measurement he implemented. In response to this speculation, he stated "... to avoid these subtle matters of dispute and because I wanted my ideas to be generally understood, I contented myself with explaining the infinite as the incomparable. In other words, I assumed there were quantities which were incomparably larger or smaller than ours." (Leibniz from Meschkowski 58) He went on to say that there are different degrees of infinitesimal units, but each one has a value which can vary so that it is possible to choose a value lower than the one chosen. He understood that the infinite sum of units with a thickness infinitely small is a modi fied form of the summation problem commonly dealt with by his predecessors. Further discussion on Leibniz's behalf went as follows: "For if an antagonist denies the correctness of our theorems, our calculations show that the error is smaller than any giv en quantity, since it is in our power to decrease the incomparably small." (58) This explanation does appear problematic though as he is stating the summation of the error cannot be significant since the "incomparably small" units are not significant enough to have too much error. By this argument there would be no measure when one took the integral since the units are too small to be accounted for. This argument shows that Leibniz had particularly amazing and revolutionary methods for solving these pr oblems, but the rationale he based this on was not rock solid since he was not a stickler for details of a proof.
One cannot address Leibniz and integration without regarding the controversy that arose between himself and Sir Isaac Newton over the priority of their methods. As previously stated, Newton's methods were formulated in 1665 while Leibniz did not invent h is method until about eleven years later. The debate took the form of challenge problems and slander, causing educated men to act like school children, but like everything else Leibniz encountered in his mathematical career, there was a positive outcome.
Previously the mathematical world had been fairly disorganized, and communication of ideas was severely inadequate. With the controversy festering, communication among mathematicians began to become more efficient as they now felt more urgency to interact with their peers. With this a community was formed that stayed adrift with all the significant news in the world of mathematics as a trend of establishing journals, scientific societies with recording secretaries, and full-fledged book trades began (Harman 385). Even after the controversy had passed, the community remained, ensuring efficiency in the sharing of cutting-edge formulations.
Much of Leibniz's efforts can be compared to the efforts of present-day historians to examine his mathematical career. In both cases, it is necessary to acquire as much information possible in order to formulate one's own opinion on a prospective outcome. By no means did Leibniz accomplish as much as some other mathematicians, but Leibniz knew how to analyze the information he accessed. After taking the necessary steps in integration of compounding ideas of many predecessors, he showed his true worth by c ontinuing his studies and following a passion that may not be adhered to as much as should be. It appeared that he cared more for a general understanding for the entire mathematical world than impressing a certain few peers with amazing mathematical abil ity. As a testament to how successful he was in this quest, students who have no desire in learning math can understand the concepts, an act Leibniz's predecessors would surely have failed miserably. The amazing influence of Leibniz even extends to assisting, partially directly and somewhat indirectly, in improving the communication between scholars, showing the importance of documenting all information and providing it to a large audience. Justice was served as a man whose success arose from his concern with maintaining excellent communications with his peers created a situation in which all mathematicians could remain informed of each others' research activity, and have access to all essential information.
Notes
1. Newton's version of the calculus also tackled this issue.
2. In many accounts of Leibniz's work, diagrams tend to include the y-axis, as in Edwards 246, but this is the result of historians including modern formulations in problems that pre-dated the techniques. In general, it seems that confusion exists because commentators attempt to plot all graphs so that modern mathematicians recognize the notation and do not have to interpret an older system. This most certainly develops from many books similar to Edwards being written as a math text instead of a historic al text.
3 As detailed in Leibniz in Paris; 1672-1673 by J.E. Hofmann. He does appear to show some modernization of the methods and, for that reason, I have attempted to describe the problem in a mindset more similar to Leibniz's time.
4 This symbolism is in a proper style for Leibniz, as shown in Cajori 189, as he adopted this notation in 1676. It is not known however if this was the notation used by Pascal also, but Leibniz's adoption of this problem would suggest that he enjoyed Pas cal's style and would be more likely to adopt the notation, or one very similar in style.
5 Pascal did not use the symbol commonly used for integration today because it had not been introduced yet. One can use it, though, as a representation of Pascal's chosen process for integration.
6 As given in Leibniz in Paris: 1672-1676, by J.E. Hofmann on p. 55. It may be interesting to note that this example was muddled by C.H. Edwards, Jr. in The Historical Development of the Calculus on p.246 as he failed to clearly identify the diagram and incorrectly assumed that Leibniz was working with both an x and y-axis.
7 Due to similar triangles PQN and TQV, dy : y-z = dx : x. So then xdy = (y-z)dx, xdy/dx = y-z, and z = y - xdy/dx.
8 In this case, the common vertex is at the center of the arc and F = the angle measure between the x-axis and the radius connected to the lower value on the arc P. So then x = 1 - cos F = 2sin2(F/2). Similarly, it can be found that z = tan (F/2). Sinc e it is known that sin2a = tan2a/(1+tan2a), then x = z2/(1+z2).