Fibonacci
Christopher O'Neill
History of Mathematics Term Paper, Rutgers, Spring 1999


Leonardo Pisano Fibonacci was born in 1170 in Pisa [1, p. 604]. His name at birth was simply Leonardo, but in popular works today he is most commonly referred to as Fibonacci (from filio Bonacij, literally meaning son of Bonacci, but here taken as of the family Bonacci, since his father's name was not Bonacci, according to [1, p. 604]). Interestingly enough there is no proof that Fibonacci was known as such in his own time, and it has been suggested that the name Fibonacci originated with Guillame Libri [3, xv]. Fibonacci was also known by the nickname "Bigollo", which may be taken to mean loafer, and may have expressed the general lack of interest in the purely theoretical mathematics Fibonacci showed interest in. However Bigollo may also be interpreted as "well traveled", which adequately describes Fibonacci [2]. However these explanations of the nickname Bigollo have also been termed "fanciful", and having "no merit" [3, xv]. Fibonacci used the name Leonardo Pisano, which simply made reference to his origin in the city of Pisa. Now that the many names of Leonardo Pisano Bigollo Fibonacci have been set forth, from this point on I will simply refer to him as Fibonacci.
Fibonacci was born in 1170 to Guilielmo, a member of the Bonacci family. Guilielmo held a position as a secretary of the Republic of Pisa , in the Province of Tuscany, which at the time was part of the Holy Roman Empire, and today is in northern Italy [1, xv]. In approximately 1192 Guilielmo was posted to a trading center in the city of Bugia (now known as Bougie [1, p. 604] or as Bijaya by the Arabs [4]), which is in northeastern Algeria, and lies fairly close to Italy, across the Mediterranean Sea. Guilielmo brought Fibonacci to Bugia when he accepted this position. In Bugia Fibonacci learned a great many things - notably, from the point of view of the history of mathematics, the Indian numerals. Fibonacci wrote of his stay in Bugia in the Liber abbaci [2] as follows:
When my father, who had been appointed by his country as public notary in the customs at Bugia acting for the Pisan merchants going there, was in charge, he summoned me to him while I was still a child, and having an eye to usefulness and future convenience, desired me to stay there and receive instruction in the school of accounting. There, when I had been introduced to the art of the Indians' nine symbols through remarkable teaching, knowledge of the art very soon pleased me above all else and I came to understand it, for whatever was studied by the art in Egypt, Syria, Greece, Sicily and Provence, in all its various forms.
In his travels Fibonacci learned a great deal of mathematics, including the Indian numerals, and also a great many of the Greek classics which had been lost to the west, but whose Latin translations had been preserved in the east through the long endurance of the Roman empire in Constantinople [1, p607]. Fibonacci ended his travels in approximately 1200 and settled down in Pisa, where for the next twenty five years he composed a number of texts in which he did important work in number theory and the solution of algebraic equations among other important things. He also came upon the series of numbers known today as the Fibonacci numbers. Fibonacci gained recognition in the court of Emperor Frederick II. Fibonacci is believed to have died around 1250, but in any case some time after 1240; there are no records of him after this date [3].
Fibonacci's first major work was the Liber abbaci ("The Book of Calculations" [5]) written in 1202. The Liber abbaci was subsequently re-edited by Fibonacci himself in 1228. In the Liber abbaci Fibonacci presents an overview of basic arithmetic and algebra. First he discusses common finger computations and the use of Roman numerals, which were common computational methods in Europe at that time [1, p. 608]. Next he introduces the Indian numerals. The Liber abbaci begins"These are the nine figures of the Indians: 9 8 7 6 5 4 3 2 1. With these nine figures, and with the sign 0 which in Arabic is called zephirum, any number can be written as will be demonstrated [5]." Next he explains the Arabic rules for working with the Indian Numerals [1, p. 606]. Fractions are placed to the left of integers, and the fraction bar is used. The basic rules for these are outlined below (the examples are based on examples in the Dictionary of Scientific Biography, p. 607 and Lüneburg, pp. 68-81.)

The Liber abbaci also examines root extraction, and a variety of
word problems, which include many classical problems similar to those
in ancient Egyptian sources [1, p. 606]. Many of these word problems
lead to problems in indeterminate analysis, such as this example [1,
p. 606]:
The name indeterminate analysis refers to the fact that the set of equations is underdetermined: there are four unknowns `b,x,y,z' and only three equations, so that a unique answer is not possible, but only a relation between values of the variables.
The Liber abbaci also contains many practical problems of value to merchants of the time, ranging from the calculation of interest to problems concerning currency exchange rates and profit margins. Also contained in the Liber abbaci are a variety of problems and puzzles including a famous problem on the reproduction of rabbits, which will be examined below.
Fibonacci's second work is entitled the Practica geometriae, and was composed ca. 1220-1221. The Practica geometriae draws heavily on the works of the ancient Greek masters, including Euclid and Archimedes. Fibonacci also draws on the works of Plato of Tivloli (1145) [1, p. 609]. Fibonacci's discussion leads often to quadratic equations, in whose solution he shows adept skill, even taking notice of their multiple solutions. Included in the Practica geometriae are many instructions given for the practical surveyor. Simplified instructions are given for measurement, and easily read tables are given where complex computation would have been necessary to obtain the solution. Archimedes' method of determination of ? from inscribed and circumscribed polygons is discussed. Indeterminate problems that follow from these lines of thought are also treated.
The work Flos, composed in 1225, was sent to Emperor Frederick II as a response to questions set forth by Johannes of Palermo (a member of Emperor Frederick's court and a friend of Fibonacci's [3]). The first problem was the solution of the equations x2+5=y2 and x2-5=z2. The next problem is the solution of the third order equation x3+2x2+10x=20. Fibonacci showed that the solution of the equation was not a whole number, a fraction or any of the Euclidean irrational magnitudes. He does however go on to provide a rational approximation of the solution. The third and final problem is the solution of a series of indeterminate equations.
In the Liber quadatorum composed in 1225 Fibonacci obtains many notable achievements in number theory. He gives a variety of methods for finding Pythagorean triples. He next goes through a definition for a special class of numbers he calls a congruum, and then through a brilliant proof obtains the full solution of the set of indeterminate equations set forth by Johannes of Palermo.
Fibonacci did not express his mathematics in the form of equations as is done today, but he did however word them in such a way as to be directly translatable into modern equations: an example from the Liber quadatorum [3, p. 4] runs:
These four works and a letter to Theodorus (Epistola ad Magistrum Theodorum [3, xix]) comprise the surviving works of Fibonacci. These however are not the only works composed by Fibonacci. Other works known to have existed include the Di minor guisa , a book for commercial arithmetic. A discussion of Book X of Euclid's Elements is also known to have existed, in which Fibonacci provided a numerical discussion of irrational numbers.
A brief discussion of a few of the mathematical achievements of Leonardo Fibonacci will now be undertaken.
The discussion of the Fibonacci numbers, while of only minor importance to the works of Fibonacci, has such great notoriety that it would be negligent to ignore it, so a discussion of the Fibonacci numbers and a few interesting applications of the Fibonacci numbers is given in Appendix A.
The most well known of Fibonacci's achievements is definitely the Fibonacci sequence. The Fibonacci sequence was the first recurrence series, other such series as the Lucas series are modelled on it. Fibonacci numbers have applications in modern mathematics. They are often used in modern computer science, as a part of number theory, and in the counting of mathematical objects.
What some consider his most important accomplishment to be the introduction of Hindu-Arabic mathematics into western culture, this is not considered by some to be a great mathematical feat, but rather a compilation of known techniques for a new audience (somewhat equivalent to the statement that Euclid was not so much a mathematician as the author of a successful textbook)
In his work, Fibonacci put forth not so much an original exposition (although he showed a certain amount of innovation in some of his solutions) as a compilation of the techniques of Arabic arithmetic and algebra.
Interestingly enough Fibonacci was also responsible for the introduction of Arab mathematics to the Arabs as well. Arabic mathematics were originally in use only by scientists and mateticians but not by the Arab businessman [3, xviii].
"[Fibonacci] can rather be credited with the introduction of scientific calculating techniques into general business practice [3, xviii]."
These are really only a few of Fibonacci's many achievements, A student both of the algebraic heritage of the east and a scholar of the ancient Greeks, "He joined the theoretical traditions of the Hellenes and the algebraic traditions of the Arabs and established them in Europe. [3,xx]." Fibonacci has been called "the first great mathematician of the Christian West" [1, p611]. It seems an accurate title for the man who had a major part in recognizing the usefulness of and introducing the system the system of numbers we use still today, for the man who has provided a foundation for modern number theory, and many other useful parts of mathematics.
The best known work of Fibonacci concerns the Fibonacci numbers, first examined in the Liber abbaci through the rabbit problem.
A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive.
From this statement the famous Fibonacci numbers can be derived.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...
where the first two numbers of the series are 1 and 1 and each numbers afterwards is defined as the sum of the two previous terms, Fn=Fn-2+Fn-1. (Though in Fibonacci's sequence the first number was 1 and the second number was two, the first one was assumed)
The genealogical tree is shown below:
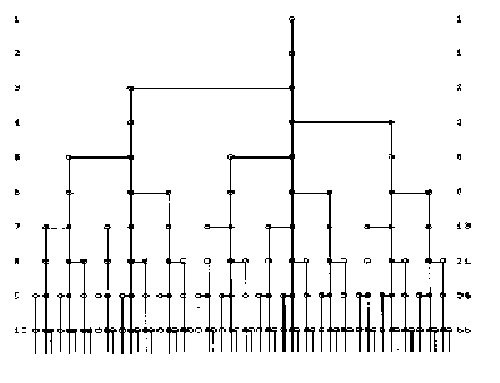
The definition of the Fibonacci numbers is an example of what we refer to today as a recurrence relation. The Fibonacci numbers involve the golden ratio (the solution to the equation x²-x-1=0), which was known already to the ancient Greeks. The ratio of successive Fibonacci numbers appears, on inspection, to converge to a number around 1.618. If we assume that these ratios do converge to a limit, then for large indices we have
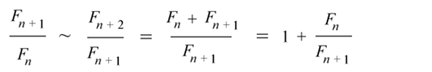
Accordingly the limit (assuming it exists) of these ratios, which we will refer to as phi, satisfies the equation phi=1/phi+1, and so phi²-phi-1=0, whose positive solution is the golden ratio.
Using this quantity phi, the Fibonacci numbers can be defined explicitly by a formula which is known as Binet's equation:
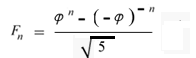
 ...
...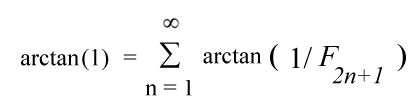 .
.
The Fibonacci numbers can be seen in a wide variety of places in mathematics including certain diagonal sums in Pascal's Triangle:
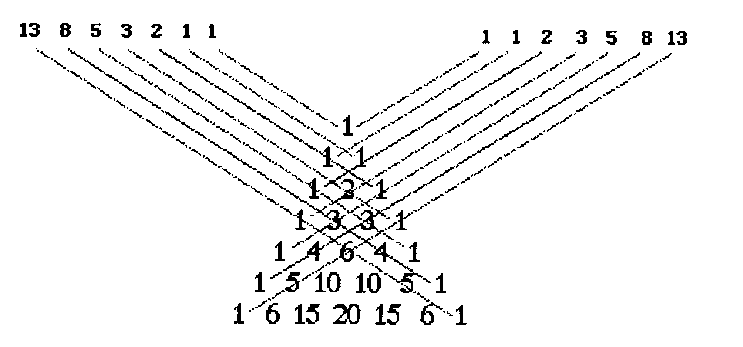
There even exists today a journal entitled the Fibonacci Quarterly devoted entirely to the study of the Fibonacci numbers.
The following additional references, though not directly cited, were used to add to my general understanding of the topic, and to clarify some poorly explained points in the cited references.