![]()
We consider two applications of the method of using eigenvalues and eigenvectors.
Markov Chains
We have already considered matrices that describe changes from one numerical configuration to another. Such changes can correspond to probabilistic ones - each state in a configuration changes to another state in the configuration, or does not change, with a certain probability between 0 and 1, and the total probability of all possible outcomes for each input state is 1.
Def. A Markov chain is a process that consists of a n states and known probabilities pij, with each pij representing the probability of moving from state j to state i. Here 0 < pij <1, and p1j + · · · + pnj= 1, for each j. The transition matrix of the Markov chain is the matrix A = [pij].
Notice that each of the columns of
the transition matrix
has nonnegative entries that sum to one.
Such a matrix is called stochastic.
The transition matrix describes the change from one configuration x (or collection of states) to another Ax under the given probabilities. If x itself is a probability vector (that is, a vector with nonnegative entries that sum to one) representing the probabilites of the various states initially, then the entries of Ax represent the probabilities of the various states after one transition. Clearly Akx describes the probabilities of the various states after k transitions. If it is possible (meaning with nonzero probability) to move from anystate to any other state after finitely many steps, then for any given position in the n x n array, Ak has a nonzero entry in that position for some k. The Markov chain is called regular in this case, and it can be shown (but we will not show it) that for the transition matrix of a regular Markov chain, there is a k such that Ak has all entries nonzero, and that the following result holds.
Theorem
Let A be a regular
n x n transition matrix. Then
(a) 1 is an eigenvalue of A;
(b) there is a unique probability vector
vwhich is an eigenvector of A corresponding to
the eigenvalue 1;
(c) for any probability vector p,
the vectors
Akp
approach v as
k goes to infinity.
Example
An important example in one variable calculus of a differentialequation with many physical applications is the equation dy/dt= ky, for some constant y. We know that solutions are of the form y = Cekt, for a choice of C determined by a side condition.
Now, if we have several quantities y1, . . ., yn, which independently satisfy differential equations of this same type, of the form dyj /dt= kjy, then the solutions are similarly described. Moreover, if we consider the vector y (depending on the variable t) whose coordinates are the yj, and let D be the diagonal matrix with diagonal entries k1, . . . , kn, then the whole system of differential equations can be written as dy/dt= Dy. Any such diagonal system is just a set of independent differential equations, and is no harder to solve than in the case of a single equation.
However, more complicated systems allow for rates of change dyj/dt which are determined (linearly) not only by the function yj, but by the other functions yi as well. A linear system of this form can be written dy/dt = Ay, for some n x n coefficient matrix A. If A is diagonalizable, we will be able to solve this system by reducing it to the easy diagonal case.
If A is diagonalizable, we have A = PDP-1 for P invertible and D diagonal. Therefore, we can write P-1A = DP-1. Now set z = P-1y (i.e., y = Pz). Then (using the usual facts about derivatives of sums and scalar multiples) we have
dz/dt =
P-1
dy/dt= P
-1
Ay=
DP-1
y=
DP-1
Pz =
Dz.
in short: dz/dt =
Dz.
But we know how to solve the diagonal system dz/dt= Dz for z. Then from this solution z we derive the solution to the original system dy/dt = Ay given by y = Pz.
Algorithm for solving a first order linear differential
system
dy/dt = Ay
[if A is a diagonalizable n x n matrix]:
Write A = PDP-1
for P invertible and
D diagonal.
Solve the system dz/dt = Dz,
and set y = Pz..
Example
Example: Here is one time when we will use complex eigenvalues. Consider the system
dx/dt = ky, dy/dt =-kx
for k a positive integer; let us consider the general initial conditions
x(0) = a, y(0)= b.
(Notice that, automatically, dx/dt(0) =kb and dy/dt(0) = -ka.) The corresponding linear system has the form
![]()
The matrix A has no real eigenvalues, but has the distinct complex eigenvalues +ik and -ik (for i the square root of -1). If we work with the complex entries in the usual fashion (and all we really need to know is that i2 = -1), it is easy to find eigenvectors corresponding to these eigenvalues, and for instance we can take as the matrix of eigenvectors
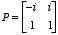 , with
, with
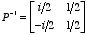 .
.
Now we have
![]() and then
and then
![]() , while
, while
![]() .
.
It follows (assuming we can exponentiate in the complex case in the same way that we can in the real case) that
w(t) = {(ia+ b)/2}eikt and z(t) = {(-ia + b)/2}e-ikt.
Finally,
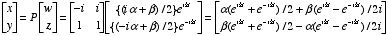 .
.
Of course, from one variable calculus we also know that the pair
x(t) = acoskt + bsinkt, y(t)= bcoskt - asinkt
also satisfies the original set of equations and side conditions. A
comparison of these two versions of the solution to the problem
reveals a remarkable connection between complex exponentiation and
the trigonometric functions (Euler's formula):
Comment: For a proof of Euler's formula, compare the Maclaurin expansions of eix, cos x, and sin x.