![]()
Although Gaussian elimination provides us with a way of checking whether a matrix is invertible, an older method exists as well: it produces a remarkable number called the determinant: if this number is invertible (nonzero), this means that the matrix is invertible, while if it is not invertible (zero!), this means that the matrix is not invertible. Moreover, the calculation of this "determinant" for the matrix and for certain related matrices allows the computation of the inverse in the invertible case. These calculations are more expensive in terms of computation time than the ones based on Gaussian elimination and other methods, so they are not used much for explicit computation. But these calculations do allow important additional features of matrices to be discerned, including other applications than just the solution of linear systems of equations, and so remain important in practice, not just in theory. Furthermore, the same number is needed for the change of variables formula in multivariable calculus!
Def. The determinant of a 2 x 2 matrix A:
![]()
is the scalar (ad - bc). It is denoted det A.
Examples
Example: For the general 2 x 2 matrix as above, if a is different from zero, we can clearly use Gaussian elimination to find that the matrix has rank 2 if and only if (d - bc/a) is different from zero; if c is different from zero, then the matrix has rank 2 if and only if (b - da/c) is different from zero, and if both a and c are zero, then the matrix clearly has rank less than 2. But this information means that the matrix is invertible if and only if (ad - bc) is different from zero.
Example: Find all numbers c such that the matrix
![]()
is invertible.
We want to define determinants for larger square matrices as well. (By the way, for the 1 x 1 case, we define the determinant of [a] to be a, and then clearly the 1 x 1 matrix is invertible if and only if its determinant is nonzero.) It is possible to define the determinant of a larger matrix in terms of the determinants of related matrices, the next size smaller. (In computer science, this is called a recursive procedure; mathematicians call it an inductive definition.)
Notation
If A is an n x n matrix, n
> 2, the matrix
Aij
denotes the (n -1) x (n - 1) matrix obtained
from A by deleting row i
and column j.
Definition by Induction:
If the determinant has
been defined for (square)
matrices of size (n -1) x (n - 1),
for some n> 2, then the determinant
of an n x n matrix A =
[a ij]
is defined to be
(-1)2 a11 det A11 + (-1)3 a12 det A12 + · · · + (-1)1+n det A1n.
The numbers (-1)(i+j) det A ij are called the (i,j) cofactors of A, and the formula above is called the cofactor expansion of A, along the first row.
Examples
In fact, we do not have to compute the cofactor expansion using the first row: any row will do. If a matrix has a row with many zeros, this simplifies the computation.
Theorem If A is an n x n matrix, then for any i with 1 < i < n we have
det A = ai1 ci1 + · · · + ain cin,
with cij = (-1)(i+j) detAij the (i,j) cofactor of A.
This result can be established by using the inductive definition of determinant to derive an explicit formula for the determinant as a sum of products of entries of the original matrix. It is easily seen that each entry in the sum is a product of n entries, selected one from each row and one from each column of the original matrix, along with a somewhat mysterious factor of ±1. depending on the location of the entries, and that the sum ranges over all such possible choices of products of n entries, subject to those constraints. The choice of a different row in the cofactor expansion merely indicates a way of reducing this sum of products to one involving products of pairs involving single entries from A (the aij), and products of (n - 1) terms along with the factors ±1 (the cij) from the matrices one size smaller.
Examples
An important example of the use of this result is the computation of the determinant of an upper or lower triangular square matrix.
Theorem The determinant of an upper or lower triangular m x n matrix is the product of the entries on its diagonal.
Indeed, for a lower triangular matrix this result is easily seen by using the cofactor expansion along the top row: the only nonzero term results from the determinant of the matrix with the first row and column deleted, which is a smaller lower triangular matrix. Repeated applications of this procedure yield the result. For upper triangular matrices, the cofactor expansion along the bottom row yields a similar argument.
Examples
Geometric Application: Area of a Parallelogram
Given two vectors in
R2,
say
![]()
we can consider the parallelogram they determine (if they are not parallel). If, for instance, both of the vectors are in the first quadrant, and a > b and c < d, we can rotate the parallelogram clockwise through the angle q which u makes with the positive x-axis to simplify the problem. If we set h 2 = a 2 + c 2 , then cosq = a/h, sinq= c/h, and the rotation matrix for this clockwise rotation is R-q. Then
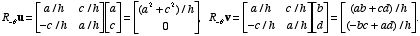
The area of a parallelogram is the product of its base length and its height, which for the rotated version is then clearly ((a 2 + c 2 )/h)((-b c + ad)/h) = ad - bc. This value is the determinant of the matrix [u v]. If the order of the vectors had been reversed, the determinant would have been negated, while the area would not have been changed. It follows easily that, in general, the area of the parallelogram in R2 determined by the vectors u and v is |det[u v]|. This statement also makes sense if the vectors are parallel, since in that case they generate a parallelogram that can be considered as having zero height, and the resulting determinant is also zero.
Similar arguments apply in three dimensions, and it turns out that the volume of the parallelepiped generated by a triple of vectors u, v, w in R3 is exactly |det[u v w]|. We also have a natural definition for the volume of a parallelepiped in even higher dimensions n: the volume of the parallelepiped generated by an n-tuple of vectors v1, . . ., vn in Rn is taken to be |det[v1 . . . vn]|.