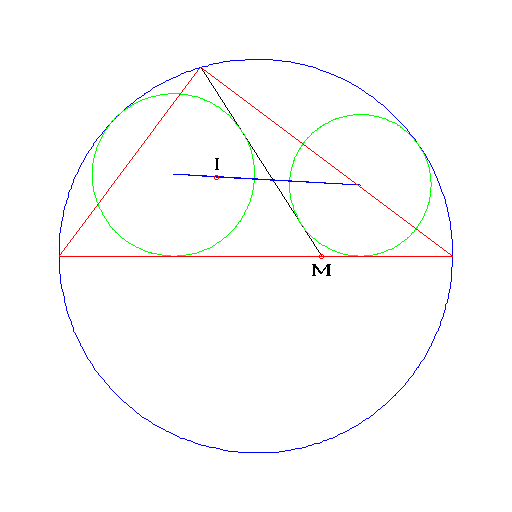
Thebault's Theorem

Thebault:=proc() local m,n,t,p1,p2, I1,T,A,M,eq1,eq2,lu,Ci,Ci1,i,j,SOL,lua:
T:=Te(m,n): A:=T[3]:
I1:=Incenter(m,n): M:=[t,0]:
Ci:=Ce(T): Ci1:=(x-p1)^2+(y-p2)^2-p2^2:
eq1:=TouchCeLe1
(Ci1,Ci): lu:=solve(eq1,p2):
if subs({m=1/3,n=1/3,t=1/2,p1=1/2},lu[1])>0 then lu:=lu[1]: else
lu:=lu[2]: fi:
eq2:=TouchCeLe1
(Ci1,Le(A,M)):
eq2:=numer(normal(subs(p2=lu,eq2))):
for i from 1 to nops(SOL) do
for j from i+1 to nops(SOL) do
if Colinear(I1,SOL[i],SOL[j]) then
RETURN(true): fi:
od:od:
false:
end:
lua:=solve(eq2,p1):
SOL:=[seq([lua[i], subs(p1=lua[i],lu)],i=1..nops([lua]))]: