Mathematical Physics

No attempt will be made here to explain what mathematical physics is about. There is no general agreement even among the experts. Moreover, this field of research is regarded as somewhat dubious by many physicists. However, the following words of Maxwell are right on target:

• The first processes, therefore, in the effectual studies of the sciences, must be ones of simplification and reduction of the results of previous investigations to a form in which the mind can grasp them.

  J.C. MAXWELL
  On Faraday's lines of force

Foundations of Quantum Mechanics

Nobody has explained why we should worry about the foundations of quantum mechanics better than John Bell:

• ... conventional formulations of quantum theory, and of quantum field theory in particular, are unprofessionally vague and ambiguous. Professional theoretical physicists ought to be able to do better. Bohm has shown us a way.

  J.S. BELL
  Speakable and Unspeakable in Quantum Mechanics

• It would seem that the theory [quantum mechanics] is exclusively concerned about "results of measurement", and has nothing to say about anything else. What exactly qualifies some physical systems to play the role of "measurer"? Was the wavefunction of the world waiting to jump for thousands of millions of years until a single-celled living creature appeared? Or did it have to wait a little longer, for some better qualified system ... with a Ph.D.? If the theory is to apply to anything but highly idealized laboratory operations, are we not obliged to admit that more or less "measurement-like" processes are going on more or less all the time, more or less everywhere. Do we not have jumping then all the time?

  The first charge against "measurement", in the fundamental axioms of quantum mechanics, is that it anchors the shifty split of the world into "system" and "apparatus". A second charge is that the word comes loaded with meaning from everyday life, meaning which is entirely inappropriate in the quantum context. When it is said that something is "measured" it is difficult not to think of the result as referring to some preexisting property of the object in question. This is to disregard Bohr's insistence that in quantum phenomena the apparatus as well as the system is essentially involved. If it were not so, how could we understand, for example, that "measurement" of a component of "angular momentum" ... in an arbitrarily chosen direction ... yields one of a discrete set of values? When one forgets the role of the apparatus, as the word "measurement" makes all too likely, one despairs of ordinary logic ... hence "quantum logic". When one remembers the role of the apparatus, ordinary logic is just fine.

  In other contexts, physicists have been able to take words from ordinary language and use them as technical terms with no great harm done. Take for example the "strangeness", "charm", and "beauty" of elementary particle physics. No one is taken in by this "baby talk". ... Would that it were so with "measurement". But in fact the word has had such a damaging effect on the discussion, that I think it should now be banned altogether in quantum mechanics.

  J.S. BELL
  Against "Measurement"

Bohmian Mechanics

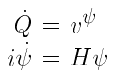
Bohmian mechanics is the most naively obvious embedding imaginable of Schrödinger's equation into a completely coherent physical theory. It describes a world in which particles move in a highly non-Newtonian sort of way, one which may at first appear to have little to do with the spectrum of predictions of quantum mechanics. However, this deterministic theory of particles in motion completely accounts for all the phenomena of nonrelativistic quantum mechanics, from spectral lines to interference effects, and it does so in a completely ordinary manner. It was first presented in 1927 by Louis de Broglie, just after the inception of quantum mechanics itself. It was soon abandoned and utterly ignored until rediscovered a quarter century later by David Bohm, who showed how it resolved the measurement problem and accounted for the reduction of the wave packet. Its principal advocate for the past three decades was John Bell:

• Is it not clear from the smallness of the scintillation on the screen that we have to do with a particle? And is it not clear, from the diffraction and interference patterns, that the motion of the particle is directed by a wave? De Broglie showed in detail how the motion of a particle, passing through just one of two holes in screen, could be influenced by waves propagating through both holes. And so influenced that the particle does not go where the waves cancel out, but is attracted to where they cooperate. This idea seems to me so natural and simple, to resolve the wave-particle dilemma in such a clear and ordinary way, that it is a great mystery to me that it was so generally ignored.

  J.S. BELL
  Speakable and Unspeakable in Quantum Mechanics

• ...in physics the only observations we must consider are position observations, if only the positions of instrument pointers. It is a great merit of the de Broglie-Bohm picture to force us to consider this fact. If you make axioms, rather than definitions and theorems, about the "measurement" of anything else, then you commit redundancy and risk inconsistency.

  J.S. BELL
  Speakable and Unspeakable in Quantum Mechanics

For a little more on Bohmian mechanics click here; for more detail, click here.

*The picture of the two-slit interference patterm is courtesy of Martin Daumer*

Back to the home page of Sheldon Goldstein