
Here is the problem:
Theoretical results imply that x+3yz has a maximum and a minimum on the sphere x2+y2+z2=1. Use Lagrange multipliers to find these maximum and minimum values.

Here is a picture of x+3yz=.5 and
x2+y2+z2=1. The .5 is a random value
of the constant. This
hyperboloid divides the sphere into two pieces. On one piece of the
sphere, the function x+3yz has values larger than .5, and on the
other piece, the values of the function are less than .5.
The picture uses display3d with
ϑ=80 and φ=−75 to show two graphs combined. The graphs
are the results of the following implicit3d commands for the sphere and
hyperboloid respectively. The numpoints=1800 option increases the
number of points sampled from the default of 1000. With only 1000
points, the graphs drawn for the surfaces look very polyhedral. That
is, they resemble more closely linear approximations to the true
smooth graphs.
implicitplot3d(x^2+y^2+z^2=1,x=-2..2,y=-2..2,z=-2..2,axes=normal,numpoints=1800,color=blue);
implicitplot3d(x+3*y*z=.5,x=-2..2,y=-2..2,z=-2..2,axes=normal,numpoints=1800,color=green);
In this specific case, we want to solve these equations
1= λ(2x)
3z=λ(2y)
3y=λ(2z)
1=x2+y2+z2
> f:=x+3*y*z;
f := x + 3 y z
> g:=x^2+y^2+z^2;
2 2 2
g := x + y + z
> eqx:=diff(f,x)=L*diff(g,x);
eqx := 1 = 2 L x
> eqy:=diff(f,y)=L*diff(g,y);
eqy := 3 z = 2 L y
> eqz:=diff(f,z)=L*diff(g,z);
eqz := 3 y = 2 L z
> sols:=solve({eqx,eqy,eqz,g=1});
sols := {y = 0, x = 1, L = 1/2, z = 0}, {y = 0, x = -1, L = -1/2, z = 0},
{L = 3/2, x = 1/3, y = 2/3, z = 2/3},
{L = 3/2, x = 1/3, y = -2/3, z = -2/3},
{L = -3/2, x = -1/3, y = 2/3, z = -2/3},
{L = -3/2, x = -1/3, y = -2/3, z = 2/3}
> values:=seq(subs(sols[j],x+3*y*z),j=1..nops({sols}));
values := 1, -1, 5/3, 5/3, -5/3, -5/3
L is used instead of λ. The solve step finds all solutions of the system
of equations. Finally, the command values:=... substitutes the values found into
the constraint function. Inside, the nops({sols}) instructs Maple to count the number of elements in the
set of solutions -- that is, the number of solutions to the Lagrange
multiplier equations. Then Maple will
substitute each of these solutions, in
order, into the constraint function.

Therefore we have learned that the maximum value of the objective function is 5/3. This value is attained at exactly two points: (1/3,2/3,2/3) and(1/3,–2/3,–2/3). The minimum value of the objective function is –5/3, and this is attained at the two points (–1/3,2/3,–2/3) and (–1/3,–2/3,2/3).
A picture of the constraint surface with the level surface corresponding to constant=5/3 is shown to the right. The two points of tangency shown are the points found by the Lagrange multiplier method.
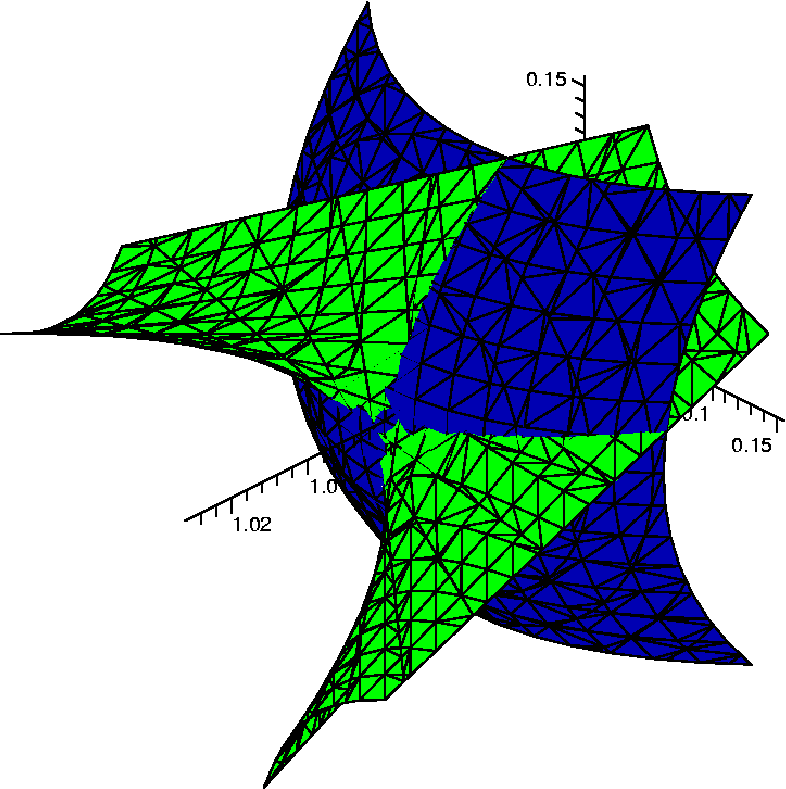 A graph of the constraint and the level surface x+3xy=1 near the point
(1,0,0) is shown to the right. The window was chosen with some care,
since the features here are quite delicate: x is between .975 and
1.025 and y and z are both in the interval [−.15,.15]. The two
surfaces are tangent, but the constraint surface is locally both
inside and outside of the sphere -- that is, the function x+3yz has
both larger and smaller values than constant=1 on
x2+y2+z2=1 near (1,0,0). The
objective function when restricted to the constraint surface near
(1,0,0) therefore has saddle behavior.
A graph of the constraint and the level surface x+3xy=1 near the point
(1,0,0) is shown to the right. The window was chosen with some care,
since the features here are quite delicate: x is between .975 and
1.025 and y and z are both in the interval [−.15,.15]. The two
surfaces are tangent, but the constraint surface is locally both
inside and outside of the sphere -- that is, the function x+3yz has
both larger and smaller values than constant=1 on
x2+y2+z2=1 near (1,0,0). The
objective function when restricted to the constraint surface near
(1,0,0) therefore has saddle behavior.
|
Change the objective function slightly: don't throw things away, but be careful! |
Suppose we keep the unit sphere
x2+y2+z2=1 as constraint, and
consider the objective function f(x,y,z)=x+.5yz (the 1 in front of yz
has been changed to .5). What follows is true for x+kyz if
0≤k≤1, but keeping track of the results for one value of k will
be complicated enough!

The maximum value of this f on the unit sphere is 1, and this value occurs only at the point (1,0,0). The minimum value is −1, which occurs only at the point (−1,0,0). A picture of the constraint surface and the level surface of the objective function which corresponds to the maximum value, the graph of x+.5yz=1, is shown to the right.
Algebraically, this is a solution to the Lagrange multiplier equations which has both y=0 and z=0. This sort of solution is exactly one which may be thrown away when people compute "by hand".
Here is a sequence of Maple commands similar to what was just done. We only display the results of the last command. This should give the values of the objective function which result. The extreme values should be among these "candidates".
> f:=x+.5*y*z:
> g:=x^2+y^2+z^2:
> eqx:=diff(f,x)=L*diff(g,x):
> eqy:=diff(f,y)=L*diff(g,y):
> eqz:=diff(f,z)=L*diff(g,z):
> sols:=solve({eqx,eqy,eqz,g=1}):
> values:=seq(subs(sols[j],x+.5*y*z),j=1..nops({sols}));
values := 1., -1., 1.250000000, 1.250000000, -1.250000000, -1.250000000}
The values which Maple returns as
candidates for extreme values are ±1 and ±1.25.

To the right is a graph of the unit sphere and the surface x+.5yz=1.25, at an angle similar to what was just shown before. The surface for the candidate "extreme value" does not seem to touch the unit sphere! What happened?
Maple is a computer program. It will try to do exactly the computations requested by the user.
Be careful!
Let's show a bit more information about by looking in detail at the result of one of the intermediate steps, the solve command.
> sols:=solve({eqx,eqy,eqz,g=1});
sols := {z = 0., x = 1., y = 0., L = 0.5000000000},
{z = 0., y = 0., x = -1., L = -0.5000000000},
{x = 2., L = 0.2500000000, z = 1.224744871 I, y = 1.224744871 I},
{x = 2., L = 0.2500000000, z = -1.224744871 I, y = -1.224744871 I},
{x = -2., z = 1.224744871 I, y = -1.224744871 I, L = -0.2500000000},
{x = -2., y = 1.224744871 I, z = -1.224744871 I, L = -0.2500000000}
The third element of sols isHere is a quote from a Maple help page. It is an important part of the design of Maple which should be known to every user:
| By default, Maple performs computations under the assumption that the underlying number system is the complex field. |
So, for example, we have:
> solve(x^2+1);
I, -I
We can change this default setting. In the
case of computations with Lagrange multipliers such a change is
useful. Consider the following commands and responses.
> with(RealDomain):
> solve(x^2+1);
> sols:=solve({eqx,eqy,eqz,g=1});
sols := {z = 0., x = 1., y = 0., L = 0.5000000000},
{z = 0., y = 0., x = -1., L = -0.5000000000}
> values:=seq(subs(sols[j],x+.5*y*z),j=1..nops({sols}));
values := 1., -1.
When the RealDomain package is
loaded, Maple declares that
x2+1=0 has no roots. It also discards any elements of sols which have non-zero imaginary
parts, and so it declares as a result of the substitution step, only those values
which correspond to real solutions of the Lagrange multiplier
equations. We don't get the outputs ±1.25 because the
intermediate steps involved imaginary numbers which RealDomain discards. Those solutions
won't be geometrically valid.
Maintained by greenfie@math.rutgers.edu and last modified 3/3/2010.