∫LeftRight[Top(x)–Bot(x)]dx.
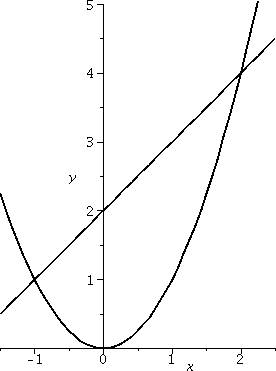
| Thursday, December 10 | (Lecture #28) |
|---|
Area between two curves
Here's the final topic of the semester, which is a simple introduction
to the uses of the definite integral. The definite integral has
hundreds of important applications in science and engineering.
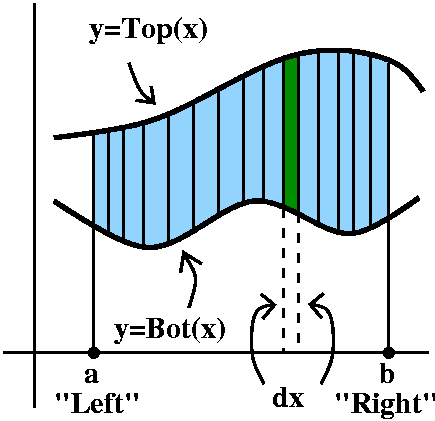
Suppose we are given two functions defined on an interval, Top(x) and Bot(x) ("Bot" is an abbreviation for "Bottom") and we know on that interval that Top(x)>Bot(x). How can we compute the area enclosed by the two curves and by vertical lines on the sides of the interval?
I always imagine that the interval is chopped into lots of little
pieces, each of length dx. Then these pieces chop up the area, as
shown in the picture to the right. Each little slice of area is
almost a rectangle (if we ignore the possible tilts at the top
and bottom). The area of the approximate rectangle is [Top(x)–Bot(x)]
(the length of the vertical side, the difference in the heights of the
graphs) multiplied by dx, the width. Now I need to take the Sum of these approximating slices, and add them
up from a to b, or, as I think, from Left to Right. Therefore I believe that the area between these curves on this interval is
∫LeftRight[Top(x)–Bot(x)]dx.
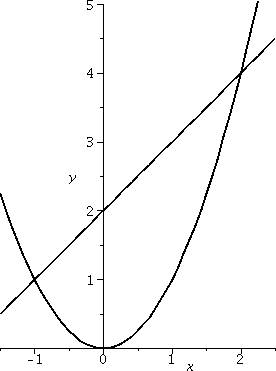
Random example #1
This example is not random, but it is constructed so I could do it
easily in class. I would like to find the area of the region enclosed
by the line y=x+2 and the parabola y=x2. I would probably
try to begin almost any problem of this type by sketching the region
first. The picture to the left is such a sketch. Where do these curves
intersect? Well, we need to find x's which give the same y, so we
solve x2=x+2 so that x2–x–2=0 and this is (wow!
Oh, hold on, he made it so it would work out) x2–x–2=0 so
that (x–2)(x+1)=0. The roots are x=2 and x=–1.
I honestly think that the phrase "the region enclosed
by the line y=x+2 and the parabola y=x2" specifies exactly
one piece of the plane. You can argue with me -- I discuss this a bit
more in the example below. Here I think we have Left=–1 and Right=2
and Top(x)=x+2 and Bot(x)=x2. So let's compute:
∫LeftRight[Top(x)–Bot(x)]dx=∫–12[{x+2}–{x2}]dx=
(1/2)x2+2x–(1/3)x3|–12=[(22/2)+2·2–(8/3)]–[((–1)2/2)+2·(–1)–(–8/3)].
This turns out to be 9/2. I hope. And, by the way, if you look at the
picture, I hope you can see that the region fits inside a box with
height 4 and width 3, so the area should be less than 3·4=12,
which it is. Getting some approximate idea of the answer is useful, if
you, like me, make sign errors and ... well, other kinds of errors.
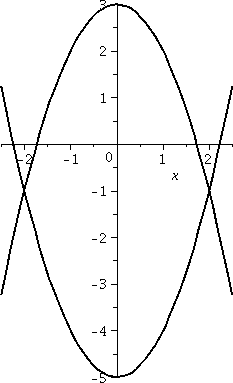 Random example #2
Random example #2
Again, this is an arranged example and everything will work out
neatly. Real problems are rarely like this. I'd like to compute the
area of the part of the plane which is between the parabolas
y=x2–5 and y=3–x2. The first curve opens
up and has its bottom at (5,0). The second opens down, with its
top at (3,0). A picture of the two curves is shown to the right.
I mentioned in class that it is certainly possible to "misunderstand" the statement of this problem, if you work at it. The plane is actually divided into five different regions by these two curves. And maybe someone could maybe declare that there's more than one candidate for the region between the parabolas (maybe all five are candidates, or maybe only three of them are?). I guess maybe I might agree if you really argue with me about it, but if the discussion is just a way to get out of computing the area of the only region with finite area then I would not agree. Please compute the area of that region, and then, later, argue about it.
The curves intersect where x2–5=3–x2. Since this is a problem in a math class, let's see: that's 2x2=8 or x2=4 so that x=+/–2. I think that Left=–2 and Right=+2.
Something new!?
There is a little bit that's new here. Notice that if
Top(x)=3–x2 and Bot(x)=x2–5, then actually
Bot(x) is always negative in the interval [–2,2]. Even so, the
quantity Top(x)–Bot(x) gives the geometric length
of the vertical side of a (dx) thin slice of area. Top(x)–Bot(x) will
be positive. In fact, if you look really carefully at the picture,
you'll see that there are two pieces of [–2,2] where both
Top(x) and Bot(x) are negative. But Top(x) is still bigger than
Bot(x), so Top(x)–Bot(x) will be positive, even though both of them
are negative. The geometric length is still Top(x)–Bot(x).
The computation
∫LeftRight[Top(x)–Bot(x)]dx=∫–22[{3–x2}–{x2–5}]dx=
∫–22[{8–2x2]dx=8x–(2/3)x3|–22=[(8·2)–(2/3)23]–[(8·–2)–(2/3)(–2)3]=64/3.
This is less than a box which is 8 units high and 4 units wide (such a
box would enclose the entire area). Also, several students remarked
that we could have computed the integral from 0 to 2 and doubled the
result, to take advantage of symmetry.
Random example #3
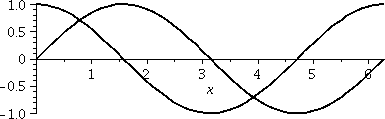 I would like to find the geometric area between the sine and
cosine curves over one period of these functions. So I drew a
picture similar to what's shown to the right. Again, it may be
possible to misunderstand the question since this situation is more
complicated than previous ones. But "one period" is 2Π here, and the
word "between" in this situation refers, in fact, to three specific
regions in the picture.
I would like to find the geometric area between the sine and
cosine curves over one period of these functions. So I drew a
picture similar to what's shown to the right. Again, it may be
possible to misunderstand the question since this situation is more
complicated than previous ones. But "one period" is 2Π here, and the
word "between" in this situation refers, in fact, to three specific
regions in the picture.
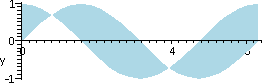 So the area which I wanted to compute is shown to the right. Here is
what I thought that I needed to do (clear evidence that the brain was
not totally functional!). I thought that I would need to split the
area computation into three pieces, and compute three different
integrals, and then add them up. The idea would be as shown to the
left
So the area which I wanted to compute is shown to the right. Here is
what I thought that I needed to do (clear evidence that the brain was
not totally functional!). I thought that I would need to split the
area computation into three pieces, and compute three different
integrals, and then add them up. The idea would be as shown to the
left
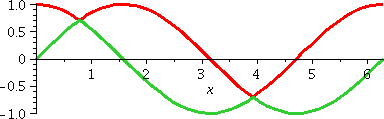 where first one formula then the other, and then the other again, is
on top. Well, this could be done but it would actually be much more
work than is needed.
where first one formula then the other, and then the other again, is
on top. Well, this could be done but it would actually be much more
work than is needed.
A student (who?) kindly pointed out that the left-most region and the right-most region when put together are congruent to the central region: so the sum of the areas of these two regions must be equal to the area of the region in the middle. Thank you!
The curves intersect where sin(x)=cos(x). This is at x=Π/4 and
x=5Π/4. So Left=Π/4 and Right=Π/4 and between these numbers, the
sine curve will be Top(x) and the cosine curve will be Bot(x). So I
need to compute twice the definite integral over this interval
to get the total area requested. Here we go (and be careful with minus
signs!):
2∫Π/45Π/4(sin(x)–cos(x))dx=–cos(x)–sin(x)|Π/45Π/4=[–cos(5Π/4)–sin(5Π/4)]–[–cos(Π/4)–sin(Π/4)]=
[–{–sqrt(2)/2}–{–sqrt(2)/2}]–[–{sqrt(2)/2}–{sqrt{2}/2}]=4sqrt(2)
There were only SEVEN minus signs
in the next-to-last expression. Mistakes are easy!
Another ...
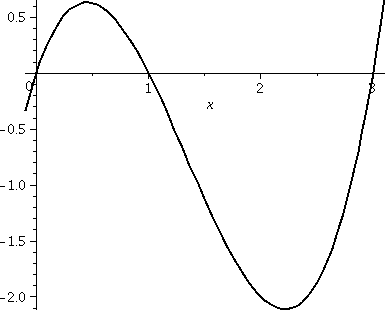
How much geometric area is enclosed by y=x(x–1)(x–3) and the
x-axis? Again, a graph is shown to the right, and these bumps
definitely have different sizes. But my patience
(?) is running out. In a spare tenth of a second, we get:
> int(x*(x-1)*(x-3),x=0..1);
5/12
> int(x*(x-1)*(x-3),x=1..3);
-8/3
So the geometric area is 5/12+8/3, which is, I can tell you, 37/12. So
this is ∫03|x(x–1)(x–3)|dx (the absolute value signs make both bumps "sit" on
top of the x-axis. I did compute these integrals in class, and the
first step was multiplying out x(x-–1)(x–3) so I could get
the antiderviative easily.
|
Sideways? I asked what does the curve defined by the equation (y–1)(y–2)=x look like? With a bit of thought, we decided that it was a parabola with axis of symmetry parallel to the x-axis, and that it was opening to the right. A graph is shown to the right. Notice, please, that the point (2,0) is on the graph, as well as the point (0,2). Therefore there's a (exactly one!) straight line through these two points. Its equation is x+y=2 (Admission: I sort of guessed at the equation, since the sum of each pair of coordinates is 2, that must be the equation!). What's the area of the region bounded by the line and the parabola? | 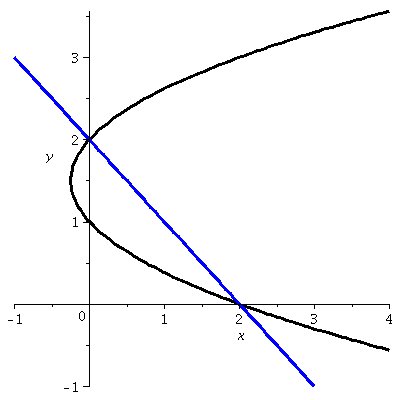 |
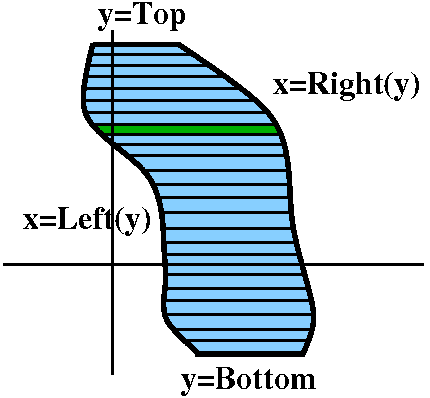 The dy method
The dy method
If we have a region in the plane bounded by two curves, x=Left(y) and
x=Right(y) (where Left(y)<Right(y) for the y's of interest here)
and also bounded by lines y=Bottom and y=Top, then we could imagine
slicing this area by lots of horizontal lines dy apart. The region
would be divided into lots of pieces, and each piece would
approximately be retangular. The height of the (almost) rectangle
would be dy, and the width would be Right(y)–Left(y). So the area
would be (Right(y)–Left(y))dy. Since this is the area of a slice, we would get
the total area by taking the Sum of
the areas of the slices, from the Bottom to the Top:
∫y=Bottomy=Top(Right(y)–Left(y))dy.
In our case ...
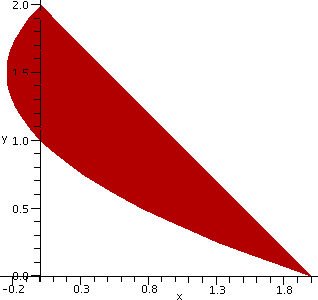 Top is 2 and Bottom is 0. Left(y) is (y–1)(y–2)=y2–3y+2
(you should multiply/distribute/expand/foil whatever! before
integrating) and Right(y) is 2–y. Thus the area can be computed by
Top is 2 and Bottom is 0. Left(y) is (y–1)(y–2)=y2–3y+2
(you should multiply/distribute/expand/foil whatever! before
integrating) and Right(y) is 2–y. Thus the area can be computed by
∫y=Bottomy=Top(Right(y)–Left(y))dy=
∫y=0y=2([2–y]–[y2–3y+2])dy=
∫y=0y=2([2y–y2])dy=y2–(1/3)y3|02=4–8/3=4/3.
Comments
Certainly this is not the only method of getting this area. You could
possibly imagine dissecting the area dx, and chopping it up
somehow so the computation could be done. You would need to solve for
x in terms of y, which is possible in this case but maybe not too easy
if the equation were more complicated. Also that would be much more
work, I think. Or maybe you just interchange x and y, and then redraw
the graph, and do it dx. That's certainly possible. I just report,
though, that for many students in the class (physics students,
engineering students) many other geometric and physical quantities
will occur (moment of inertia, center of gravity, etc.) which can be
computed more naturally dy, and therefore "chopping up" regions in
this way will be useful.
Winding up ...
Please study for the final exam.
| Tuesday, December 8 | (Lecture #27) |
|---|
The derivative of 17x is (ln(17))17x. And the derivative of 556x is (ln(556))556x. The derivative of x400400x is 400x399400x+x400(ln(400))400x. The derivative of 37sec(5x2) is (ln(37))37sec(5x2)sec(5x2)tan(5x2)10x.
All this was preparation for understanding the solutions to a differential equation and for manipulating these solutions, using ln and exp.
What are the solutions?
I would hope that dy/dt=ky would have a family of solutions
(the general solution) and we would use an initial condition to pick
out one of these (the particular solution).
Well, first let's guess one solution of dy/dt=ky. For example,
I know a wonderful function which is its own derivative: the
exponential function (so that's a solution when k=1). After some
further consideration, we could try the function
ekt. Indeed, if we differentiate this, the Chain Rule
"spits out" a multiplicative factor of k, so the derivative of
ekt is ektk, and this is ky.
Are there other solutions? Here is a trick to learn about other
possible solutions. It is a fairly clever trick, and is used in other
computations, which is why I'm showing it to you. Suppose y is
another solution of dy/dt=ky. I want to compare it to
the solution we know, ekt. The trick is to compare this
way:
Look at y/ekt (the unknown solution y divided by the known
solution, ekt). Let's differentiate this. The Quotient Rule
gives us:
y´(ekt)–y(ektk)
-------------------
(ekt)2
Look carefully at the top of the fraction. We are assuming
that y´ is ky. Then the top becomes:
y´(ekt)–y(ektk)=ky(ekt)–y(ektk)=0
because things exactly cancel. This means (MVT tells us: a function
with 0 derivative is constant) y/ekt is a
constant, C. So y=Cekt.
Cekt
I admit totally truthfully that I don't go through any process
remotely like what I just showed you in practice. In fact, if I think
that the differential equation dy/dt=kt is a good description of a
situation, then I immediately jump to Cekt. If you work
with such situations for a while, I think you will do this also.
Student-suggested bacteria
We got some bacteria with the
following (hypothetical) observations of a bacterial colony (I forget
the actual numbers we used in class so I will just invent some here):
Initially, there are 50 bacteria. In 3 hours, 100 bacteria are observed (3 hours is called the doubling time). In 6 hours, 200 bacteria are observed.People believe that dy/dt=kt is a differential equation which appropriately describes growth in such a situation (some comments on this assumption are below!) because bacteria (generally) reproduce asexually by division, and new bacteria are created by a fraction of the current bacteria splitting. I would like to make a mathematical model (in this case, get a simple formula) for the bacteria at time t.
I will measure t in hours from the start of the observation. B(t) will be the number of bacteria at time t. So B(0)=50 and B(3)=100 and B(6)=200. If we suppose that B(t)=Cekt (that follows from the differential equation's applicability to this situation) then we need to identify numbers for C and k.
Since B(0)=50 and B(0)=Cek·0=Ce0=C·1=C. So C is 50. Now we know that B(t)=50kt. We need to identify k, and we can use B(3)=100 for this. So: 100=50ek(3) which is 2=e3k which is (take ln's!) ln(2)=3k so that k=[ln(2)/3]. (People who work with these equations a great deal develop lots of computational shortcuts!)
So the number of bacteria is given by
B(t)=50e[ln(2)/3]t. We could check this formula by plugging
in t=6, since we know the answer should be 200. Here:
B(6)=50e[ln(2)/3]6=50e2ln(2)=50eln(4)=50·4=200
(because exp and ln are inverse functions).
Defects of the model?
Maybe bacteria don't reproduce the way we think (indeed, when I was
younger, mostly people did believe bacteria could only reproduce
asexually, but this is not always true). There's a more subtle
assumption hidden in the model. The exponential function grows very fast. For example, there will be
1010 bacteria in about 82 hours (I did these computations
secretly). That isn't so big, biologically, since there may be about
1014 cells in the human body. But if you continue to
believe this model is valid, there will be 10100 bacteria
after about five and a half weeks. Now to understand 10100
is difficult. Uh ... there are about, say, 6 billion people in the
world, and so there are about
6·109·1014=6·1023
human cells in the world. Multiplied exponentials add
"upstairs". This means we'd need lots and lots of worlds (more than
1075) to have maybe one bacteria per cell.
In fact, the bacteria will grow exponentially as long as conditions allow. That is, there needs to be adequate food, places to excrete poisons, etc. I think, in reality, these limits to growth impose themselves in a realistic way fairly soon in the case of bacterial growth. So the exponential model for bacterial growth is valid, but really only for relatively brief intervals. Exponential decay (with k<0) can be applied more appropriately over long periods of time to radioactivity. I'll try to discuss this next time.
Exponential growth: a textbook problem
This is problem #16 of section 5.8: An insect population triples in
size after 5 months. Assuming exponential growth, when will it
quadruple in size?
I added the following question:
What is the doubling time of this type
of insect?
Solution
The phrase "Assuming exponential growth" means that, if B(t) gives
the number of bugs at time t, then we should assume that B(t)=Cekt.
So (units!) B(t) will represent the population of the insects at time t measured in months since the start. We know that B(0)=Ck·0=C and
B(5)=3C. So 3C=Cek·5, and if we divide by C and ln both sides and divide by 5, we get k=ln(3)/5.
So B(t)=Ce[ln(3)/5]t and we want to know when the
population quadruples, that is, reaches 4C. (By the way, it is a good
idea to have some estimate in mind just so we can check the answer,
or, if the answer is correct and way off the estimate, we can improve
estimating skills. In this case, I would guess that about
another month or so is needed to get to four times the initial
population: so my guess is 6, maybe a little bit more.) So let's solve
4C=Ce[ln(3)/5]t: we divide by C, ln both sides, and divide
by [ln(3)/5]. The result is t=[5ln(4)/ln(3)]≈6.31 months.
I had also asked "What is the doubling time?" Doubling time is a standard measure of growth, and is the time needed for the population to double (indeed!). If the formula governing growth rate is exponential, then doubling time is a constant (hey, if the population was given by t2+1, then the population doubles from 0 to 1, and it also doubles from 1 to sqrt(3): the time intervals change!). In this case, we are told that population is given by an exponential formula and that a population quadruples in 6.31 months. I think the doubling time is 3.15 months.
Exponential decay: a textbook problem
This is problem #17 of section 5.8: A 10-kg quantity of a radioactive
isotope decays to 3 kg after 17 years. Find the decay constant of the
isotope.
I added the following questions:
Also, what's the half-life? What is half-life?
Solution
Well, suppose R(t) is the quantity in kg of the radioactive substance
at time t in years. We assume (and mostly this is true) that amount of
the substance is given by R(t)=Cekt. We know that R(0)=10,
so that C=10 (always try to start the "clock" in these problems at 0
so that C will be the initial amount). Also since R(17)=3,
10ek·17=3. Now divide by 10, ln both sides and
divide by 17: k=ln(3/10)/17. I think this is the decay
constant. Please notice that since 3/10 is less than 1, ln(3/10) is
negative so the constant in the exponential formula is
negative, and this is, indeed, decay.
The half-life of a radioactive substance is the time needed for
an initial quantity to reduce to half. Since we are told that in 17
years, 10 kg reduces to 3 kg, I am sure that a half-life of this
substance will be less than 17. In fact, a half-life will be more
than, say, 8, since a half-life of 8 would result in 2.5 kg at 16. So
a casual estimate of half-life is somewhere between 8 and 17.
Here we want t so that 10e[ln(3/10)/17]t=5. Divide by 10,
take lns, and divide by [ln(3/10)/17]: the result is
t=ln(1/2)/[ln(3/10)/17]. This is about 9.79.
Radioactivity: a very short discussion
There are lots of radioactive isotopes. A web page I found mentions
these "widely used industrial isotopes ... 192Iridium with
a half-life of 74 days ... and 60Cobalt with a half-life of
5.3 years". If radioactive substances have the same activities (there
are three principal types: alpha and beta particle emissions and gamma
rays) then it is likely that a substance with a shorter half-life will
be more dangerous than one with a longer half-life. But things can get
more complicated and half-life is not the only consideration. Please
don't think that I know more than a superficial amount about
radioactivity. There's also tritium, which is an isotope of hydrogen,
3H, which was widely used to make paint glow (signs, rifle
sights, sometimes as a tracer in the body). It has a half-life of 12.3
years, although one source I found declared that when used as part of
a biological sample (administered as water) then the "biological
half-life" (a phrase I had not seen before) in humans was about 10
days (this refers not to the decay of the tritium, which takes quite a
while, but to how a normal human body processes water). Tritium is not
good in the body.
14C
Radiocarbon
dating (which I tried to explain and was not too successful) is
one of the most widely used methods of dating human remains and
cultural objects. Please follow the link supplied to read about it a
bit. The basic assumption is that an organic (living) object has a
certain percentage of 14C ("Carbon 14") and this percent is
not replenished which the object is dead. So as the 14C
decreases, a reasonable guess about the age of the object can be
made. 14C is convenient because there's a good amount of
carbon in most organic objects, and because the 14C
half-life is commensurate (appropriate amount) to measure much of
human history.
One source I found said that the half-life of 14C is about 5,730 years. The text asserts that the decay constant for 14C is about –.000121. Are these two numbers consistent? Is there some way to check? Well, suppose 14C follows a Cekt formula. If C=1 and k=–.000121 and t=5,730, then Cekt should be about a half. In fact, we computed this (or rather, calculators did) and the result is .499905, which is quite close to a half. I was happy.
The final exam
I will discuss what I regard as a serious difficulty of many 153
students: knowing how to study. I certainly don't want to deny talent
and intelligence as factors, but knowling how to study is
important. I've probably had extended discussions with about half the
students in this class and have been stunned by widely held attitudes
which I believe actively block success (things like, "I don't open the
book ... I can't work with other students ..."). I've tried to make
suggestions and the suggestions mostly have been ignored. I remark
that, well, your way doesn't seem to work too well, and maybe a
sane person might want to try another way. My suggestions aren't
exciting (indeed, I used the word "boring" in class) but I really
believe that, with high probability, they lead to success.
I read and commented on the contents of .the web page I wrote supporting your study for the final exam.
| Thursday, December 3 | (Lecture #26) |
|---|
Here is where I stopped last time. I want to investigate and contrast the ideas of displacement and distance traveled. This might be interesting to physics people.
A "complicated" integral
Let's "compute"
∫01cos(x17)x16dx. If
we want to apply FTC 1, we need to find an antiderivative. Well, the
integrand is certainly not random. There is a pairing which I hope you
notice after more than 90% of a calculus course. The x17
inside the cosine function, and the x16 multiplying
the outside of the cosine function. Since we are trying to
identify a function whose derivative is
cos(x17)x16, to me a natural guess is something like sin(x17). If
we make that guess, then the derivative of sin(x17) is
cos(x17)(17x16) using the Chain Rule. But we
don't want the multiplicative constant 17, so, just as in a bunch of
examples we've already done, we fix up our initial guess to get
(1/17)sin(x17). And this works, and then, using FTC 1, the
definite integral's value is (1/17)sin(x17)|01=(1/17)sin(1).
I'm actually not too interested in the specific value of the integral, but more in how to make the guessing process work. I want to show you how to do this systematically and easily, reducing the chance of error. Of course, the integrand was set up so we could guess. But the process works often enough that people have make some notation which makes it easier to do. Here is what they would write in this case:
| In x-land | ∫cos(x17)x16dx |
|---|---|
| Guess a u | u=x17 |
| Compute du | du=17x16dx |
| Adjust du to match what's in the integral | (1/17)du=x17dx |
| Go to u-land | ∫cos(x17)x16dx= ∫cos(u)(1/17)du=(1/17)∫cos(u) du |
| Antidifferentiate | (1/17)∫cos(u) du=(1/17)sin(u)+C |
| Return to x-land | (1/17)sin(x17)+C |
Of course, this example is constructed so that things work straightforwardly. A chunk of my job is to show you a range of examples and try to help you learn how to recognize situations where this method of antidifferentiation, called the substitution method, will work. Your job, on the other hand, is to practice a bunch of suitable examples (problems in section 5.6).
Another example
Consider
∫x=0x=1x4/(3+x5)dx. I
"admit" (?) that this is an invented example, intended to display the
substitution method but I also assert that similar computations occur
very often in computations coming from "real life". If we want to use
FTC, we need to find an antiderivative of
x4/(3+x5). This is a slightly complicated
function, a rational function (quotient of polynomials). If we take
u=3+x5, then du=5x4dx. Well, we have
x4dx in the original integral, so (1/5)du=x4dx
and the indefinite integral ∫x4/(3+x5)dx in
x-land becomes ∫(1/u)(1/5)du in u-land. This is (1/5)∫(1/u)du
because constant multipliers can be moved outside the integral sign (a
reflection of the derivative of Cf is Cf´). But I can
antidifferentiate this. It is (1/5)ln(u)+C. Now back to x-land and get
(1/5)ln(3+x5). To finish the computation, remember |01. The result is
(1/5)ln(4)–(1/5)ln(3). I would probably leave the answer this way (if
I work with it I may make mistakes). Please note that a naive observer
when asked for the area under y=x4/(3+x5) and
above the x-axis and between y=0 and y=1 would not necessarily expect
an expression involving logarithms. The result is, from that point of
view, weird, wonderful, unexpected ...
QotD
Find
∫x=0x=sqrt(2)x e(–3x2)dx.
The answer involves ...
6 6 6
Less fearsomely, try u=–3x2. The
desired answer can be written as (1/6)–e–6/6.
∫01sqrt(5x+4)dx
I always try to substitute for the center of the difficulty first
(this does not always work, but it helps in lots of examples). In
this example I would try u=5x+4. So then du=5dx so (1/5)du=dx, and, as
an antiderivative (let me leave out the limits right now):
∫sqrt(5x+4)dx=∫sqrt(u)(1/5)du=∫(1/5)u1/2du=(1/5)(2/3)u3/2+C=(2/15)u3/2+C
=(2/15)(5x+4)3/2+C
The outline of this computation is: from x-land to u-land,
antidifferentiate, back to x-land. Now if we really want to compute
the definite integral, look:
(2/15)(5x+4)3/2|01=(2/15)(93/2)–(2/15)(43/2)
Please notice that the x=0 limit does contribute to this
answer -- you can't just ignore it because, golly, x=0. This antiderivative
has a non-zero value at x=0.
My silicon pal does a great job on this (it even cleans up the fractions and powers!):
> int(sqrt(5*x+4),x=0..1);
38
--
15
∫x·sqrt(5x+4)dx
As I remarked in class, I think that most people could have made a
good guess at the previous antiderivative. I can't do this one without
a substitution and some subsequent manipulation. So again let us try
the center of the difficulty, u=5x+4, so du=5dx and (1/5)du=dx. But
now to get to u-land we need to know how to translate x. Since u=5x+4,
we know that u–4=5x and (1/5)(u–4)=x. Therefore:
∫x·sqrt(5x+4)dx=∫(1/5)(u–4)u1/2(1/5)du [to u-land]
(1/25)∫(u–1)u1/2du=(1/25)∫u3/2–u1/2du
[pull out constant multiplier, distribute u powers]
(1/25)((2/5)u5/2–(2/3)u3/2)+C=(1/25)((2/5)(5x+4)5/2–(2/3)(5x+4)3/2)+C [antidifferentiate, and back to x-land. Notice that
1/(5/2)=2/5. etc.].
Although it may be possible to check an antiderivative by
differentiating, you may not want to!
|
∫x2sqrt(5x+4)dx Here I pushed up a power of the x. If you use u=5x+4 again (the center of the difficulty) then as before, (1/5)du=dx and (1/5)(u–4)=x. So the integral becomes: ∫x2sqrt(5x+4)dx=∫[(1/5)(u–4)2sqrt(u)(1/5)du This is not so pleasant but we can do it. Now [(1/5)(u–4)2=(1/25)(u2–8u+16) and so: ∫[(1/5)(u–4)2sqrt(u)(1/5)du=(1/125)∫u5/2–8u3/2+16u1/2du So what did I do there? Well, I squared 1/5 to get 1/25, and then multiplied by another 1/5 to get 1/125. Multiplicative constants can be pulled "out" of the indefinite integral. Other kinds of constants can't! Then I distributed the sqrt(u)=u1/2 over the other terms. Powers of u can be antidifferentiated easily, so we get: (1/125)((2/7)u7/2–(16/5)u5/2+(32/3)u3/2)+C Now back to x-land: (1/125)((2/7)(5x+4)7/2–(16/5)(5x+4)5/2+(32/3)(5x+4)3/2)+C I surely would not want to check this by differentiating! My "pal", in about two-hundredths of a second (.02 seconds) gives this: > int(x^2*sqrt(5*x+4),x);
3/2 2
2 (5 x + 4) (128 - 240 x + 375 x )
-------------------------------------
13125
I hope (I guess!) this is what we have. It sort of looks the same!
|
∫x·sqrt(5x2+4)dx
Here u=5x2+4 (the most "horrible" thing in the integral),
du=10x dx, (1/10)du=x dx (because notice that there is an x
inside the integral -- not an accident!). From x-land to u-land, then,
we get:
∫x·sqrt(5x2+4)dx=∫sqrt(u)(1/10)du=∫(1/10)u1/2du=(1/10)(2/3)u3/2+C
The x did not just disappear! It was needed in this case to be
part of du. And finally we change (1/10)(2/3)u3/2+C to
(1/10)(2/3)(5x2+4)3/2+C. You can check
this by differentiating, if you use the Chain Rule correctly. The 2/3
cancels the 3/2 coming from the power outside, and the 1/10 cancels
the 10 in the 10x coming from what is inside.
|
∫exsin(5ex+7)dx Pattern: the worst thing is certainly inside sine. So I will try u=5ex. Then du=5exdx, and (1/5)du=exdx. From x-land to u-land, to antidifferentiate, and back to x-land; ∫exsin(5ex+7)dx=(1/5)∫sin(u)du=(1/5)(–cos(u))+C=(1/5)(–cos(5ex+7))+C.
Three ln integrals
|
A differential equation and initial condition again
I'm following the text here. We are next supposed to consider a new
sort of differential equation. We have studied such problems as
these:
y´=3x4+{2/x4} and
y(1)=2.
This is an initial value problem, with a differential equation and an
initial condition. We find what's called the general solution by
computing an antiderivative:
∫3x4+{2/x4} dx=∫3x4+2x–4dx=(3/5)x5–(2/3)x–3+C
The perhaps interesting aspects of what was just computed are these: I
first changed {2/x3} to 2x–3, which is a more
standard way to write powers of x. I regard things like sqrt(x) (just
x1/2) and 1/sqrt(x) (surely x–1/2) as
invitations to error, directed personally at me. Unfortunately I
accept these invitations sometimes. Then I antidifferentiated. Making
sure that a minus sign appears in the answer (a consequence of the
transition from –3 to –2) is also something I foul up sometimes. Oh
well. Now onward.
The initial condition y(1)=2 allows us to pick out a particular
solution by finding a value of C in the general solution:
Since y(1)=2, (3/5)15–(2/3)1–3+C=2. This means
(3/5)–(2/3)+C=2 or C=61/15.
The solution is f(x)=(3/5)x5–(2/3)x–3+(61/15).
A different kind of differential equation
We look at dy/dt=ky where k is a constant. The independent variable is
usually called t here instead of x. The reason for t (time)
will become apparent, I hope. Notice that this is a very different
kind of equation, because what's on the right-hand side is a constant
multiplied by y. We can't solve it by just antidifferentiating ky
because we don't know y. So a different approach must be
used. There will be more about such equations in Math 152. This is a
simple example designed to help you work with a number of useful
applications.
Translation into English; what is this?
I asked people about an English language translation of the equation
dy/dt=ky. This is difficult. Here is a possible candidate for such a
translation:
The rate of change of y over time (dy/dt) is directly proportional to y itself. ("Directly proportional" means that when the amount of y changes, that the rate of change of y is changed by k mutliplied by the change.)There are many real phenomena which satisfy this sort of growth (or decay) rule. Examples include:
This is a terrible "translation". I am sorry. Maybe I'd better stick with adding fractions. English is too difficult!
I'll try to discuss solutions and uses of this equation next time.
| Tuesday, December 1 | (Lecture #25) |
|---|
FTC 1
If F´=f, then ∫abf(x) dx=F(x)|ab=F(b)–F(a).
Simple examples
I wrote two "rules" for computations on our exams. They
were:
|
FTC 2
If F(x)=∫axf(t) dt, then F´(x)=f(x).
An alphabet lesson
What is ∫01x2dx? In the last lecture,
we saw with several different techniques that this is 1/3. Then let's
play a little logical game.
Simple example
Describe a function whose derivative is cos(x+ex).
This is either very very easy, or, for reasons that will be discussed
more in Math 152, very very hard. I will give the very very easy
answer here.
One function is F(x)=∫–3xcos(t+et) dt. This is a function whose derivative is cos(sqrt(x)+ex) by using FTC 2.
Another function is G(x)=∫5xcos(w+ew) dw.
Let me compare the two answers. One has inside variable t and the other has inside variable w. This doesn't matter. They both are "satisfactory" answers to the question asked because FTC 2 implies that the derivative of a definite integral with a variable upper parameter is the integrand's value at that upper parameter (hey, I'm using all of the high-priced words!) One answer is a definite integral from –3 to x and the other is a definite integral from 5 to x. Using property (*) from last time, the two answers are different by this: ∫–35cos(s+es) ds. What is this? It is a constant (I'm just using another variable, s, to again bring up the idea of a "dummy variable"). Two functions which differ by a constant have the same derivative. So that's o.k.
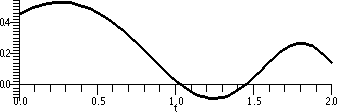 By the way, it can be proved that no one can do much better in
this problem than write the answer as a definite integral. There isn't
any much simpler answer. Software can then plot this function, because
people have spent a great deal of time and effort learning how to
compute good numerical approximations to definite integrals very
rapidly. The picture of F(x), the antiderivative of
cos(x+ex) which is defined above, on the interval [0,2] was
produced by Maple in less than
three-tenths of a second. I am sure other software would do the job as
well.
By the way, it can be proved that no one can do much better in
this problem than write the answer as a definite integral. There isn't
any much simpler answer. Software can then plot this function, because
people have spent a great deal of time and effort learning how to
compute good numerical approximations to definite integrals very
rapidly. The picture of F(x), the antiderivative of
cos(x+ex) which is defined above, on the interval [0,2] was
produced by Maple in less than
three-tenths of a second. I am sure other software would do the job as
well.
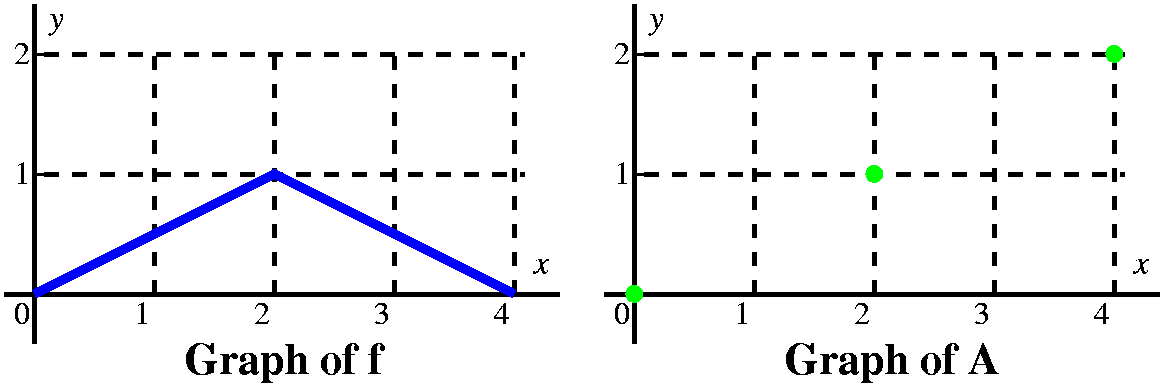
More examples (a textbook problem)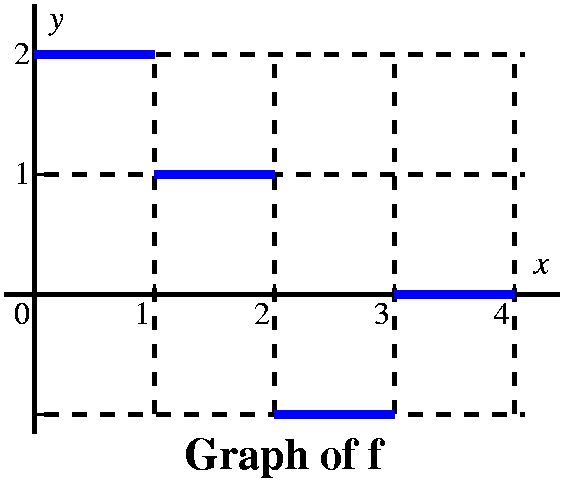 This is problem 23 in section 5.4. The graph of f is given to the
right. The problem asks us to sketch a graph of
A(x)=∫0xf(t) dt. I presume, since f's
graph is given on the interval [0,4], that we are supposed to sketch a
graph of A(x) on the same interval.
This is problem 23 in section 5.4. The graph of f is given to the
right. The problem asks us to sketch a graph of
A(x)=∫0xf(t) dt. I presume, since f's
graph is given on the interval [0,4], that we are supposed to sketch a
graph of A(x) on the same interval.
There are various strategies for analyzing this sort of problem. Since the information is furnished graphically, I'd probably try to do the problem graphically, or at least begin it that way. I would think of the limits, 0 and x, and try to see how the definite integral (which I'd think of as signed area) varied as x varied. |
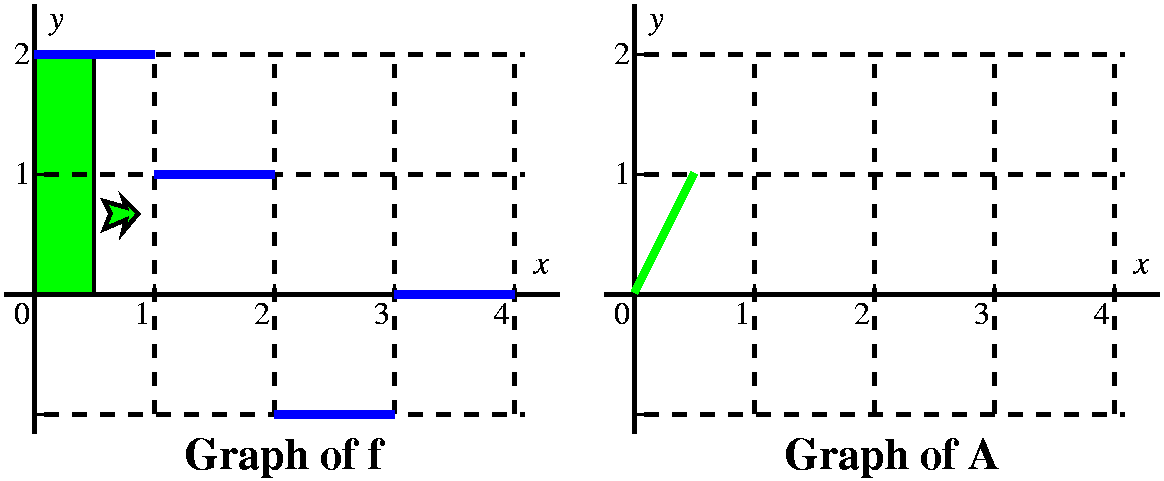 Let's consider first x's between 0 and 1. Here I think
of a vertical line somewhere over the [0,1] interval, moving to the
right. The area between that line and the y-axis, under y=2, is
∫0xf(t) dt. Since the line has height 2,
the area is 2x, and the graph of A is a straight line segment starting
from (0,0) with slope 2.
Let's consider first x's between 0 and 1. Here I think
of a vertical line somewhere over the [0,1] interval, moving to the
right. The area between that line and the y-axis, under y=2, is
∫0xf(t) dt. Since the line has height 2,
the area is 2x, and the graph of A is a straight line segment starting
from (0,0) with slope 2.
|
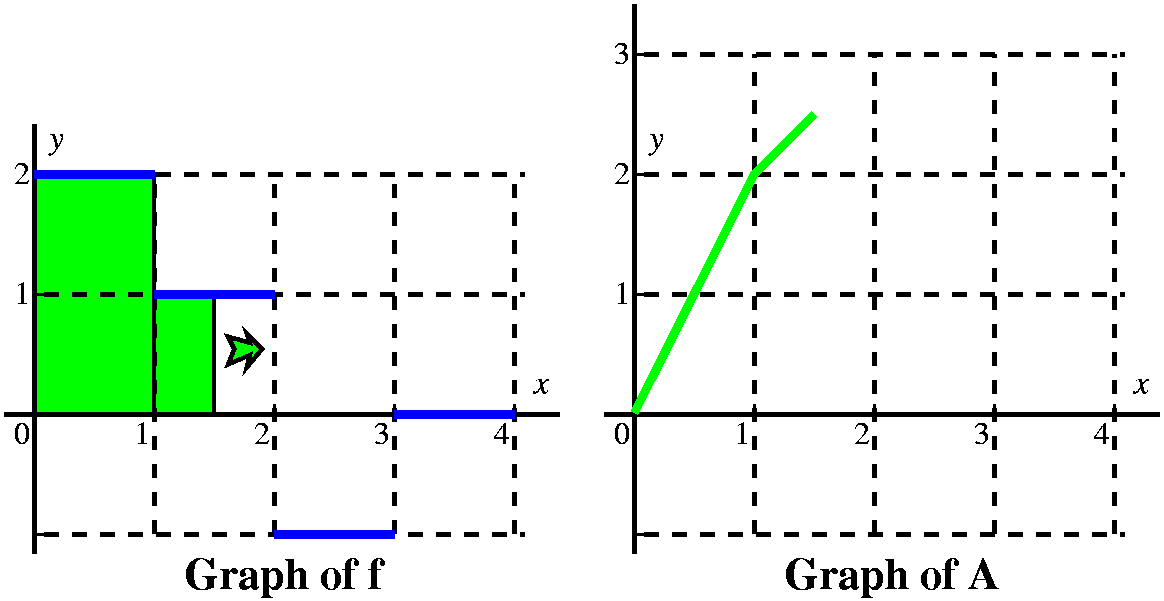 When the vertical line passes x=1, we have accumulated 2 units of
area, and A(1)=2. But now the "profile curve", f, changes height. It
has height 1. We must add to the 2 units of accumulated area the new
area we are getting between x and 1. Since the height of f is 1, and
the base is x–1, we add on 1(x–1) units of area.
When the vertical line passes x=1, we have accumulated 2 units of
area, and A(1)=2. But now the "profile curve", f, changes height. It
has height 1. We must add to the 2 units of accumulated area the new
area we are getting between x and 1. Since the height of f is 1, and
the base is x–1, we add on 1(x–1) units of area.
The graph of A in this interval will be linear with a slope of 1, and it will start from (2,2). |
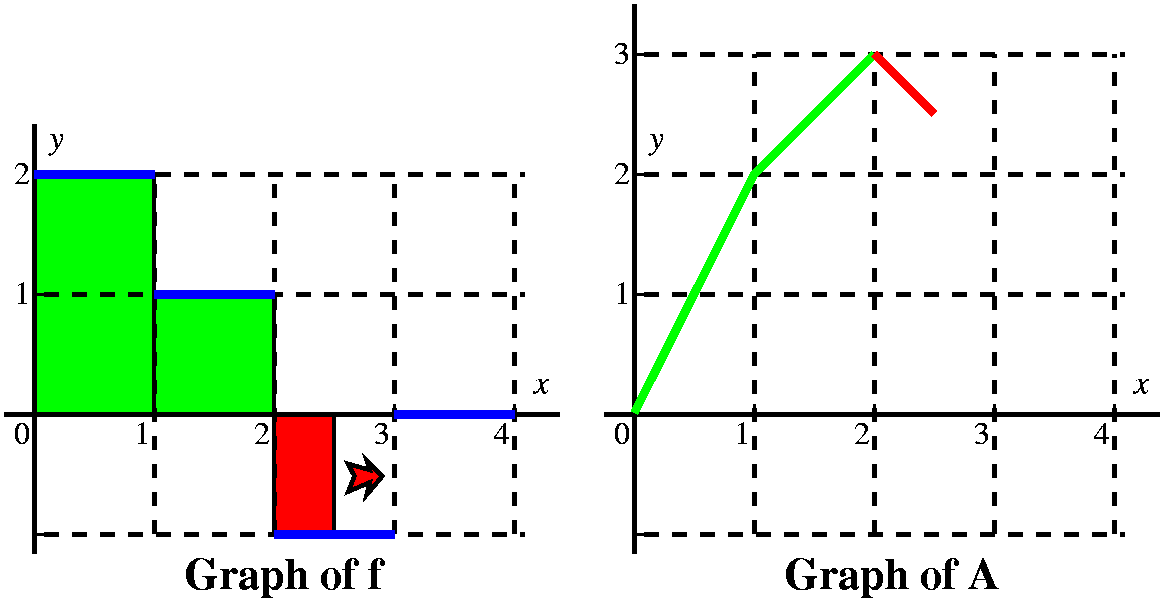 At x=2, we have accumulated 3 units of area, 2 over the interval
[0,1], and 1 more over the interval [1,2]. Now x moves to the right in
the interval [2,3]. The height of f is –1, so the definite
integral will decrease: the geometric area is below the
x-axis. We know A(2)=3 becuase of the accumulated area.
At x=2, we have accumulated 3 units of area, 2 over the interval
[0,1], and 1 more over the interval [1,2]. Now x moves to the right in
the interval [2,3]. The height of f is –1, so the definite
integral will decrease: the geometric area is below the
x-axis. We know A(2)=3 becuase of the accumulated area.
But if x is between 2 and 3, the change in A is (–1)(x–2). So we need to show the graph of A decreasing, and it will be decreasing linearly in x, with a slope of –1. |
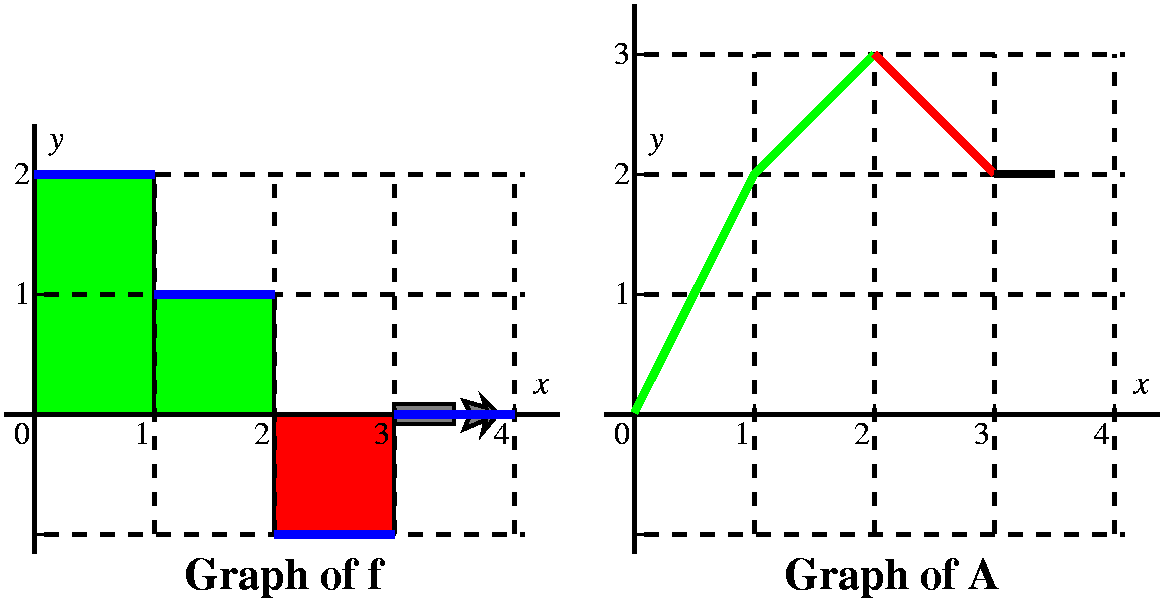 By the time the vertical line has gotten to x=3, it has accumulated
3–1 units of area. Yes, I know that 3–1=2, so actually A(3)=2,
but somehow writing and thinking 3–1 helps me recall that + is assigned to areas above the x-axis and
– is assigned to areas below the x-axis.
By the time the vertical line has gotten to x=3, it has accumulated
3–1 units of area. Yes, I know that 3–1=2, so actually A(3)=2,
but somehow writing and thinking 3–1 helps me recall that + is assigned to areas above the x-axis and
– is assigned to areas below the x-axis.
Between 3 and 4, the height of f is 0 (zero: nothing). There is therefore no change in the area as we move the upper limit on the definite intergral to the right. And therefore there is no change in A, and the graph of A is a horizontal line segment beginning at (3,2). |
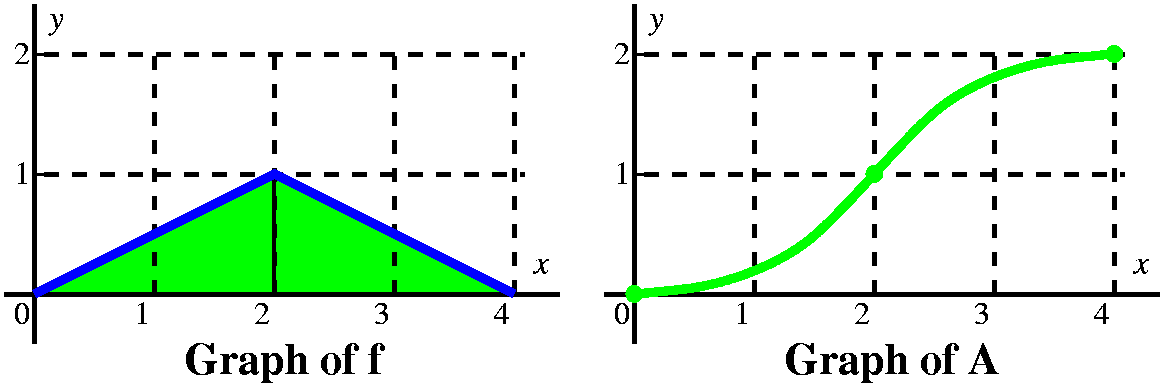
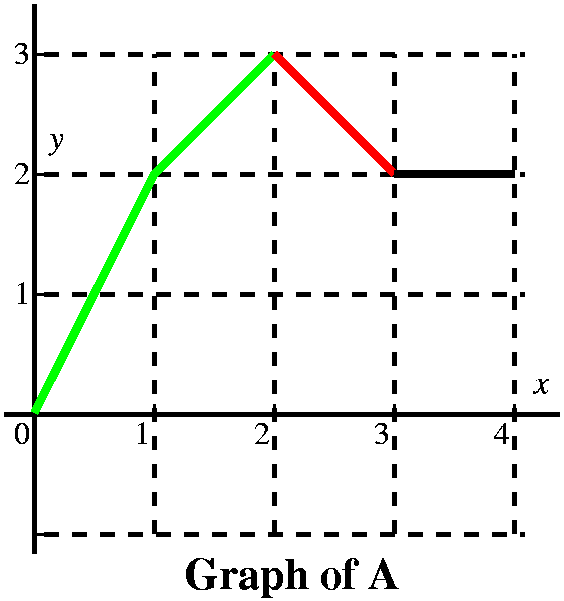 From this we get a very good idea of the graph of A(x). It is 4 line
segments with slopes of 2, 1, –1, and 0. It is a continuous function.
The slopes of A correspond to the heights of f, and actually A is an
antiderivative of f (the antiderivative with the initial condition
A(0)=0), so f is the derivative of A. I think the graph looks like
what's shown to the right.
From this we get a very good idea of the graph of A(x). It is 4 line
segments with slopes of 2, 1, –1, and 0. It is a continuous function.
The slopes of A correspond to the heights of f, and actually A is an
antiderivative of f (the antiderivative with the initial condition
A(0)=0), so f is the derivative of A. I think the graph looks like
what's shown to the right.
|
Part B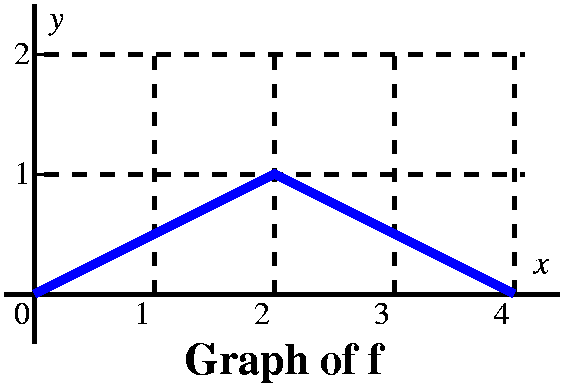 Well, there's actually a part B) to this problem. The graph to the
right is given, and, again, we are asked to graph
A(x)=∫0xf(t) dt. Here the graph is a bit
more complicated (well, it is more complicated to me: the other
function had exactly 4 values, and this function has lots and lots of
values!).
Well, there's actually a part B) to this problem. The graph to the
right is given, and, again, we are asked to graph
A(x)=∫0xf(t) dt. Here the graph is a bit
more complicated (well, it is more complicated to me: the other
function had exactly 4 values, and this function has lots and lots of
values!).
I'll use a strategy different from what we did in A) to understand and solve this problem. |
 Probably I would look at the graph and learn that A(0)=0 (there is
no area from 0 to 0!). I would look a bit more and find that
A(2)=1, because ∫02f(t) dt is the area of
a triangle with base 2 and height 1, and (1/2)(2)(1)=1. Finally, I
would see that A(4)=2, because there are two of those triangles. So I
have the three dots shown to the right on the graph of A.
Probably I would look at the graph and learn that A(0)=0 (there is
no area from 0 to 0!). I would look a bit more and find that
A(2)=1, because ∫02f(t) dt is the area of
a triangle with base 2 and height 1, and (1/2)(2)(1)=1. Finally, I
would see that A(4)=2, because there are two of those triangles. So I
have the three dots shown to the right on the graph of A.
Notice also that the graph of A is increasing because as we move the right limit to the right we are getting more and more area, and this is positive area since it is above the x-axis. |
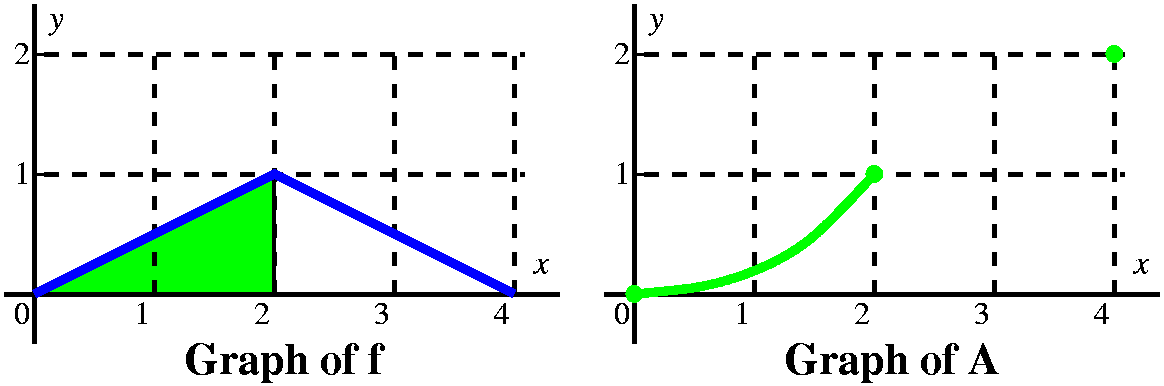 What can we say about the derivative of A in the interval [0,2]? By
FTC 2, this derivative is the function f, and the function f is just
(1/2)x. That means the second derivative of A is 1/2, and this is
positive. So the graph of A between 0 and 2 is concave up, and
connects (0,0) and (2,1).
What can we say about the derivative of A in the interval [0,2]? By
FTC 2, this derivative is the function f, and the function f is just
(1/2)x. That means the second derivative of A is 1/2, and this is
positive. So the graph of A between 0 and 2 is concave up, and
connects (0,0) and (2,1).
I actually know a formula for A, since A(0)=0 and A´(x)=(1/2)x. It must be (I antidifferentiate and get the correct constant!) A(x)=(1/4)x2. So what I see between 0 and 2 is a piece of a parabola. |
 Between 2 and 4, the function keeps increasing. But the slope of the
function, A´, is positive: it seems to be a line segment from
(2,1) to (4,0). But the derivative of that is –1/2, so the
second derivative of A is negative. A is increasing and concave
down. I think the graph is must look like what is displayed to the
right.
Between 2 and 4, the function keeps increasing. But the slope of the
function, A´, is positive: it seems to be a line segment from
(2,1) to (4,0). But the derivative of that is –1/2, so the
second derivative of A is negative. A is increasing and concave
down. I think the graph is must look like what is displayed to the
right.
In fact, between 2 and 4, A´(x)=–(1/2)x+2. I also know that I have accumulated 1 unit of area by the time we get to 2, so that A(2)=1. I can solve this initial value problem: antidifferentiate to get A(x)=–(1/4)x2+2x+C. Use A(2)=1 to get C: –(1/4)22+2(2)+C=1, so C=–2, and the formula for A(x) in this interval is –(1/4)x2+2x–2. We can check this by plugging in x=4, so the result is –(1/4)42+2(4)–2=–4+2(4)–2=2 which is correct. Another thing which is not obvious is that the function A is differentiable. Since A is defined by two nice formulas, it isn't very surprising that A´ exists inside the two halves of the domain. In fact, A is differentiable at x=2, also. This can be checked with effort by looking at the difference quotient (there is a similar check in the workshop problem solution inserted in the Rutgers edition of the textbook). But I am willing to believe that A´(2) exists, because:
|
Movement of a particle
Let's assume that the velocity of a particle traveling on the x-axis
is given as a function of time: v(t)=4t2–t4 for
t between 0 and 5. (As far as I know, this is a rather non-physical
example, but I hope that the questions and ideas contributing to the
solutions are correct and useful.)
| Tuesday, November 24 | (Lecture #24) |
|---|
Last time we saw that if we had a function f defined on an interval [a,b], then we could introduce a rather elaborate collection of objects which are used to analyze f's behavior on all of [a,b].
If [a,b] has a partition P (which break up [a,b]
into a number of subintervals) and a collection of sample
points (the text's intermediate points) C, then we defined
the Riemann sum of f using P and C:
R(f,P,C)=∑j=1nf(cj)Δxj.
If the length of the longest subinterval→0, then (for the
functions we will consider in this course!) the Riemann sums approach
a limit which is called the definite integral of f from a to b
and written ∫abf(x)dx.
Definite integrals have some very useful properties which people use frequently.
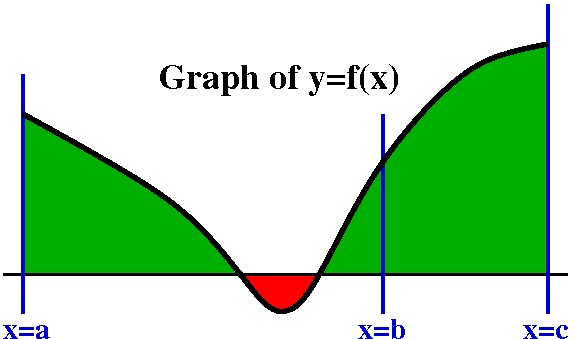 Property (*) and consequences
Property (*) and consequences
Suppose a<b<c. Then
∫abf(x)dx+∫bcf(x)dx=∫acf(x)dx
and I will call this statement (*). I am happy if you believe this
statement. I hope that the picture to the right is enough
verification. The picture has red for area below the horizontal axis
and green for area above the axis because I wanted to remind you how
area is counted for the definite integral. It is possible to prove
this statement from the definition with Riemann sums.
Unexpected consequences of (*)
While most people are willing to believe (*), there are some results
which may take you some time to learn to use. For example, in the
equation
∫abf(x)dx+∫bcf(x)dx=∫acf(x)dx
what if we change b to a? Then we seem to get
∫aaf(x)dx+∫acf(x)dx=∫acf(x)dx
and the only way this could be true is if
∫aaf(x)dx=0.
Most people find this easy enough to believe: this quantity is the
area of a "region" with width equal to zero, and some height, and such
an area should be 0. So any definite integral whose upper and lower
limits are the same must be 0.
O.k., if you believe that one, then I will make another change in the
equation:
∫abf(x)dx+∫bcf(x)dx=∫acf(x)dx.
Change c to a in this equation, and use the fact that the
right-hand side will become ∫aaf(x)dx which we already "know" is
0. So we get:
∫abf(x)dx+∫baf(x)dx=0
and this certainly means that ∫baf(x)dx=–∫abf(x)dx
so that when the limits of a definite integral are interchanged, then
the sign of the integral is changed! (What we are in fact computed is
called an oriented area, and more complicated than what I've told you
so far.)
Example(s) |
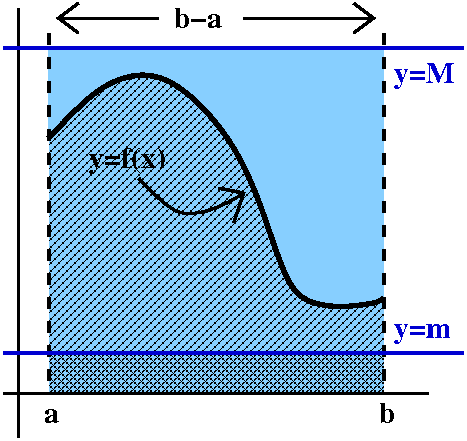 Property (**)
Property (**)This is extremely useful when you are confused and need to make some sort of estimate. Suppose, somehow, you know that all of the values of f(x) on the interval [a,b] are between m and M. That is, you know m≤f(x)≤M for all of those x's. Then (look at the graph!) the "area" (actually the definite integral) will be trapped inside a box. So the result is: m(b–a)≤∫abf(x)dx≤M(b–a). This is because the wiggly region contains the smaller box and is contained by the larger box. It looks silly, but the estimates can really be useful in checking computations. |
I mentioned that definite integrals are used to compute many quantities of interest to engineers, includiong such things as work, power, energy, pressure, volume, length, etc. This may not be too clear right now, but a number of these are discussed in the next course (Math 152). The key is that for all of these quantities, (*) and (**) are true in some way.
Yet another example ...
Here is a final example of how to compute an area (or a definite
integral) in the most direct fashion: by getting the area of a
collection of approximating rectangles, and then analyzing what
happens as the partition gets "finer".
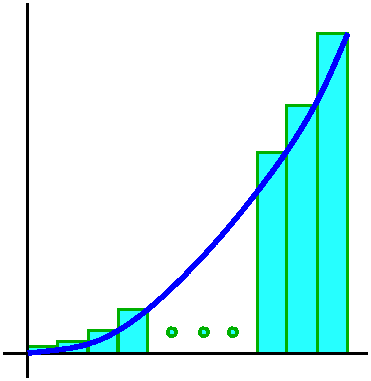
The example is the area under y=x2 from 0 to 1. This means the area enclosed by the x-axis, y=1, and y=x2. It is an area in the first quadrant. We will approximate the area, which is the definite integral ∫01x2dx by a collection of Riemann sums. Here f(x)=x2.
N=5
If we had N=5, the approximation would be
(1/53)(1+4+9+16+25) which is (1/125)(55). The mysterious
part is the 55, of course.
A magic formula
Well, everyone knows (it is in the book on page 317, so ... it is possible to know
it!) that ∑j=1Nj2 is
(1/3)N3+(1/2)N2+(1/6)N.
We actually checked that if N=5 is plugged into this formula, the
result is 55. That's nice. So maybe the formula is correct.
Getting the exact value of the definite integral
Since we know that ∑j=1Nj2 is
(1/3)N3+(1/2)N2+(1/6)N and that the Riemann sum
is this divided by N3, then the value of the Riemann
sum is (1/N3)((1/3)N3+(1/2)N2+(1/6)N)
which is (1/3)+(1/2N)+(1/6N2) and certainly as N→∞, this must approach 1/3. So ∫01x2dx=1/3.
Change the problem: make it harder!!!
These techniques seem to be (they are!) very intricate. Let me show
you how to solve this problem by first making it more
difficult. The people who discovered that the (seemingly) more
difficult problem can be solved very neatly really had a lot of
intellectual courage.
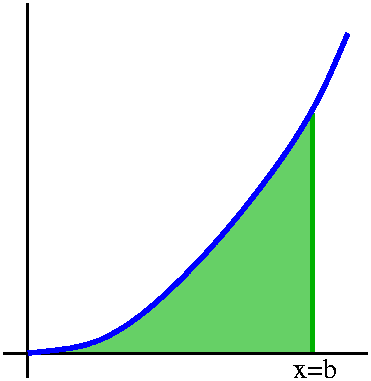 So instead of studying ∫01x2dx, we will study the
function
So instead of studying ∫01x2dx, we will study the
function
A(b)=∫0bx2dx.
We really want to know A(1), but we'll consider this more general
problem anyway.
What do we know?
Well, there is one value of the function that is extremely easy
to compute: A(0)=∫00x2dx=0.
That seems to be the only simple thing. But this is a CALCULUS course, and maybe we should try to differentiate A(b). This, which certainly should seem almost ludicrous, turns out to be the successful approach.
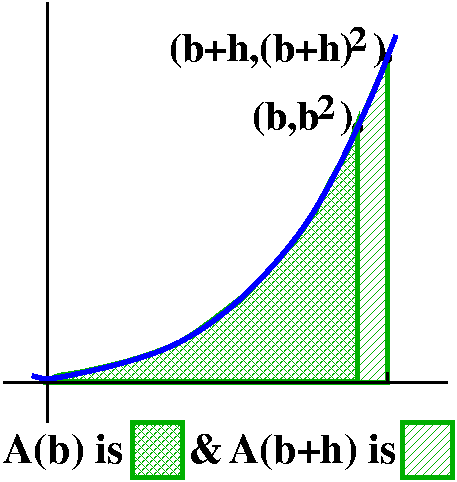 In order to find A´(b) we will need to consider A(b+h)–A(b) and
then divide the result by h.
In order to find A´(b) we will need to consider A(b+h)–A(b) and
then divide the result by h.
Certainly (*) implies that
∫0bx2dx+∫bb+hx2dx=∫0b+hx2dx
so that A(b+h)–A(b) is ∫bb+hx2dx.
But we can use (**) now. f(x)=x2 is increasing on [b,b+h],
so for all x in the interval,
b2≤f(x)≤(b+h)2. So, with m=b2
and M=(b+h)2, we see that
b2·h≤A(b+h)–A(b)≤(b+h)2·h
since h is the width of the interval. Now divide by h:
b2≤[A(b+h)–A(b)]/h≤(b+h)2.
Notice that both estimates →b2 as h→0. This means
that A(b) is differentiable, and that A´(b)=b2.
An initial value problem
We have a function, A(b), with the following properties:
A(0)=0 (initial condition);
A´(b)=b2 (differential equation).
This is an initial value problem. All antiderivatives of
b2 have the formula (1/3)b3+C. If
A(b)=(1/3)b3+C then A(0) must be C, but the initial
condition states that A(0)=0, so C=0. Therefore,
A(b)=(1/3)b3.
Now solve the original problem
Since A(b)=(1/3)b3, then A(1)=(1/3). No problem!
Hey, things are easier than they look
In fact it turns out that we didn't need to figure out the C, because
the value we need to compute the integral from 0 to 1 is A(1)–A(0),
and any antiderivative will give the same result (the "+C" adds and
subtracts, and doesn't change the answer).
The Fundamental Theorem of Calculus, version 1
If F´=f, then ∫abf(x)dx=F(b)–F(a).
In fact, the notation usually used "abbreviates" F(b)–F(a) by
F(x)|x=ax=b. And
"Fundamental Theorem of Calculus" is also usually abbreviated as FTC.
Here is how the original area desired would be computed.
 The area under a bump of sine
The area under a bump of sine
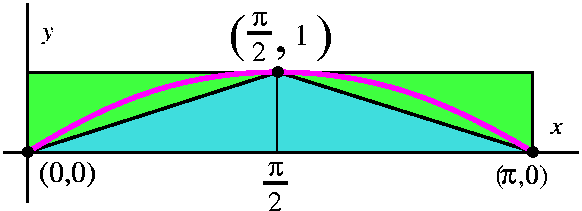
What is the area undo a bump of sine? Well, first think a bit: the
idea of bump maybe means the area between two places where sine is 0
and where the curve is above the x-axis. So the area would be computed
by the definite integral
∫0Pisin(x) dx. Usually having some
estimate of the size of a quantity, even before computing, is a good
idea. Otherwise you may make some simple error, and get some result
which is a huge mistake.
One overestimate of this definite integral is obtained by
looking at a rectangular box which contains the area. The width of the
box is Π and its height is 1, so the integral should be less than
Π·1=Π. An underestimate of the area could be gotten by
looking at two triangles under the graph. Each has base Π/2 and
height 1, so the total area of the two triangles is
2·(1/2)·(Π/2)·1=Π/2 (the 1/2 comes from the
formula for the area of a triangle). One student suggested 0 as an
underestimate. While that is certainly valid, I like under- and
overestimates which are closer to the exact answer (as long as I don't
have to work very hard!). Now we know
Π/2≤∫0Πsin(x) dx≤Π.
To compute this area exactly, we use FTC. We need an antiderivative of
sine, and that happens to be –cos(x). So:
∫0Πsin(x) dx=–cos(x)|0Π=–cos(Π)–(–cos(0))=–(–1)–(–1)=2. The
(potential!) confusion of minus signs occurs often when applying FTC,
so some care is needed. The exact area is 2, and this is certainly
between Π/2 and Π.
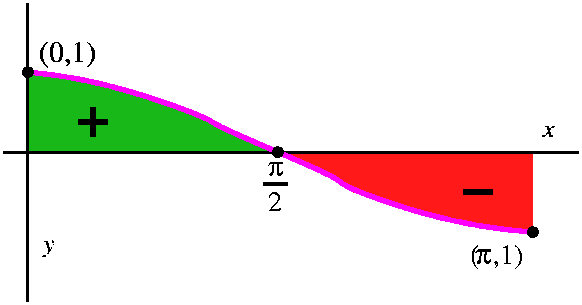 A fake computation: the "area" under a bump of cosine
A fake computation: the "area" under a bump of cosine
I then tried to rush ahead and compute the "area" under a bump of
cosine. Or, rather, I compute this definite integral: ∫0Πcos(x) dx. I asserted that the
result should be ... well, should be ... something.
Here is the computation using FTC, since an antiderivative of cosine
is sine.
∫0Πcos(x) dx=sin(x)|0Π=sin(Π)–(sin(0))=0–0=0.
What happened to the "area" under the bump? We computed a definite
integral, and that's the limit of Riemann sums, and they count
geometric area under the x-axis negatively. The graph of cosine on the
interval [0,Π] exactly balances the positive over-the-axis region
with a negative under-the-axis region. So it is 0 both
computationally and geometrically!
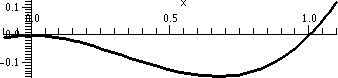 Another bump but negative
Another bump but negative
I asked students what the curve y=x2(x–1) from 0 to 1
looked like. After a while we got a picture similar to what is shown
to the right. I asked what the area was inside the bump. Please
observe that the function is negative, so the definite integral would
be negative, but the area would be positive.
A solution might go like this:
∫01x2(x–1)dx=∫01x3–x2dx=(using FTC)=(1/4)x4=(1/3)x3|01=(1/4)–(1/3)=–1/12.
Therefore the area is 1/12.
Return of the second exam
I returned the second exam. Information about grading and statistics
concerning the results are here. If
you think there's been a mistake made with the grading of your exam
(an almost certain event, considering the number of problems, the size
of the class, and the too fallible human who did the grading), please
check the grading guide, and then bring the exam to me.
I note that the median grade, which I regard as probably the most important number statistically for such happenings, is up from the first exam median.
Course grades will be strongly influenced by both your own efforts and also how the class as a whole does on the Math 151 final. Therefore the final exam results will be used to calibrate or measure or compare performance of the 153 students with the overall 151 group's work, and I will adjust course grades appropriately. I mean that the group achievement will be considered, so it is in the interest of individual members of the class that the whole class do as well as possible!
| Thursday, November 19 | (Lecture #23) |
|---|
| Tuesday, November 17 | (Lecture #22) |
|---|
3 2
(n + 1) (n + 1)
12+22+...+n2 = -------- - -------- + n/6 + 1/6
3 2
which was known in many cultures allows the computation of areas
under y=x2. We could get even more. For the sum of the
first n seventh powers (that is,
17+27+...+n7) the result is
8 7 6 4 2
(n + 1) (n + 1) 7 (n + 1) 7 (n + 1) (n + 1)
-------- - -------- + ---------- - ---------- + --------
8 2 12 24 12
In a number of cultures, this sort of information was treated almost
as a secret, and the details and use were forgotten. Similar, even
more complicated results would allow areas of the trig functions and
even certain exponentials to be computed. But ... there's a better
way. But first I want to convince you that the sort of problem we're
looking at is worth thinking about. Most engineers, once they're out
of calculus courses, never compute an area again. But they do compute
other things. Let me show you an example of an "other thing".
A question of blood... I asked how we could estimate how much blood the heart pumps out to
the body, drawing an especially silly picture on the board (look
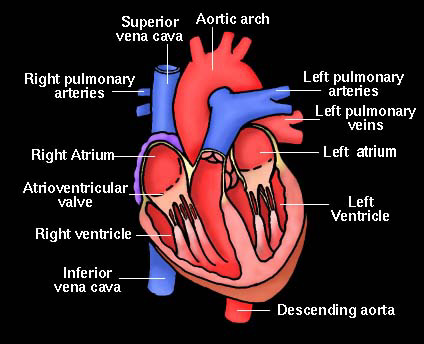
left). Knowing the quantity of (hopefully!) oxygenated blood which is
pushed around the body can be a useful part of health assessment. How
can we measure the blood flow through the aorta, the major artery
emerging from the heart? A better diagram of a heart is to the
left. The heart is a very complicated and wonderful pump.
I asked how we could estimate how much blood the heart pumps out to
the body, drawing an especially silly picture on the board (look
left). Knowing the quantity of (hopefully!) oxygenated blood which is
pushed around the body can be a useful part of health assessment. How
can we measure the blood flow through the aorta, the major artery
emerging from the heart? A better diagram of a heart is to the
left. The heart is a very complicated and wonderful pump.
|
 |
 The Aztec solution
The Aztec solution
One method might be to take a knife, preferably an obsidian knife, and
rapidly cut through the chest wall, sever the aorta, and cause the
blood that would flow through it to fill up a bucket. In about five
minutes we'd probably have a good idea of how much blood flows through
the aorta. There are several criticisms possible of this
"protocol". One criticism might be that, well, maybe the person
involved might not be good for much afterwards. Another criticism
could be that this would not show the actual pumping capacity of the
aorta, because maybe within a minute or two some ... difficulties
would occur. In some sense, this Aztec protocol is the ultimate in
what might be called destructive testing. By the way, obsidian
is "a dark glassy volcanic rock formed from hardened lava" and was
actually used for certain similar purposes in that culture.
Another solution: cardiac catheterization
The American Heart Association and the NIH (National Institutes of
Health) both have lots of information about this. Here are some quotes
from these sources:
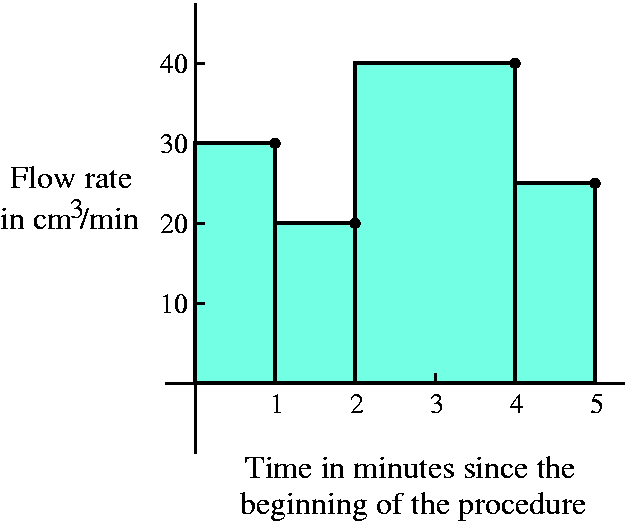
| Elapsed time | Fluid flow rate |
|---|---|
| 1 min | 30 cm3/min |
| 2 min | 20 cm3/min |
| 4 min | 40 cm3/min |
| 5 min | 25 cm3/min |
This isn't much information. But how can we use what we've learned? A standard way to use these numbers is the following. It is certainly very approximate in this case.
At the end of the first minute, we're told that the flow is 30 cm3/min. Hey, we could estimate how much blood is pumped by making the assumption that the flow rate is constant during the time interval involved. Then we see that 30 cm3/min·1 min=30 cm3 (flow rate multiplied by duration) would be pumped. I am not asserting that this is necessarily correct. It is an estimation. We are using the information, and the method is very simple. Similarly, during the second minute, we can estimate that 20 cm3/min·1 min=20 cm3 is pumped. The flow rate changed during the second minute. We're faced with a slightly different "challenge" in using the third line of the table. It has elapsed time (since the start of the procedure) as 4 minutes. So the duration has now changed from 1 minute to 2 minutes. (Why? Well, y'know, in the real world things maybe don't work as you'd like. Maybe the machine broke, or the technician didn't pay attention, or ... in any case, we need to work with the data we have!) So during those two minutes, we have (flow rate·duration) an estimate of 40 cm3/min·2 min=80 cm3 blood pumped. Finally, in the last minute of this procedure, we estimate that 25 cm3/min·1 min=25 cm3.
|
Let me abbreviate just a bit. The units are repetitive and I will omit
them (this is a math course!). So here are the essential details of
the computation: 30·1+20·1+40·2+25·1=155. That's what we're computing. If we wanted a picture of the computation, maybe what is shown to the right gives you some idea. The dots represent the actual known data. The area of the rectangles shown is given by the product of the appropriate flow rate and duration. Yes, there are other possible approximations using the data given. We will study some of them in Math 152, but here only a rather simple-minded approach will be used. |
 |
More information
There is another complication which has occurred, and I hope you notice it. Some of the flow rates (2 min 30 sec and 3 min)are negative. Could this happen? Well, actually maybe yes. The heart is a terrific pump but maybe sometimes things don't always synchronize well or work perfectly: maybe the heart valves don't close all the way or don't close at precisely the correct time in the pumping cycle, etc. This complicates our task. We could ask what the heck we want to measure in this situation, and several answers are possible. We might want to measure the total pumping effort of the heart. Or we might want to know the net amount of oxygenated blood which is pushed out into the body. Let me look at the second quantity. In that case, the negative flow rates affect the total blood pumped because, indeed, that amount in that time should be subtracted, just like the sign of the flow rate indicates, from the total. | ||||||||||||||||||||||
|
What should be computed here? If we do flow rate multiplied by
duration, we should be consistent (the units!) and realize that, for
example, 3 min 30 sec is 3.5 minutes. So the numerical computation
here is 32·.5+30·.5+28·.5+20·.5+(–6)·.5+(–8)·.5+34·.5+34·.5+40·.5+43·.5+25·.5=119. And this estimate, using this data, is 119 cm3. (Ms. O'Sullivan asserts that the total is 109. Hah!) This is much less than the earlier figure, I guess because the data at 4 minutes over a duration of 2 minutes led to a big overestimate.
| ||||||||||||||||||||||
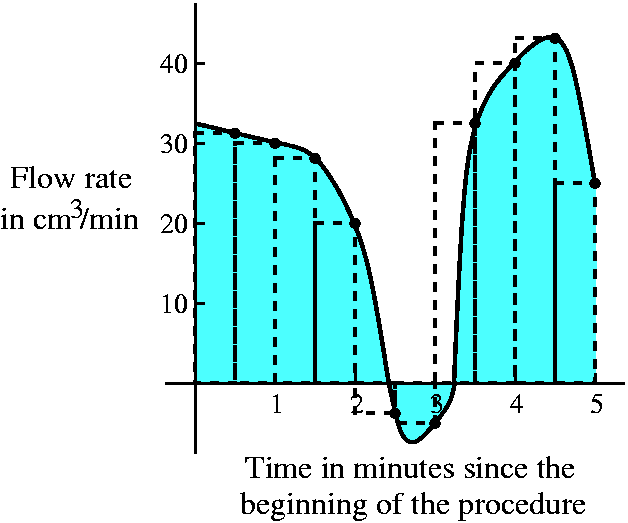
Ideally ... You might imagine that ideally we make lots and lots of measurements (in fact, this is more like what is done, because I think there is a computer recording the flow rates very frequently and then making the computations that I'm discussing in such a silly way). What should we think about? We could have lots and lots and lots of data points. And then the rectangles get very thin. And then the data points look very much like a curve. The number that's wanted is the total blood pumped out to the body, but the picture which might result could look a lot like what is shown here. I have again overlaid it with the rectangles from the previous discussion. So it seems there might be some kind of flow rate curve, and that the blood pumped out to the body, the net blood out, is the area of the colored regions above the curve minus the area of the colored region below the curve. I hope that you can see some resemblance between this and the discussion of the area of the hand which we did previously. Here we are approximating quantities of liquid, and there we were trying to approximate areas. It turns out that this computational idea can be applied in many situations, and it is used in essentially all fields of engineering and applied science. I now need to tell you the official vocabulary. |
Mass from density measurements
 I very briefly mentioned another almost realistic setup. We
might have a bar with varying densities whose total mass we want to
estimate. A sort of picture is to the right, with the different colors
used to imply different densities. Direct measurement (lifting the
bar, for example) might not be feasible. We could imagine taking small
samples of the bar's materail at several points, and then measuring
the densities of these samples. We could then multiply the density by
the appropriate length of the bar and take the sum of these quantities
as an estimate of the bar's mass. This would be a situation whose
mathematical outline would be very similar to the blood flow analysis
we've just done.
I very briefly mentioned another almost realistic setup. We
might have a bar with varying densities whose total mass we want to
estimate. A sort of picture is to the right, with the different colors
used to imply different densities. Direct measurement (lifting the
bar, for example) might not be feasible. We could imagine taking small
samples of the bar's materail at several points, and then measuring
the densities of these samples. We could then multiply the density by
the appropriate length of the bar and take the sum of these quantities
as an estimate of the bar's mass. This would be a situation whose
mathematical outline would be very similar to the blood flow analysis
we've just done.
Vocabulary
Start with the following: a function f defined on an interval [a,b].
|
What this means geometrically ... To the right is my attempt to show you what a Riemann sum might look like. But I've made it quite simple. There are only seven subintervals, and the curve which is the graph of f(x) is also not too complicated. The dots on the x-axis denote the sample or intermediate points, and the vertical lines above them are the lengths f(cj). The boxes have areas which are equal to the pieces of the Riemann sum, f(cj)δxj. The f(cj) is the height and the Δxj is the width of a rectangle. | 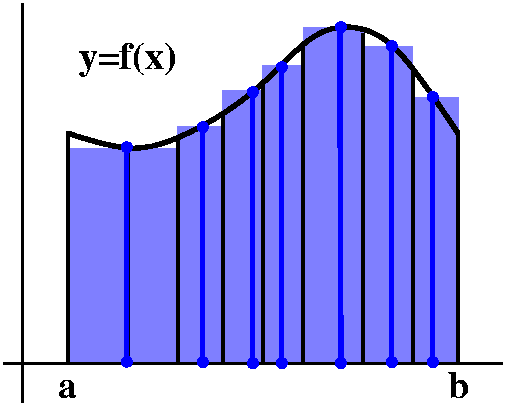
|
|
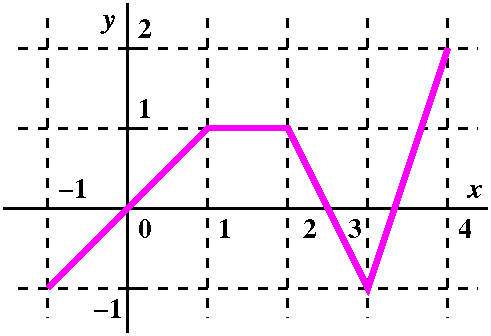
An example To the left is a graph of a function, y=f(x), where f is defined on the interval [0,5]. f's graph is two line segments, the first horizontal from (0,1) to (2,1) and the second tilted from (2,1) to (3,0), followed by the lower half of a circle of radius 1 centered at (4,0), a circular arc going from (3,0) to (4,–1) to (5,0). |
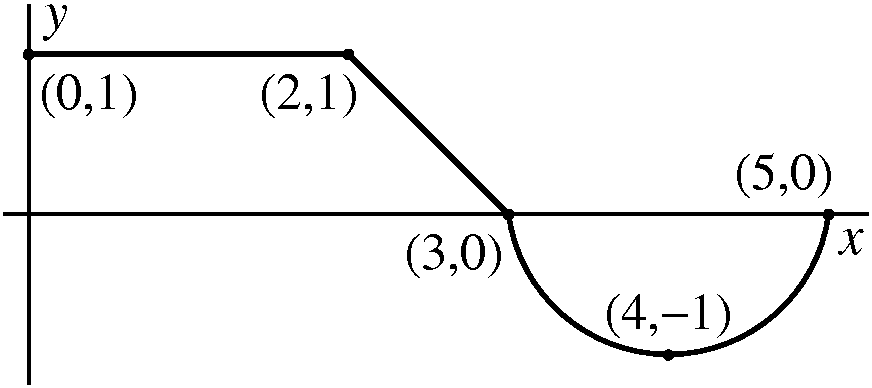
|
| Here are some partitions, choices of sample points, and the resulting Riemann sums. | |
| Partition 0, 2, 3, 5. Sample points 1, 3, 4. The function values at the sample points are: f(1)=1, f(3)=0, f(4)=–1. Riemann sum 1(2–0)+0(3–2)+(–1)(5–3)=0. | 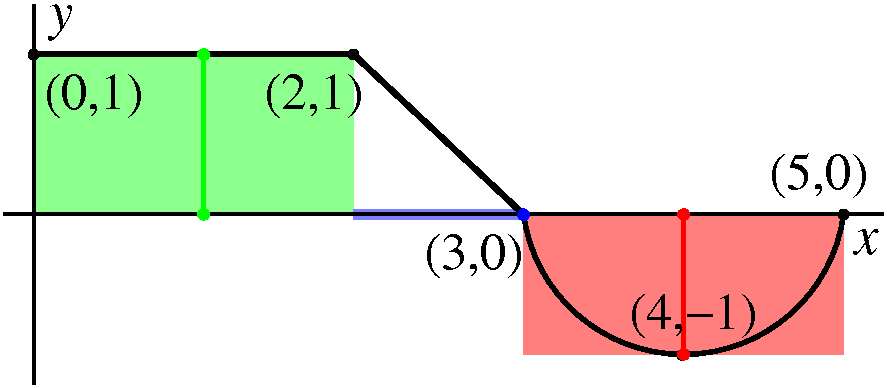 |
|
Choosing the sample point at 3 gives a zero contribution to the Riemann sum. | |
| Partition 0, 2, 3.5, 5. Sample points 1, 3, 4. The function values at the sample points are: f(1)=1, f(3)=.5, f(4)=–1. Riemann sum 1(2–0)+.5(3.5–2)+(–1)(5–3.5)=1.25. | 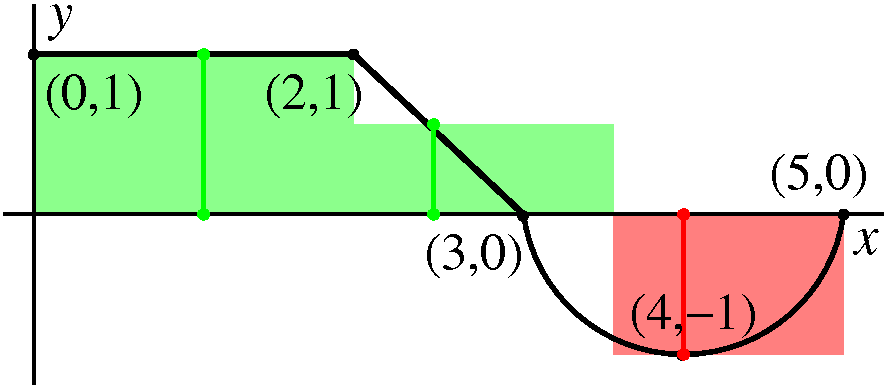 |
|
Partition 0, 2, 3.5, 4.5, 5. Sample points 2, 2, 4, 5. The function values at the sample points are: f(2)=1, f(2)=1, f(4)=–1, f(5)=0. Riemann sum 1(2–0)+1(3.5–2)+(–1)(4.5–3.5)+0(5–4.5)=2.5. | 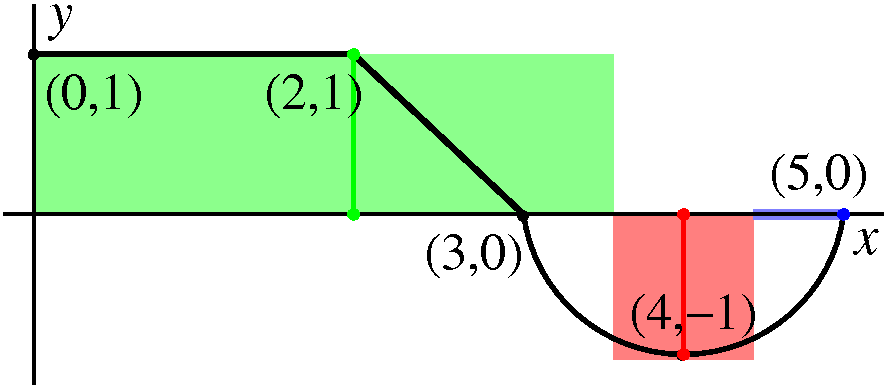 |
|
The definition allows the sample point to be on the boundary of the
subinterval, so two adjoining subintervals could possibly share their
sample points. This is a bit wasteful in terms of information,
though. Also notice that the rectangle on the rightmost interval has height 0. | |
| Partition 0, 1, 2, 3, 4, 5. Sample points .7, 1.44, 2.5, 3.5, 4.75. The function values at the sample points are: f(.7)=1, f(1.44)=1, f(2.5)=.5, f(3.5)=–sqrt(3/4)≈–.866, f(4.75)=–sqrt(7/16)≈–.661. (The numbers for f's values at 3.5 and 4.75 come from the equation of the lower unit semicircle, –sqrt(1–x2), suitably translated to the right.) Riemann sum 1(1–0)+1(2–1)+.5(3–2)+(–.866)(4–3)+(–.661)(5–4)=.973. | 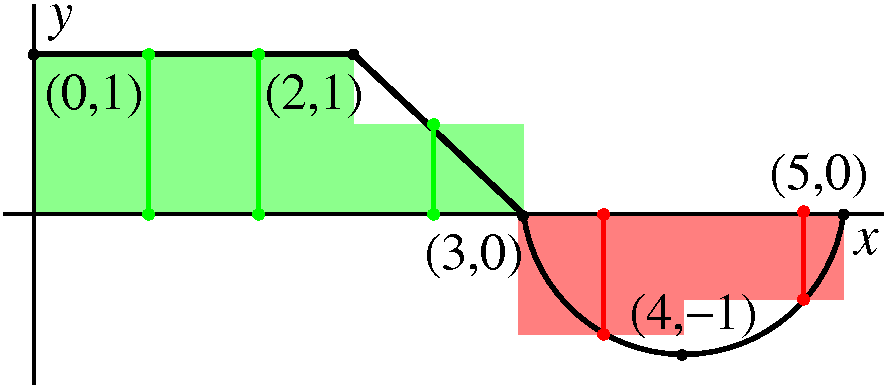 |
|
Notice that putting another sample inside the interval from 0 to 2
didn't improve the approximation very much. If taking samples is
difficult or expensive (and it might be in real life!) then probably
increasing the sampling where functions wiggle a lot rather than where
the values are (relatively) constant is a good idea. This is, in fact,
what the approximation strategies inside most calculators try to do.
Part of the impression I would like to leave with you, even with just a few examples, is that Riemann sums can be quite complicated objects. They can be irritating to compute, and there are so many of them that understanding them may be difficult. | |
| Thursday, November 12 | (Lecture #21) |
|---|
 Hand area
Hand area
What is the area of my hand? There was, of course, some laughter. But
the question and other similar inquiries, while superficially silly,
is actually quite important. Appropriate drug doses are sometimes
calculated in terms of BSA, body surface area. This is
especially important when prescribing drugs for infants or drugs with
strong side-effects (for example, some drugs used in cancer
treatment). And knowledge of body surface area is important in trying
to understand heat balance when people exercise. There are many
formulas for BSA in addition to the Dubois and Dubois formula
which was mentioned in an earlier workshop problem.
So my question is much more modest: how can we compute the area of my hand? We discussed this. There are many methods, but if you think about area, there are really not very many shapes whose area we can compute exactly. The most important and simplest shape is a rectangle, where we know the area is the product of the length and width. We should try to take advantage of this. So look at an image of my hand, and ... well, after discussion we came up with this:
|
I'll suppose first that I put the image of the hand in a square grid
which is, say, 1 mm (millimeter) on a side. I don't know if this is
physically too reasonable, but, what the heck, I could get something
that looks like the picture to the right.
Then I could count the grid boxes which are entirely within the hand image. There was some objection to this, because, you see, I could always be a little clever (?) and maybe sort of count some boxes which are almost entirely in and then compensate by dropping the count by 1 if I count a bunch of those. |
 |
| I commented that I wanted a process (an algorithm) which could be done totally "mechanically", leaving nothing to choice, and which was extremely simple-minded. | |
|
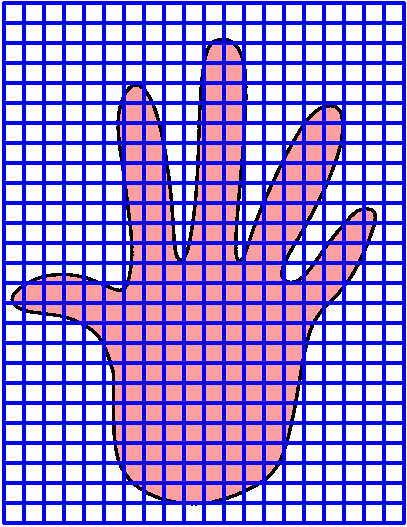
I'll suppose first that I put the image of the hand in a square grid
which is, say, 1 mm (millimeter) on a side. I don't know if this is
physically too reasonable, but, what the heck, I could get something
that looks like the picture to the right. I think if I count correctly there are a total of 18 boxes entirely inside the hand image. | 
|
|
Now for an overestimate. Let me start with the boxes which are
entirely inside, and then add on any boxes that have even the
slightest "tinge" (?) or hint of the hand image inside. Again, maybe
there are objections: we could be cleverer (?) and sort of estimate
how much of a box is inside, etc. But then we would have to make
decisions, and some of those decisions maybe could be difficult. Here,
if we have a simple-minded scheme, I'll bet that any two people will
come up with the same answer. At least we get a result that's stable,
and probably doesn't depend on the observer too much.
There are 18 all-inside boxes, and (if I count correctly!) 60 more boxes are needed to cover all parts of the hand image. The total of the outside boxes is therefore 78. |

|
|
The result? If I believe that area of bigger shapes is bigger, then I see that the area of the hand is between 18 mm2 and 78 mm2. And there is a huge gap between these over- and underestimates of 60 mm2.
More information? | |
|
We get try a grid with more subdivisions: this is called
refining the grid. We could just halve the size of the square
sides. Maybe the result is something like what is shown to the right.
Now the idea is maybe not so easy to implement, at least for human beings whose eyesight and counting ability is not so perfect. But we can try anyway. |
|
|
Well, if I have counted correctly, there are 63 new squares which are completely inside the hand image. This is in addition to the 18 old squares. But, wait: the new squares have sides which are half the length of the old squares. So each of the new squares has one quarter the area of the old squares. So actually we have now succeeding in underestimating the area by 18+(63/4)=25 and 7/8. |  |
| Now let's get an overestimate. We need to add on all of the little squares which contain any part of the hand image. If I have counted correctly (!!) there are 118 of them. That means we need to add one quarter multiplied to 118 to the previous underestimate in order to get the corresponding overestimate. So 118/4 is 29 and a half. Add this on to the previous 25 and 7/8, and the overestimate is 45 and 3/8. |

|
Underestimate, overestimate, and gap
Let me summarize what we have done:
| Underestimate | Overestimate | Gap | |
|---|---|---|---|
| 1-by-1 squares | 18 | 78 | 60 |
| 1/4-by-1/4 squares | 25.875 | 45.375 | 29.5 |
| And so on ... | |||
The secret is that this sort of approach is just about all we can do with real physical quantities. You can really only make better (or worse!) estimates: over- or underestimates. The ideas outlined here, taking finer and finer grids, will lead to overestimates which shrink and underestimates which increase, so that (we hope!) the gap between them →0: refine until you get as close as you want. And this is about all we can do. I don't think the situation is hopeless, but I do think it is compicated.
Attribution
The neat idea of asking for the area of "my hand" is something I
borrowed from Professor J. Rosenstein
of our math department. I think it is clever. It is a question which
brings up important ideas immediately and clearly.
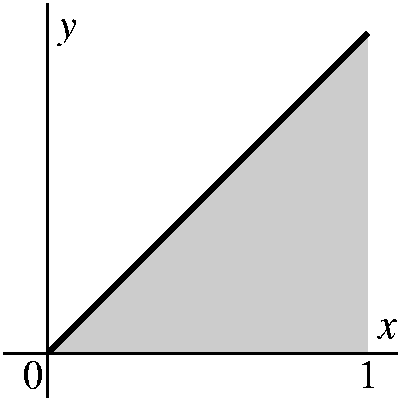 An exact computation
An exact computation
We discussed if we could do an exact computation, not just an
estimate, and this I was happy to try, since many people seemed
rather distressed about the statements made previously. So I will
present a simple example of a general idea. The general idea is very
successful, although the simple example may seem to be
overelaborate. I will try to compute the exact area "under" y=x for
the interval [0,1]. (Yes, I am aware that we know this area --
the ideas are what is important -- as soon as we get the ideas we'll
be able to do much more complicated computations.)
How to begin
We will try to get over- and underestimates of the area We could
divide the interval [0,1] into 4 equal parts using 0 and 1/4 and 2/4
and 3/4 and 1, which I'll choose to call 4/4.
Then put rectangles underneath y=x in each
subinterval. We will be slightly economical and put the largest
rectangles we can under the y=x, but we will be slightly simple-minded
and only look at rectangles which have sides parallel to the
coordinate axes. Then we compute the area of these rectangles:0 1 1 1 2 1 3 1 --- · --- + --- · --- + --- · --- + --- · --- 4 4 4 4 4 4 4 4The 1/4's come from the width of the rectangles, and the varying heights (even including the somewhat absurd 0/4) from the heights of the rectangles. | 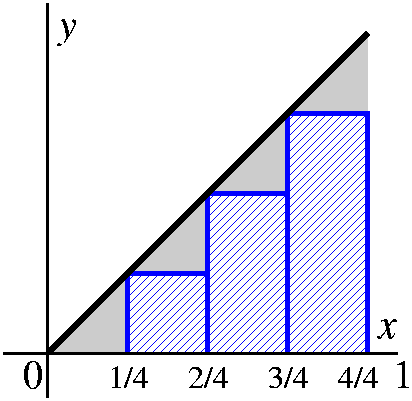
|
Now we need an overestimate, and the true area will
be "captured" between these two estimates. Again, we will use the
interval divided into 4 equal pieces, and rectangles with sides
parallel to the coordinate axes which just contain the region of
interest to us. So the area of these rectanges is:1 1 2 1 3 1 4 1 --- · --- + --- · --- + --- · --- + --- · --- 4 4 4 4 4 4 4 4 | 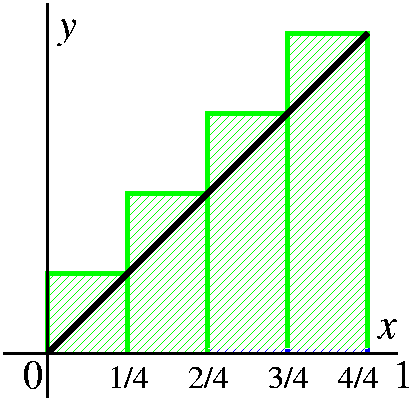 |
| Finally, if we want to see how much gap or error there is between these over- and underestimates, we can look at the area that is inside the big rectangles and outside the small rectangles. The result (because y=x is so simple!) is 4 squares, each with side length 1/4. So the gap is 4(1/4)(1/4)=1/4. | 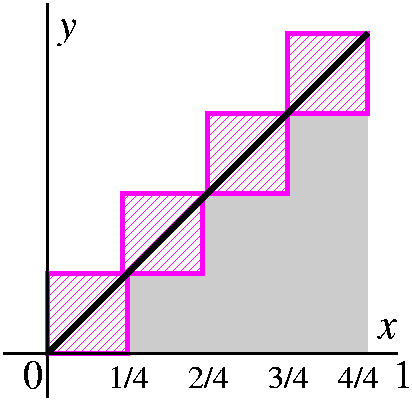 |
The whole setup
We could do something similar with other numbers of
subdivisions of [0,1]. Here are some numerical results:
| # of subdivisions | Underestimate | Overestimate | Gap |
|---|---|---|---|
| 4 | .37500 | .62500 | .25000 |
| 10 | .45000 | .55000 | .10000 |
| 25 | .48000 | .52000 | .04000 |
| 100 | .49500 | .50500 | .01000 |
What really happens, in general
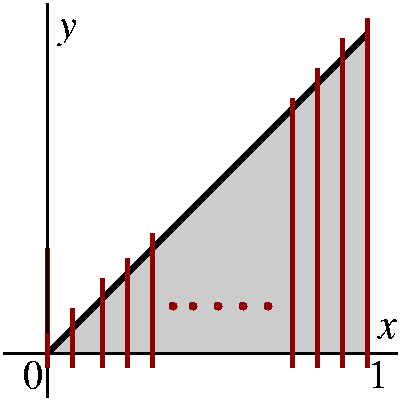 Here it helps to get a little bit abstract. Suppose we divide the
interval [0,1] into n equal pieces, where you should think that n is
some large integer. Then the underestimate will have total area (using
heights over the left-hand endpoint of each subinterval shown in the
diagram to the right)
Here it helps to get a little bit abstract. Suppose we divide the
interval [0,1] into n equal pieces, where you should think that n is
some large integer. Then the underestimate will have total area (using
heights over the left-hand endpoint of each subinterval shown in the
diagram to the right)
0 1 1 1 2 1 3 1 n-1 1 --- · --- + --- · --- + --- · --- + --- · --- + ··· + --- · --- n n n n n n n n n nIn fact, we can "massage" this underestimate a bit and get for the underestimate:
So what happens as n→∞? Since the gap is 1/n, this will →0. So let me look at the overestimate. This is (1+2+3+...+n)·(1/n2). Let's get a formula for 1+2+3+...+n.
A formula
You may remember the trick (maybe done in high school when you studied
arithmetic progressions). The trick is writing two versions of the sum
in oppositite order. Look:
1 + 2 + 3 + 4 + ... + (n-1) + n n + (n-1) + (n-2) + (n-3) + ... + 2 + 1Now add the sums columnwise. So we get 1+n which is n+1 and 2+(n–1) which is n+1 and ... all of the column sums are the same (that's right because the top is going up by 1 each step while the bottom is going down by 1 each step). There are n of the n+1's, so the total of all of the numbers is n(n+1). But this is two copies of the sum we want, so we need to divide by 2.
I think we have verified that 1+2+3+...+(n–1)+n is [n(n+1]/2. And the overestimate of the area, is this divided by n2. So a formula for the overestimate is [n(n+1]/[2n2]. What happens to this as n→∞? Well, we have studied such limits, and we could either divide top and bottom by n2 or we could use L'H twice. In any case, the limit will be 1/2.
A spectacular result?
I have now proved (done an exact computation!) that the area of
the triangle is 1/2. And I guess I knew that. But this whole approach
is a template for more complicated reasoning.
Notation
We will need some notation. Lots of sums occur when we do area
computations, and also many other computations. So a special way of
writing these sums which takes less space has been developed. The
Greek capital letter sigma, ∑, is used. Here are some examples:
| Examples of summation notation | |
|---|---|
| Written out | Abbreviated |
| 1+2+3+4+5 | ∑j=15j |
| 32+42+52+62 | ∑j=36j2 |
| {1/2}+{1/4}+{1/6}+{1/8} | ∑j=14{1/[2j]} |
| 1–2+3–4+5 | ∑j=15(–1)j+1j |
The notation, once you get used to it, is wonderfully economical. I should remark that the summation index, which is j in all of the examples above, doesn't really matter. That is ∑j=13j4 and ∑k=13k4 both mean the same thing, which is 14+24+34.
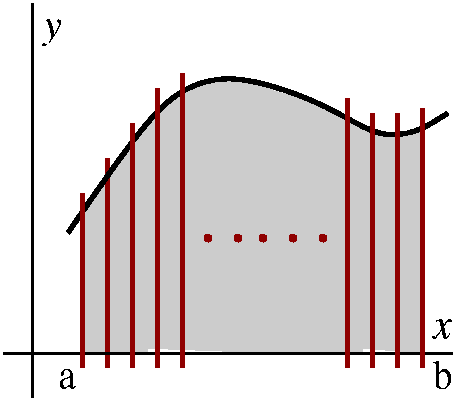 How to approximate area
How to approximate area
Suppose that we have a function, f, defined on an interval [a,b] and
we want to compute the area under y=f(x). That's the area bounded by
the x-axis (y=0) and the lines x=a and x=b on each side, and by the
curve y=f(x) on top.
We can get approximations to the area of by dividing the interval into n equal parts (people don't always use equal parts, but we're just starting out!). Then we can look at "sample points" in each subinterval, compute f's value at those sample points, and multiply those heights by the widths of the subinterval to get areas of rectangles. Then (sigh!) finally take the sum of these rectangles, and that will be an approximation to the area we want to compute.
The textbook explains in detail how to write the approximating sums. In particular, it identifies three sums corresponding to three choices of sample points: left and right endpoints of subintervals, and the midpoints of subintervals. Below are the formulas, which you should not memorize, and what are supposed to be pictures of a piece of the graph of y=f(x) over (relatively) tall and (relatively) narrow subintervals with the areas of the relevant boxes displayed. Since the interval has length b–a, the width of each subinterval is {b–a}/n. Do not memorize but do try to understand.
| Left-hand endpoints of subintervals |
(∑j=1nf(a+[{j–1}{b-a}/n]))({b–a}/n) | 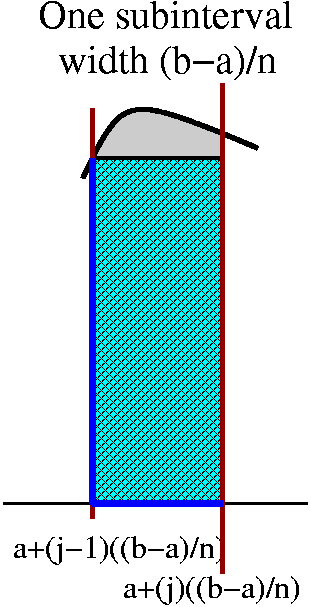 |
| Right-hand endpoints of subintervals |
(∑j=1nf(a+[{j}{b-a}/n]))({b–a}/n) | 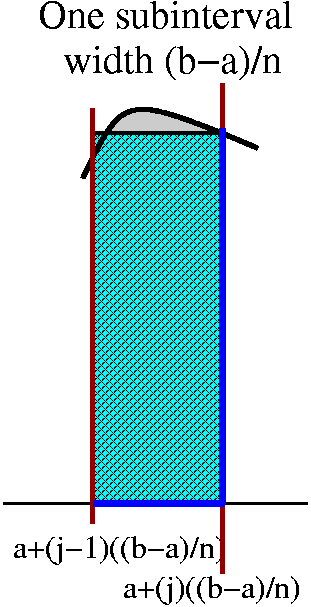 |
| Midpoints of subintervals |
(∑j=1nf(a+[{j–1}{b-a}/n+(1/2){b-a}/n]))({b–a}/n) | 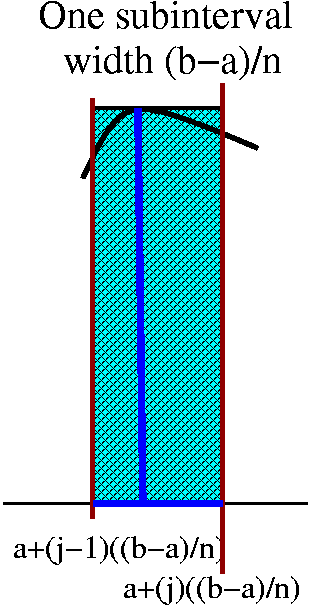 |
QotD
I don't remember! I think it was something like "Compute ∑j=13(j+{2/j})".
| Tuesday, November 10 | (Lecture #20.5) |
|---|
Antiderivatives
A function F is an antiderivative of f if F´=f. I
think the name itself is almost the definition. This turns out to be a
very useful concept. It has accumulated other names. For example, F is
also called an indefinite integral of f. The word "primitive"
is also used, as in, "F is a primitive of f".
|
Example I think we should begin with a very simple example. Look at f(x)=x–3, quite simple. Then F(x)=(1/2)x2–3x is an antiderivative of f. Why it this true? Well, just compute the derivative of F. The 2 in the exponent moves down, and cancels the 2 in the 1/2. And –3x differentiates to –3. So the claim is verified. Actually (and this is useful to note!), you can always verify a claim that F is an antiderivative of f by just differentiating. Some qualitative aspects of even this "simple" example are worth noticing. The line is negative to the left of x=3, so the parabola (which happens to have roots at 0 and 6) must be decreasing to the left of x=3. The line is positive to the right of x=3, and there the parabola is increasing. Certainly, when x=3, the parabola must have a minimum, because to the left its derivative is negative and to the right its derivative is positive. The transition in first derivative sign from – to + indicates a local minimum (First Derivative Test). | 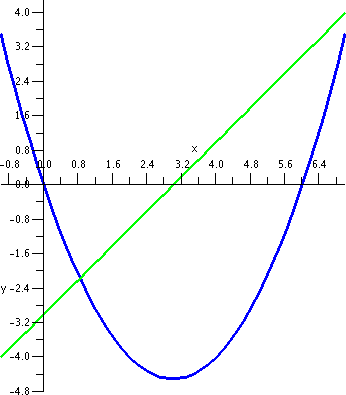 |
|
More example and discussion Well, as several (more than several, actually) tried to tell me, there are other antidervatives. For example, (1/2)x2–3x+2 is also an antiderivative of f(x)=x–3. The graph now to the right I hope shows y=(1/2)x2–3x+2. It is the original parabola shoved up. I hope that you notice it has the same qualitative ({in|de}creasing) properties in the same intervals as the original parabola. And we could push the parabola down (I think y=(1/2)x2–3x–1.75 is displayed). Etc. What does this "Etc." mean here?
+C | 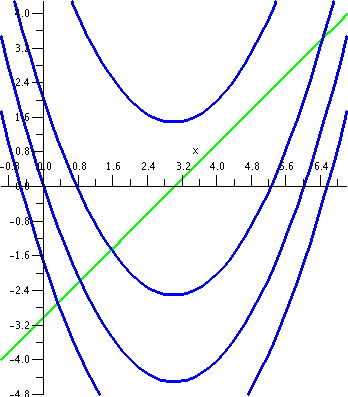 |
Here is a first very brief list of antiderivatives. This information is obtained just be reversing some derivative formulas. Please notice that if you don't believe a given formula, you can always differentiate and check. Also, the "+C" is generally omitted from tables of this type because it takes room and "one" should know it is there.
| Function | An antiderivative |
|---|---|
| xn, n not equal to –1 | (1/[n+1])x |
| 1/x | ln(x) |
| sin(x) | –cos(x) |
| cos(x) | sin(x) |
| ex | ex |
| There will be many more entries! | |
Notation
There is special notation for antiderivatives. For reasons which are
not clear now but which will be clear (I hope!) in about two
weeks, and which come from hundreds of years ago (really, this
notation is an abbreviation of a Latin word) we would write the
phrase, "F(x) is an antiderivative of f(x)" as ∫f(x) dx=F(x)+C. So, for example,
∫3ex+x5dx=3ex+(1/6)x6+C.
Example and vocabulary
A function can certainly have many antiderivatives (hey, if it has
one, it must have infinitely many!). So how can we separate the
various antiderivatives? The idea and the vocabulary come from simple
physical considerations, where the derivative is velocity and the
function is position (and x represents time). If the velocity is
prescribed, then we should be able to tell where the object is if the
starting position is given.
So this is the idea of an initial value problem. A differential equation is given for an "unknown" function, and then some value of the unknown function is given at some value of its argument (the initial condition). Let's look at a simple example.
Initial Value Problem
Differential equation
y´=2x7+8x.
Initial
condition y(1)=3.
Since y´=2x7+8x I know (consult the table above) that
y must be (2/7)x8+4x2+C. I put in the
"+C" so that all possibilities for y are covered. Now plug in x=1 and
set this equal to the given value of y. We get: (2/7)+4+C=3, so
C=3–4–(2/7)=–(9/7). The particular solution, the one specific solution
for this initial value problem is therefore
y=(2/7)x8+4x2–(9/7).
The idea here is that the differential equation tells how a quantity changes or evolves (?) with respect to its independent variable, and that giving a starting value together with a description of the rate of change should be enough to deduce the value of the quantity at any other time. Of course, whether or not this is practical or gives any useful information is something we need to investigate. Here is a very direct version of this idea: if you tell me that my weight last January 1st was 180 lbs, and then you keep track of, say, my monthly gains and losses, you certainly should be able to tell my weight at the end of the year.
Superman
Suppose that Superman leaps straight up at 40 ft/sec from the top of a
20 ft tall hill. What is his maximum height, and when does he get
highest? In this case, the presumed gravity of earth pulls down
and we will say that g is –32 ft/sec2.
It was my feeling that most students know how to do a problem like this using formulas, and I wanted to plod through it principally as a way of checking our vocabulary.
Translation
Let's measure height from ground level in feet, with + meaning above
ground level. And we will measure time in seconds from when Superman
jumped. What do we know? There are facts about three functions,
and confusion is easy.
Solution
Comments on this problem and its solution
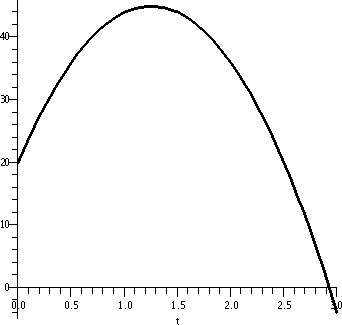 This is not a difficult problem, and I am sure that lots of formulas memorized for physics can be used to get the answers. I want to be sure that you understand the language and the process, so that more interesting problems can be analyzed successfully.
This is not a difficult problem, and I am sure that lots of formulas memorized for physics can be used to get the answers. I want to be sure that you understand the language and the process, so that more interesting problems can be analyzed successfully.
The graph to the right has time in seconds as the horizontal axis and has height in feet as the vertical axis. The units differ. I plotted the height functon for the time interval [0,3]. My Superman has somehow landed below ground level on his flight. Oh well. In fact, I think my Superman would hit the darn hill he leaped from (unless someone else has moved it during his flight) at time 2.5. I've never found this sort of problem too believable.
|
Car acceleration So I need to buy a car. One car I am thinking about goes from 0 to 60 mph in 9.5 seconds. How many g's (g is acceleration of gravity) is this? How can we set this up as a differential equation problem? Again, right now, I am more interested in the process than the answer. Well, 60 mph is 88 feet per second. Assume we begin at t=0 seconds, with both position and velocity equal to 0: s(0)=0 and v(0)=0. We know that v(9.5)=88. Also assume acceleration is constant, so a(t)=K. Now v(t)=Kt+C, and (using v(0)=0) we get v(t)=Kt. Since v(9.5)=88, I see that K(9.5)=88, and K=88/9.5, approximately 9.263. Now g (in these units) is 32, so this car accelerates (for this task) at 9.263/32, approximately .289 g. And then I wondered what distance the car takes to get to 60 MPH, surely a relevant safety question. For this we need to know s(t). But s(t)=(1/2)Kt2+C, and again C–0 (since s(0)=0). So s(9.5)=(1/2)(9.263)(9.5)2, about 417.993 ft, or a bit less than a tenth of a mile (hey, more than a football field). This car's list price is $16,500. Now another car surely which should be bought by a faculty member will go from 0 to 60 in 3.4 seconds. Let's go through the numbers: K(3.4)=88, so this K is 25.882, and g is 25.882, about .81 g. Huh: about three times the acceleration. And the distance needed to get to 60 mph is s(3.4)=(1/2)(25.882)(3.4)2, about 150 feet, half the length of a football field. This list price of this reasonable vehicle is $123,600. Indeed. Which should I buy? |
Maintained by greenfie@math.rutgers.edu and last modified 11/17/2009.