Math 152 diary, spring 2009: third section
Earlier material
Much earlier material
In reverse order: the most recent material is first.
| Monday,
May 4 | (Lecture #26) |
|---|
Today we concentrate on calculus in polar coordinates. I'll first
sketch some "classical" polar coordinate curves, and then I'll do some
computations with arc length and area. In class I did examples with
cosine. Here are similar examples with sine.
A collection of examples
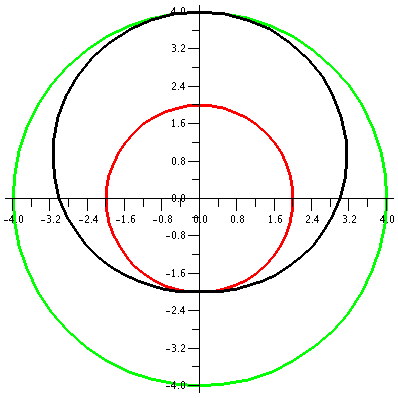
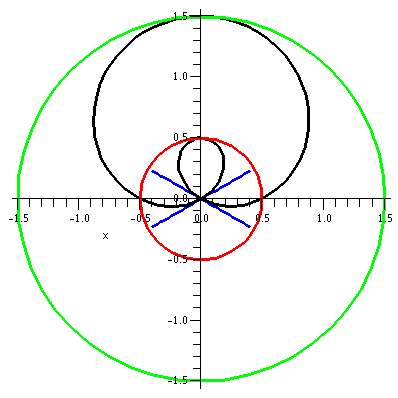
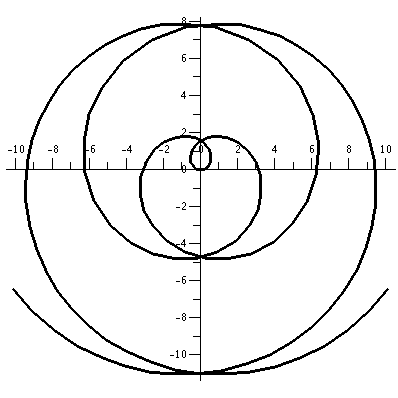
r=3+sin(θ)
Let's consider r=3+sin(θ). Since the values of sine are all
between –1 and 1, r will be between 2 and 4. Any points on this curve
will have distance to the origin between 2 and 4 (the green and red
circles on the accompanying graph). When θ=0 (the positive
x-axis)
r is 3. As θ
increases in a counterclockwise fashion, the value of r increases to 4
in the first quadrant. In the second quadrant, r decreases from 4 to
3. In the third quadrant, corresponding the sine's behavior (decrease
from 0 to –1) r decreases from 3 to 2. In all of this {in|de}crease
discussion, the geometric effect is that the distance to the origin
changes. We're in a situation where the central orientation is what
matters, not up or down or left or right. Finally, in the fourth
quadrant r increases from 2 to 3, and since sine is periodic with
period 2Π, the curve joins its earlier points.
The picture to the right shows the curve in black. I'd describe the
curve as a slightly flattened circle. The flattening is barely
apparent to the eye, but if you examine the numbers, the up/down
diameter of the curve is 6, and the left/right diameter is 6.4.
| 
|
Converting to rectangular coordinates
A naive person might think, "Well, I could convert the equation
r=3+sin(θ) to rectangular coordinates and maybe understand it
better." Except under rare circumstances (I'll show you one below),
the converted equation is very irritating and difficult to
understand. For example, Let's start with r=3+sin(θ) and
multiply by r. The result is r2=3r+r·sin(θ). I
multiplied by r so that I would get some stuff I'd recognize from the
polar/rectangular conversion equations. r2 is
x2+y2 and r·sin(θ) is y. So I have
x2+y2=3r+y, or
x2+y2–y=3r. I would rather avoid square roots so
I will square this, and get
(x2+y2–y)2=9r2=9(x2+y2).
This is a polynomial equation in x and y of highest degree 4, defining
this curve implicitly. I don't get much insight from this.
|
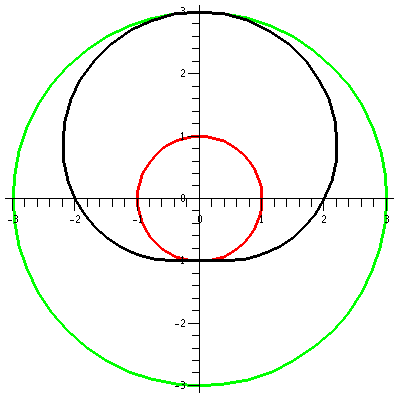
r=2+sin(θ)
Now consider r=2+sin(θ). Again,
the values of sine are all between –1 and 1, so r will be between 1
and 3. Any points on this curve will have distance to the origin
between 1 and 3. We can begin (?) the curve at θ=0 when r=2, and spin around
counterclockwise. The distance to the origin increases to r=3 at θ=Π/2 (the positive y-axis). The
distance to the origin decreases back to r=2 when θ=Π (the negative x-axis). The
curve gets closest to the origin when θ=3Π/2 (the negative y-axis) when r=1. Finally, r increases
(as θ increases in the
counterclockwise fashion) to r=3 again when θ=2Π.
Here the "deviation" from circularity in the curve is certainly
visible. The bottom seems especially dented.
| 
|
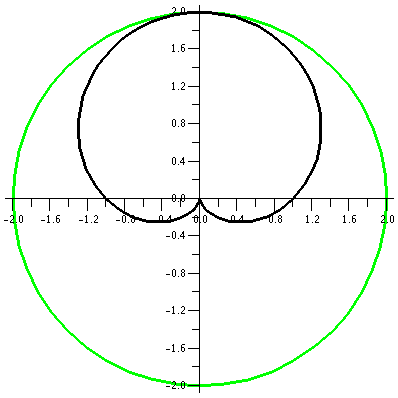
r=1+sin(θ)
We decrease the constant a bit more, and look at r=1+sin(θ). The values of sine are all
between –1 and 1, so r will be between 0 and 2. The (red) inner circle
has shrunk to a point. This curve will be inside a circle of radius 2
centered at the origin. We begin our sweep of the curve at 0, when r
is 1. Then r increases to 2, and the curve goes through the point
(0,2). In the θ interval from
Π/2 to Π, sin(θ) decreases
from 1 to 0, and the curves moves closer to the origin as r decreases
from 2 to 1. Something rather interesting now happens as θ travels from Π to 3Π/2 and then
from 3Π/2 to 2Π. 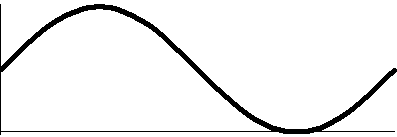 The rectangular graph of 1+sine, shown here, decreases
down to 0 and then increases to +1. The polar graph dips to 0 and then
goes back up to 1. The dip to 0 in polar form is geometrically a sharp
point! I used "!" here because I don't believe this behavior is easily
anticipated. The technical name for the behavior when r=3Π/2 is
cusp. The rectangular graph of 1+sine, shown here, decreases
down to 0 and then increases to +1. The polar graph dips to 0 and then
goes back up to 1. The dip to 0 in polar form is geometrically a sharp
point! I used "!" here because I don't believe this behavior is easily
anticipated. The technical name for the behavior when r=3Π/2 is
cusp.
This curve is called a cardioid from the Latin for "heart"
because if it is turned upside down, and if you squint a bit, maybe it
sort of looks like the symbolic representation of a heart. Maybe.
| 
|
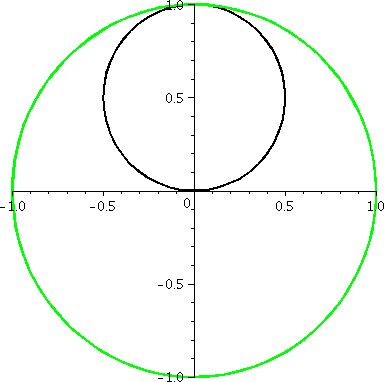
r=1/2+sin(θ)
Let's consider r=1/2+sin(θ). The values of sine are all
between –1 and 1, so r will be between –1/2 and 3/2. The (red) inner
circle actually had "radius" –1/2, and it consists, of course, of
points whose distance to the pole, (0,0), is 1/2. When θ is 0, r is 1/2. In the first two
quadrants, 1/2+sin(θ) increases
from 1/2 to 3/2 and then backs down to 1/2. In the second two
quadrants, when θ is between Π
and 2Π, more interesting things happen.
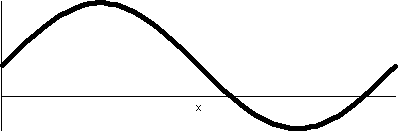 The rectangular graph on the interval [0,2Π] of sine moved up by 1/2
shows that this function is 0 at two values, and is negative between
two values. The values are where 1/2+sin(θ)=0 or sin(θ)=–1/2. The values of θ satisfying that equation in the
interval of interest are Π+Π/6 and 2Π–Π/6. The curves goes down to
0 distance from the origin at Π+Π/6, and then r is negative until
2Π–Π/6. The natural continuation of the curve does allow negative
r's, and the curve moves "behind" the pole, making a little loop
inside the big loop. Finally, at 2Π–Π/6, the values of r become
positive, and the curve links up to the start of the big loop.
The rectangular graph on the interval [0,2Π] of sine moved up by 1/2
shows that this function is 0 at two values, and is negative between
two values. The values are where 1/2+sin(θ)=0 or sin(θ)=–1/2. The values of θ satisfying that equation in the
interval of interest are Π+Π/6 and 2Π–Π/6. The curves goes down to
0 distance from the origin at Π+Π/6, and then r is negative until
2Π–Π/6. The natural continuation of the curve does allow negative
r's, and the curve moves "behind" the pole, making a little loop
inside the big loop. Finally, at 2Π–Π/6, the values of r become
positive, and the curve links up to the start of the big loop.
This curve is called a limaçon. The blue lines are lines with
θ=Π+Π/2 and θ=2Π–Π/6. These lines, for the θ
values which cross the pole, are actually tangent to the curve at the
crossing points.
| 
|
r=0+sin(θ)
Let's try a last curve in this family, with the constant equal to
0. What does r=sin(θ) look like? A graph is shown to the right.
There are several interesting features of this graph. First, this is a
polar curve which does have a nice rectangular (xy) description. If we
multiply r=sin(θ) by r, we get
r2=r·sin(θ), so that
x2+y2=y. This is x2+y2–y=0
or, completing the square,
x2+y2–2(1/2)y+(1/2)2–(1/2)2=0
so that (x–0)2+(y–1/2)2=(1/2)2. This
is a circle of radius 1/2 and center (0,1/2), exactly as it looks.
The moving "picture" of this curve is quite different. Between
0 and π it spins once around the circle but then from π to 2π
it goes around the circle another time! So this is really somehow two
circles, even though it looks like only one geometrically.
| 
|
More information about these curves is available here
Length of polar curves
The formula is
∫θ=αθ=βsqrt(r2+(dr/dθ)2)dθ. This formula is gotten from the parametric
curve formula on p.652 of the textbook. I used it to find the length of the
cardioid (the double angle formula from trig is needed). Then I
used it to find the length of a circle (!), but here the novelty is
that we actually trace the circle r=cos(θ) twice from 0
to 2π, so some care is needed if we only wanted to find the length
of one circumference.
"Sketching" roses
Here are dynamic pictures of two roses. The first is the one I
sketched in class r=cos(3θ). It is covered twice and has 3
"petals". The second is r=cos(4θ). It is only covered once, and
it has 8 petals! Wow, polar coordinates can be annoying!
r=cos(3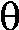 )
This is a three-leafed rose. Please note that the graph shows one
sweep, as θ goes from 0 to 2Π. )
This is a three-leafed rose. Please note that the graph shows one
sweep, as θ goes from 0 to 2Π. 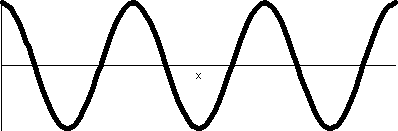 The rectangular graph, shown here, has three pairs of ups
and downs. The polar trace covers the leaves twice. The six
up-and-downs of cos(3θ) (magically?) reduce to retracings of
half of the loops. I hope I made this evident. I
introduced some deliberate distortion in the second
tracing. (!) Without the distortion, the second tracing
could not be seen at all. The imaginary "point" travels over the
computer screen's pixels and colors them (from white to black in this
case). The second trip could not be noticed since the pixels had
already been flipped to black. So I put in a small perturbation so
that the second layer of travel could be seen. The rectangular graph, shown here, has three pairs of ups
and downs. The polar trace covers the leaves twice. The six
up-and-downs of cos(3θ) (magically?) reduce to retracings of
half of the loops. I hope I made this evident. I
introduced some deliberate distortion in the second
tracing. (!) Without the distortion, the second tracing
could not be seen at all. The imaginary "point" travels over the
computer screen's pixels and colors them (from white to black in this
case). The second trip could not be noticed since the pixels had
already been flipped to black. So I put in a small perturbation so
that the second layer of travel could be seen.
| 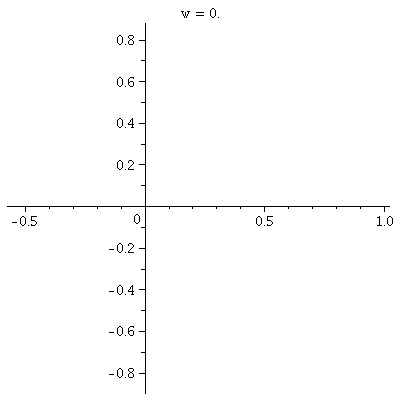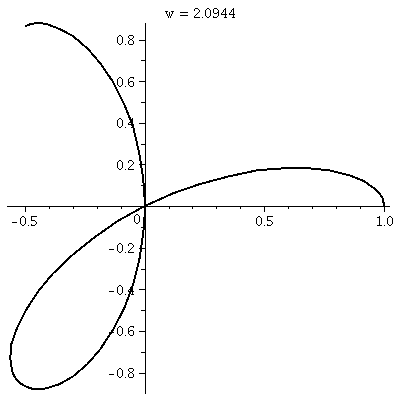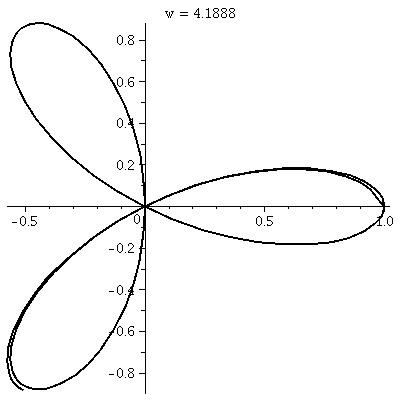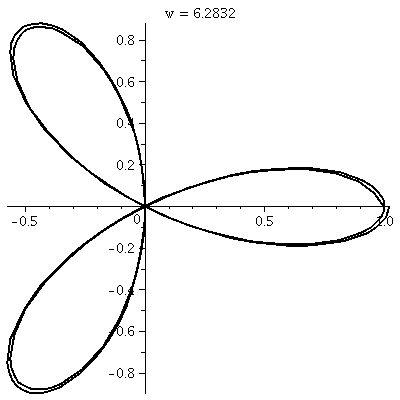
|
r=cos(4θ)
This "rose" has 8 leaves or petals, and
the dynamic way it is traced is weird and wonderful to me. 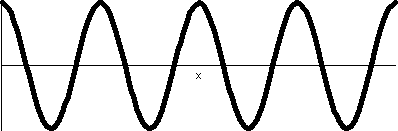 The rectangular
graph. to the right, shows four bumps up and four bumps down. There
are no retracings of already colored points, so that the wiggles up
and down of cos(4θ) all result in 8 leaves. The rectangular
graph. to the right, shows four bumps up and four bumps down. There
are no retracings of already colored points, so that the wiggles up
and down of cos(4θ) all result in 8 leaves.
| 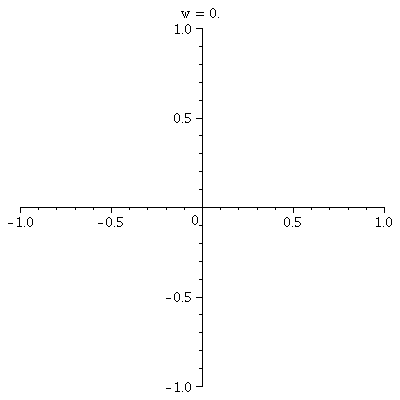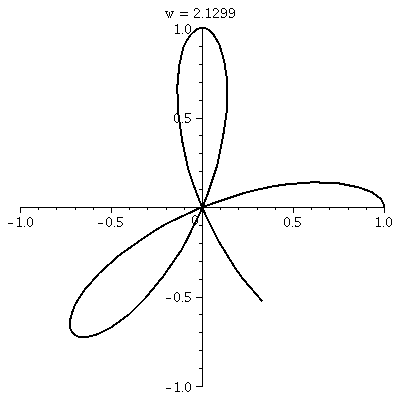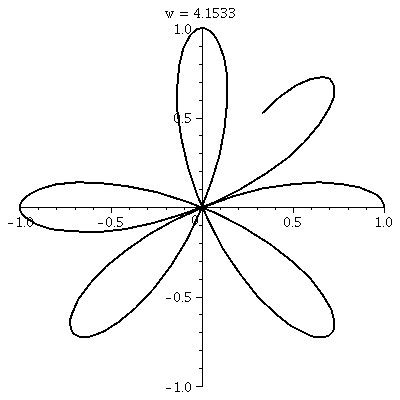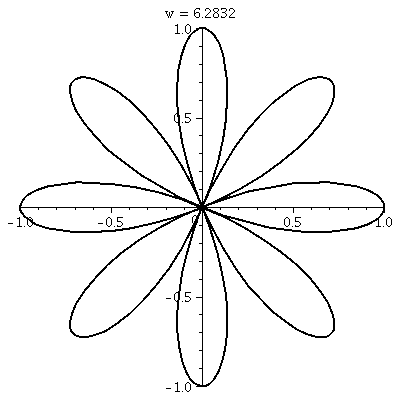
|
Area inside one petal of r=cos(3θ)
Well, cos(3θ) "first" (going from 0 to 2π) is 0 when
3θ=π/2. So we get half a petal by integrating from 0 to
π/6. The formula is
∫αβ(1/2)r2dθ for
area in polar coordinates (see the discussion on p.649 of the
textbook), so this becomes (for the whole petal, we need to
double):
2·(1/2)∫0π/6
cos(3θ)2dθ. This can be computed using a trig
identity.
| 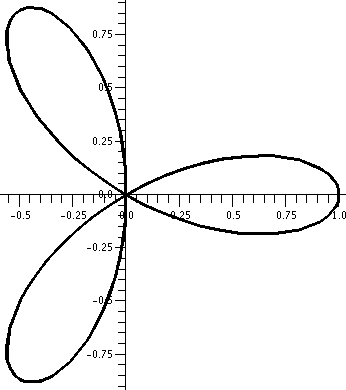 |
QotD
Has the QotD been helpful to you? This is the last QotD and
won't be returned. I would be interested in your opinion, really.
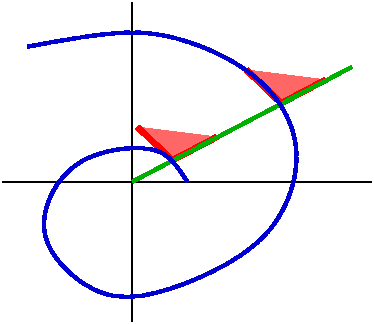
Another kind of spiral
I didn't talk about Exponentials and snails, darn it! Curves
of the form r=a ebθ are spirals of a different
kind than what we've drawn (for example, different from the spiral
drawn for the QotD last time). All of these spirals have a strange and
wonderful geometric property. If a ray is drawn from the pole (the
origin) then the angle the ray makes with the tangent line of the
spiral at any intersection is the same. I attempted to
illustrate this with the first picture to the right. It turns out that
this silly geometric property has natural consequences in terms of the
energy efficiency of its construction. A snail shell when considered
transversal (perpendicular) to the axis of symmetry usually is one of
these curves. You can read a wikipedia
article about these spirals, which have a number of different
names (of course!).
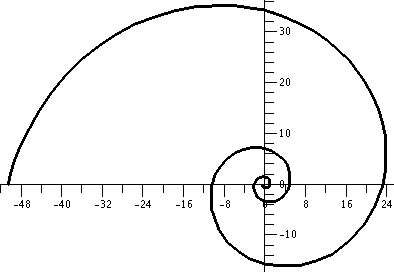
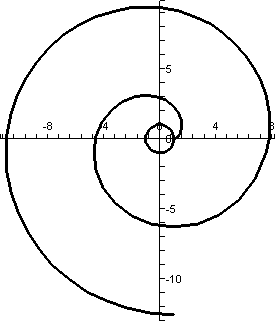
To the right is a machine-drawn picture of r=e.25θ
as θ goes from
–Π to 5Π. The .25 was put in to make the exponential not
grow too fast so the picture would be tolerable.
|
|
| Wednesday,
April 29 | (Lecture #25) |
|---|
Please "recall" these calculus results about parametric curves. (The
quotes are around that word because I didn't really cover the formulas
very well last time.)
Slope
dy dy/dt
-- = -----
dx dx/dt
Speed
Speed=sqrt(f´(t)2+g´(t)2) or
___________
/(dx)2 (dy)2
Speed= / (--)+ (--)
/ (dt) (dt)
As you'll see if you take Math 251,
this is the sum of the squares of the
horizontal and vertical components of the velocity vector: it is,
in fact, the magnitude of the velocity vector.
Length of a curve
Well, suppose we move along a parametric curve given by x=f(t) and
y=g(t) from t=START to t=END. If we believe that the
speed is sqrt(f´(t)2+g´(t)2), then we
know that this speed can vary. In a sort time interval (dt long!) the
distance traveled is Speed·Time, or
sqrt(f´(t)2+g´(t)2)dt. We can add up
all these distances from t=START to t=END using the
integral idea. So the distance traveled along the curve from
t=START to t=END will be given by
∫t=STARTt=ENDsqrt(f´(t)2+g´(t)2)dt.
(We are integrating the magnitude of the velocity vector). Is this a
reasonable formula?
Almost no speed functions have nice, neat, simple antiderivatives. In
the real world, you'll need to use numerical approximation. However,
Math 152 is not the real world.
A textbook problem
Section 11.3, problems 3 through 15, are all "Find the length of the
path over the given interval" with some rather silly-looking functions
specified. Accidentally (exactly not accidentally, actually!)
all of the problems can be computed exactly with antiderivatives and
values of standard functions. There is a fair amount of ingenuity
involved in constructing such examples. I urged students to practice
with several of them. Here is problem #7:
Find the length of the path described by
(3t2,4t3), 1≤t≤4.
The solution
Here x=3t2 and y=4t3. We will compute the speed
and then attempt to "integrate" (actually using FTC, so we'll need to
find the antiderivative). Now dx/dt=6t and
dy/dt=12t2. Therefore the speed is sqrt(6t)2+(12t2)2). This is
sqrt(36t2+144t4). We'll need to integrate this,
and maybe I will "simplify" first. Indeed, since we consider t in an
interval where t≥0, sqrt(t2)=t (otherwise we would need
to worry about |t| or –t etc.). But
36t2+144t4=36t2(1+4t2) so
that the square root is 6t·sqrt(1+4t2). Therefore
the distance traveled along the curve is an integral,
∫t=1t=46t·sqrt(1+4t2)dt.
Several students immediately suggested various substitutions. Here is
one which does the job efficiently. So:
If u=1+4t2, du=8t dt, so (1/8)du=dt.
∫6t·sqrt(1+4t2)dt=(6/8)∫sqrt(u)du.
Now
(6/8)∫sqrt(u)du=(6/8)(2/3)u3/2+C=(1/2)u+C=(1/2)(1+4t2)3/2+C.
So
∫t=1t=46t·sqrt(1+4t2)dt=(1/2)(1+4t2)3/2|14=(1/2)(65)3/2–(1/2)(5)3/2.
A tangent line to the evolute
Let me find a tangent line to the evolute of a circle (the path of the
bug, discussed last time) when t=3Π/4. For this,
x(t)=cos(t)+t sin(t) and y(t)=sin(t)–t cos(t). When
t=3Π/4, x=–[1/sqrt(2)]+3Π/sqrt(2) (approximately 0.95897)
and y=[1/sqrt(2)]+3Π/sqrt(2) (approximately 2.37319). So we know a
point the line goes through. How about the slope?
dy/dx=(dy/dt)/(dx/dt)=[cos(t)–cos(t)+t sin(t)]/[–sin(t)+sin(t)+t cos(t)]=tan(t)
(amazing that it is so relatively simple). At t=3Π/4, this is
–1. So the line is
y–[1/sqrt(2)]+3Π/sqrt(2)=(–1)(x–{–[1/sqrt(2)]+3Π/sqrt(2)}). The
line and the curve are shown to the right.
| 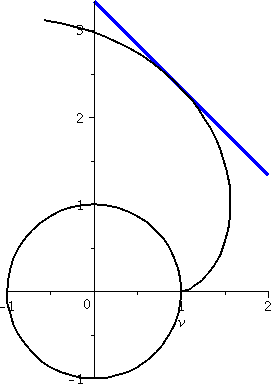 |
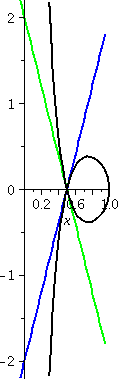 Tangent lines
Tangent lines
I'll find the tangent lines at the self-intersection point of my favorite curve. The point involved is (1/2,0) and
the two values of t are +1 and –1. Since I have the point, the other
information I need to find the tangent lines is the slope. Well, slope
is dy/dx=(dy/dt)/(dx/dt).
Since x=1/(1+t2),
dx/dt=(–2t)/(1+t2)2. I only fouled this up two
or three times in class, but when t=–1, dx/dt=1/2, and when t=+1,
dx/dt=–1/2.
Since y=t3–t, dy/dt=3t2–1. When t=–1 or when
t=+1, dy/dt=3–1=2.
Therefore when t=–1, dy/dx=(2)/(1/2)=4. The line goes through (1/2,0),
so an equation for it is y=4(x–1/2).
Therefore when t=1, dy/dx=(2)/(–1/2)=–4. The line goes through (1/2,0),
so an equation for it is y=–4(x–1/2).
I had Maple graph the parametric curve
and the two lines just found (in green and
blue). I then asked what the angle between the
lines (the angle which encloses the x-axis). The angle is 151.9
degrees. Hey, please remember that the slope of a line is the tangent
of the angle that the line makes with the positive x-axis. Here the
angle between the
line y=4(x–1/2) and the positive x-axis has angle equal to arctan(4),
approximately 1.326 radians. Double this is about 151.9 degrees. Hey:
we have the machines. Please use them.
Uniform speed?
We developed a formula for speed. It was
sqrt(f´(t)2+g´(t)2) where x=f(t) and
y=g(t). For the circle x=5cos(t) and y=5sin(t), previously considered, we know dx/dt=–5sin(t) and
dy/dt=5cos(t), so that (dx/dt)2+(dy/dt)2=25((sin(t))2+(cos(t))2)=25·1=25, so the speed, which is the square
root, is always 5. So this is uniform circular motion: the word
"uniform" here means that the speed is constant. (Notice, oh physics
people, that I am not saying the velocity is constant and I am not
saying that the acceleration is 0. Indeed, both of those statements
are false. The direction of the velocity is changing, so the
acceleration is not 0. We need to look at these quantities as
vectors, and this will be done in Math 251.)
Nonuniform speed
Then I tried to analyze an ellipse we had parameterized
earlier. We have x(t)=5cos(t) and y(t)=3sin(t) so
dx/dt=–5sin(t) and dy/dt=3cos(t), and the speed is the square
root of 25(sin(t))2+9(cos(t))2=
16(sin(t))2+9(sin(t))2+9(cos(t))2=
16(sin(t))2+9 since sin2+cos2 is
1. Sigh. The speed at time t is sqrt(16(sin(t))2+9). When
t=0, the particle whose motion we are describing is at (5,0) and the
speed is sqrt(9)=3 since sin(0)=0. When t=Π/2, the particle is at
(0,3) and the speed is sqrt(25)=5 since sin(&pi/2)=1. So certainly the
particle is not moving at the same speed. Indeed, a graph of the
speed, sqrt(16(sin(t))2+9), is shown to the right.
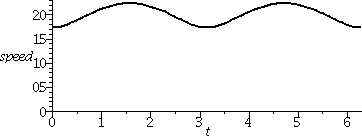 Now this does resemble what I know about the motion of a planet in
orbit. When it is far away from the center of the orbit, the planet
will have large potential energy and relatively small kinetic energy
(it will move slowly). This is near t=0 and t=Π. When it is close
to the center of the orbit, the planet moves faster, and the kinetic
energy is larger, while the potential energy, measured by the work
needed to move closer/farther from the center, decreases.
Now this does resemble what I know about the motion of a planet in
orbit. When it is far away from the center of the orbit, the planet
will have large potential energy and relatively small kinetic energy
(it will move slowly). This is near t=0 and t=Π. When it is close
to the center of the orbit, the planet moves faster, and the kinetic
energy is larger, while the potential energy, measured by the work
needed to move closer/farther from the center, decreases.
The total energy is conserved, but the way the total is divided
between kinetic and potential energy varies. Maybe if you look
again at the moving picture, you will "see" both of these
phenomena. They are not too clear to me visually.
Back to my favorite curve
The length of the loop in my favorite curve can be gotten by computing
the integral of the speed from –1 to +1 (the two self-intersection
times). So this is (I'll use the formulas we already have)
∫–11sqrt((–2t/(1+t2)2)2+(3t2–1)2)dt.
Maple takes more than half a second
(quite a lot of time!) to acknowledge that it can't find an
antiderivative, so we can't use FTC. In less than a tenth of a second,
the approximate value 1.971944073 is reported.
|
A tilted ellipse
To the right is a graph of the parametric curve
x=sqrt(3)sin(t)+(1/2)cos(t)
y=–sin(t)+(sqrt(3)/2)cos(t)
for t between 0 and 2Π. As you might expect, this is a
prepared (non-random!) example. It is a rotated ellipse with
2-to-1 ellipticity. Those of you who take linear algebra (Math 250)
will be able to construct examples like this easily.) One thing which
turns out to be important in computer typesetting (typography) and,
more generally, computer graphics, is the idea of a bounding
box: the smallest box with vertical and horizontal sides
containing the figure. I would like to find the bounding box for this
curve. I will admit that in the real world, if I had just one curve, I
would probably just guess numerically -- I would "eyeball" it. But I
would like to show you a more systematic way to obtain the bounding
box.
| 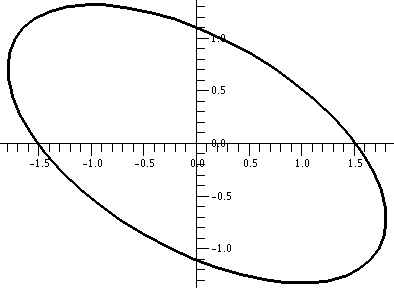 |
The top border
To find the top border, we must look for a
place where the tangent line is horizontal. This means that the
derivative should be 0. But we now know that
dy/dx=(dy/dt)/(dx/dt). This will be 0 if the top is 0 (hey, I am
neglecting the possibility that the bottom is 0 also but that doesn't
happen here and rarely should happen in practice). But
y=–sin(t)+(sqrt(3)/2)cos(t) so dy/dt=–cos(t)–(sqrt(3)/2)sin(t) so this
is 0 when tan(t)=2/sqrt(3). There isn't a simpler answer (!!!),
sorry. Even in such an easy example, the numerics get complicated. The
approximate numerical value of t is.85707. The point corresponding to
this value of t is (–(3/14)sqrt(21),(1/6)sqrt(63)) or approximately
(–.98189,1.32288). This is where the red line touches the ellipse in
the picture to the right.
|
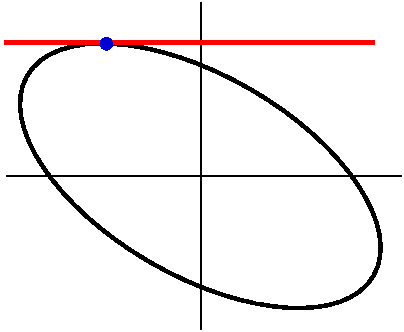 |
The right border
How about the right border? How could we find the point which is most
to the right on this tilted ellipse? We could look for a vertical
tangent. Since the slope of the tangent line is still given by
dy/dx=(dy/dt)/(dx/dt) the points which will be candidates for vertical
tangent lines will have dx/dt=0. (You see, looked at the correct way,
the "tilt" or direction of the tangent line is not quite the same as m
in y=mx+b. There's a better way to think about this, and this better
way will be shown to people in Math 251. Well,
x=sqrt(3)sin(t)+(1/2)cos(t) so dx/dt=sqrt(3)cos(t)–(1/2)sin(t) and
this is 0 if tan(t)=2sqrt(3) so that t=arctan(2sqrt(3)). There isn't a
simpler answer (!!!), sorry. Even in such an easy example, the
numerics get complicated. The approximate numerical value of t is
1.28976. The point corresponding to this value of t is exactly
(sqrt(13)/2,–(3/26)sqrt(39)) or approximately (1.80278,–.72058). And
that pair of numbers designates the blue point in the picture to the
right here.
|
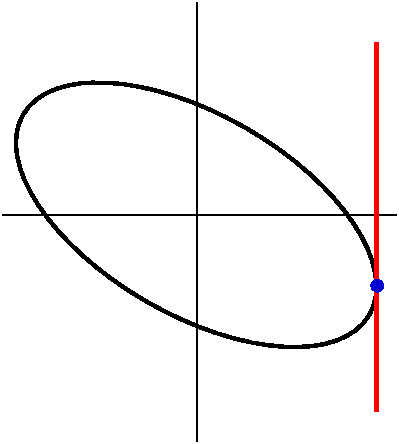
|
The bounding box
The numbers for the two blue points shown allow us to deduce the
vertices of the bounding box for this tilted ellipse. For example, the
top side of the box is y=the second coordinate of the first point
found. The right side is x=the first coordinate of the second point
found. By symmetry we can get the other sides (I centered the ellipse
at the origin) and the coordinates of the corners can be deduced
fairly easily.
|
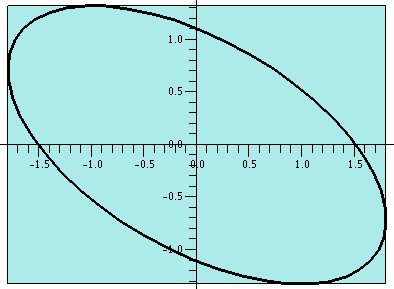
|
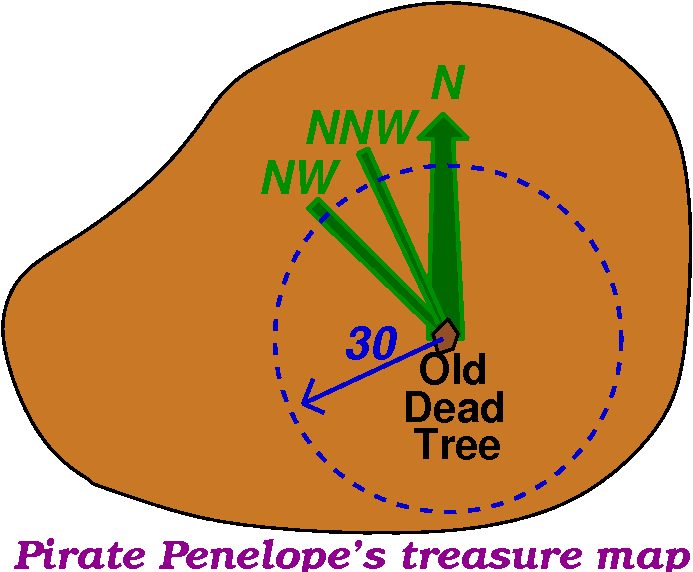 The idea of polar coordinates
The idea of polar coordinates
You have found a treasure map supposedly giving directions to the
burial spot of a chest full of gold, jewels, mortgages, etc., stolen
by the Dread Pirate Penelope. The information you have is that
A buried treasure is located 30 feet from the
old dead tree, in a
NorthNorthWest direction.
So there you are, on the island. Perhaps the Old dead tree is
still visible. You could mentally draw a circle 30 feet in radius
around the Old Dead Tree. Then you find the North
direction. π/4=45o to the West is NW (Northwest) and
then NNW (Northnorthwest) is π/8 towards North (anyway, you decide
on the direction). Where that direction intersects the circle is
probably where to dig, unless Penelope is tricky, etc.
The whole idea of located a point in a 2-dimensional setting using
distance from a fixed point and angle with respect to a fixed
direction is called polar coordinates.
"Standard issue" polar coordinates
Fix a point (usually called "the center" or sometimes "the pole" and
in most common situations, the origin of the xy-coordinate
system. Also fix a direction -- if needed this might be called "the
initial ray". Almost always this is the positive x-axis in an
xy-coordinate system. Then locate another point in the plane by giving
its distance from the center (called r) and by drawing the line
segment between the center and the point you are locating. Measure the
angle between that and the initial ray (note: counterclockwise is a
positive angle!): this is called θ. r and θ are the
polar coordinates of the point.
| 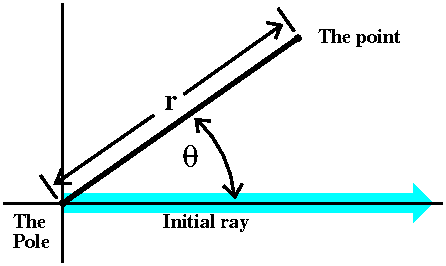 |
An example and the problem with polar coordinates
Well, make the standard choices for "the pole" and "the initial
ray". Let's get polar coordinates (the values of r and θ) for
the point whose rectangular coordinates are x=sqrt(3) and y=1. Of
course this is not a random point (sigh). So we consider the picture,
and decide that the hypotenuse (r) should be 2 units long, and the
acute angle (θ) should be π/6. Fine.
But suppose that the point (sqrt(3),1) is operating in a sort of
dynamic way. Maybe it is the end of a robot arm, or something, and
suppose that the arm is swinging around the pole, its angle
increasing. It might be true that we somehow are computing various
angles, and since the arm is moving continuously (still no teleporting
robot arms!) the angles which are θ's should change
continuously. If the arm swings completely around the pole, and comes
back to the same geometric location, it would make more sense to
report its polar coordinates as r=2 and θ=13π/6 (which is
better understood as 2π+π/6).
| 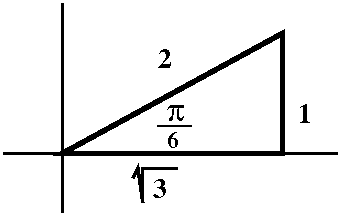
|
Some valid polar coordinates for the point whose rectangular
coordinates are x=sqrt(3) and y=1:
r=2 and θ=π/6 r=2 and θ=13π/6
r=2 and θ=25π/6 ETC.
But the "robot arm" could also swing around backwards, so other
possible polar coordinates for the same geometric point include
r=2 and θ=–11π/6 r=2 and θ=–23π/6
ETC.
Generally, r=2 and θ=π/6+2π(multiplied by any integer): the integer
could be 0 or positive or negative.
The irritation ("It's not a bug, it's a feature ...") is that there
are further "reasonable" polar coordinate pairs for the same point!
For example, go around to π/6+π. If you position your robot arm
there, and then tell the arm to move backwards 2 units, the arm will
be positioned at (sqrt(3),1). Sigh. So here are some more polar
coordinates for the same point:
r=–2 and θ=7π/6 and
r=–2 and θ=–19π/6
and r=–2 and θ=–31π/6 ETC.
but we are not done yet,
because there are also (going backwards in the angle and the
length)
r=–2 and θ=–5π/6 and
r=–2 and θ=–17π/6 and
r=–2 and θ=–29π/6 ETC.
Generally, r=–2 and θ=7π/6+2π(multiplied by any integer): the integer
could be 0 or positive or negative.
Common restrictions on polar coordinates and the problems they have
This is irritating. Any point in the plane has infinitely many valid
"polar coordinate addresses". In simple applications, people
frequently try to reduce the difficulty. Much of the time, we expect
r>0 always. And maybe we also make θ more calm. The
restriction 0≤θ<2π is used, except when it isn't, so
the restriction –π<θ≤π is used in other
circumstances. I am not trying to be even more incomprehensible than
usual. I am merely reporting what different people do. As we will see,
this is all very nice, except that there are natural circumstances,
both in physical modeling (the robot arm I mentioned) and in the
mathematical treatment, where it will make sense to ignore the
artificial restrictions, even if this makes life more
difficult. You'll see a few of these circumstances.
Conversion formulas
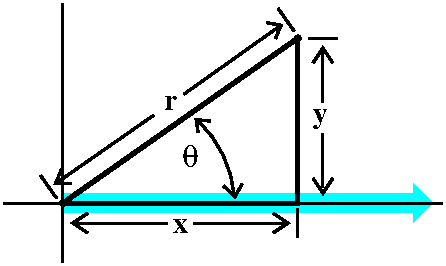 If you consider the picture to the right, I hope that you can fairly
easily "read off" how to go from r and θ to x and y:
If you consider the picture to the right, I hope that you can fairly
easily "read off" how to go from r and θ to x and y:
x=r cos(θ)
y=r sin(θ)
Going from x and y to r is easy enough:
r=sqrt(x2+y2). If we divide the y equation above
by the x equation, the r's drop out and we get y/x=tan(θ) so
that θ=arctan(y/x). Please note that there are infinitely
many valid r and θ pairs for every point, so this method
will only give you one such pair! Be careful in real applications,
please.
Specifying regions in the plane in polar fashion
It is useful to try to get used to thinking in polar fashion, because
then you will be able to see problems (usually physical or geometric
problems with lots of central symmetry) where this coordinate system
can be used to really simplify computations. So here are some simple
examples of regions which can be easily specified with polar
inequalities.
|
1<r<3
r=1 and r=3 represent two circles centered at 0, one of radius 1 and
one of radius 3. The inequality, which has no restriction on
θ, means that every point between these circles is in the region
specified. This sort of region is frequently called an annulus.
|
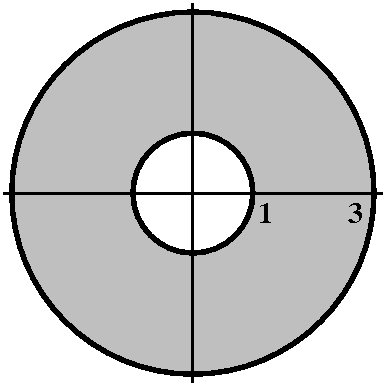
|
|
π/4<θ<π
Here there is no restriction on r. I will assume (!!) the standard
restriction that r should not be negative. Then a point is in this
region if its angle with respect to the positive x-axis is more than
π/4 and less than π (the angle π specifies the
negative x-axis!!!). I guess I would call this region a wedge.
I also "guess" that 0 is in this region. The wedge goes out radially
"to infinity" in all of the legal θ directions.
|
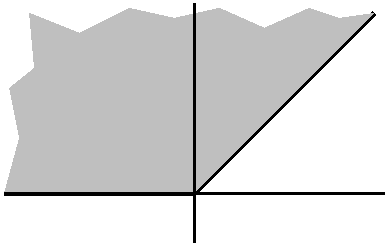
|
|
0<r<1 and π/2<θ<5&pi/4
Here are combined restrictions on both polar coordinates. I hope you
can "see" the geometric result. I could describe this region in
rectangular coordinates, certainly, but the needed equations and
inequalities would be much more complicated to me. Maybe this sort of
thing will give you some appreciation of the usefulness of polar
coordinates.
|
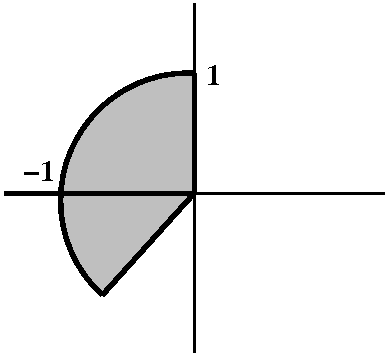
|
We will study the equations and graphs of some polar curves next time,
and we will do a bit of calculus (arc length and area). That will
conclude the course lectures.
Last QotD I can have returned
Please sketch as well as possible all points in the plane which have
r=θ using any (!) determination of polar coordinates (no
restrictions on r and θ). The result is weird until you get used
to it (as usual!). I will try to have the results returned on
Thursday, April 29.
To the right is Maple's graph of
r=θ when –12≤θ≤12. Think hard about
what the graph would look like for θ small positive (in the
first quadrant) and θ small negative (although the "robot arm"
is pointing in the fourth quadrant, the corresponding r value is
negative, so the curve appears in the second quadrant, near the
negative x-axis). The curve is smooth with no corners or cusps, and
has infinitely many self-intersections on the y-axis.
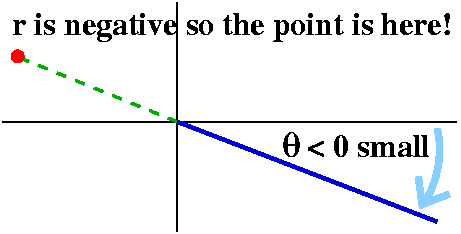
Most people got the θ>0 part of the curve right but the part
with θ<0 was incorrect, because it is difficult to remember
to go backwards when r is negative (this happens because the
curve is r=θ). I drew something like the
small picture to the left on some people's papers. I thought maybe
that might help them understand.
I don't think negative r's will occur very often in practice so maybe
this wasn't a great choice as QotD. This curve is an example of an
Archimedean
spiral (although usually r>0 in the description of that
spiral).
| Tuesday,
April 28 | (NOT a Lecture!) |
|---|
Mr. Schutz, a student in one of "our"
sections, wrote to me asking about hyperbolic functions because they
are mentioned in one of the section 11.2 homework problems. I had
vaguely mentioned these functions on Wednesday, March 4, in lecture
#12. The textbook has information about them (please use the entries
in the index). They are important functions, and their use will become
more pressing as you learn about differential equations. In an older
instantiation of Math 152, I wrote the following in a diary entry:
A curious collection of facts
I wrote parts of the table below, and added entries as I explained
them. So, for example, I defined sinh(x) (hyperbolic sine of x,
pronounced "cinch of x") as the difference
(1/2)[ex–e–x]. To get the series for this
function, I took the series for ex and substituted –x
for x. The result has minus signs at the odd powers. The difference of
the two series divided by 2 is the series shown. The function cosh(x)
(hyperbolic cosine of x, pronounced "cosh of x") is the average of
ex and e–x. Its series is half of the sum of the
series for each of the pieces. When the pieces are summed, the odd
powers cancel, and the result is what is shown.
The most intriguing (strange, weird?) entries in the table below occur
as a result of Euler's Formula. If you are willing to
accept that there is a number i whose square is –1, then something
strange happens as you consider eix. Notice that the powers
of i have this behavior:
i1=i and i2=–1 and
i3=i·i2=–i and
i4=i·i3=i·(–i)=(–1)(–1)=1 and
...
The powers of i repeat every four times. Therefore
eix=1+(ix)+(ix)2/2+(ix)3/6+(ix)4/24+...
eix=1+ix–x2/2–ix3/6+x4/24+...
The even terms are exactly like the series for cosine, and the odd
terms all have i, and except for that are like the series for
sine. So:
| Euler's Formula |
|
eix=cos(x)+i sin(x) |
Then because sine is odd and cosine is even,
e–ix=cos(x)–i sin(x). This gets the entries in the
formula column for sine and cosine (add and subtract the two
equations).
| Function | Formula | Differential equation
(actually,
the initial value problem) | Power
series |
|
sin(x) |
eix–e–ix
----------
2i |
y´´=–y
y(0)=0 and y´(0)=1
Simple harmonic
motion,
initial velocity sol'n |
x–x3/3!+x5/5!+... |
|---|
|
cos(x) |
eix+e–ix
----------
2 |
y´´=–y
y(0)=1 and y´(0)=0
Simple harmonic
motion,
initial position sol'n |
1–x2/2!+x4/4!+... |
|---|
|
sinh(x) |
ex–e–x
----------
2 |
y´´=y
y(0)=0 and y´(0)=1
|
x+x3/3!+x5/5!+... |
|---|
|
cosh(x) |
ex+e–x
----------
2 |
y´´=y
y(0)=1 and y´(0)=0
|
1+x2/2!+x4/4!+... |
|---|
There are other hyperbolic functions defined in a fashion which is
similar to trig functions. For example, the hyperbolic tangent, tanh
(pronounced ludicrously as "tanch") is sinh/cosh. As I previously
wrote, you may look in your textbook. But here also are some links:
A wikipedia
article;
A
MathWorld article.
Both of these are very technical and have too darn many formulas. A
slightly friendlier page is here.
There have been a few times in my life when I've done a lot of
computations with the hyperbolic functions. Then I somehow learned the
necessary formulas (sort of like the trig formulas, with fewer minus
signs!) and a few weeks later, I forgot them. Oh well.
|
| Monday,
April 27 | (Lecture #24) |
|---|
The final exam
The final exam for sections 1, 2, 3, 6, 7, 8, and 9 of Math 152
will be given in SEC 111 on Busch
campus from 4 to 7 PM on Thursday, May 7. This is
very soon. This link discusses
some review material.
We continue the schizophrenic (?) progression of this course by
spending three lectures on parametric curves and polar
coordinates. These topics would be better covered after other
applications of the definite integral, and I will use this order if I
teach this course again. Also, the material will make more sense from
the point of view of Math 251. Sigh. So, onwards.
Parametric curves
We begin our rather abbreviated study of parametric curves. These
curves are a rather clever way of displaying a great deal of
information. Here both x and y are functions of a parameter. The
parameter in your text is almost always called t. The simplest
physical interpretation is that the equations describe the location of
a point at time t, and therefore the equations describe the motion of
a point as time changes. I hope the examples will make this more
clear. The t here is usually described for beginners as time, but in
applications things can get a great deal more complicated. Parametric
curves could be used to display lots of information. I mentioned that
some steels contain chromium. Maybe the properties of the steel such
as ductility (a real word: "The ability to permit change of shape
without fracture.") and density, might depend on the percentage of
chromium. So the t could be that and the x and y could be measurements
of some physical properties of the steel. Here x=f(t) and y=g(t), as
in the text. Now a series of examples.
 Example 1
Example 1
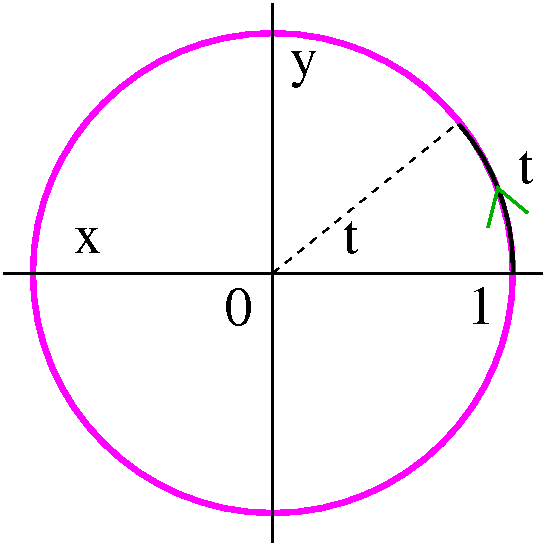
Suppose x(t)=cos(t) and y(t)=sin(t). I hope that you recognize almost
immediately that x and y must satisfy the equation
x2+y2=1, the standard unit circle, radius 1,
center (0,0). But that's not all the information in the equations.
The point (x(t),y(t)) is on the unit circle. At "time t" (when the
parameter is that specific value) the point has traveled a length of t
on the unit circle's curve. The t value is also equal to the radian
angular measurement of the arc. This is uniform circular
motion. The point, as t goes from –∞ to +∞, travels
endlessly around the circle, at unit speed, in a positive,
counterclockwise direction.
Example 2
Here is a sequence of (looks easy!) examples which I hope showed
students that there is important dynamic (kinetic?) information in the
parametric curve equations which should not be ignored.
- x(t)=t and y(t)=t. Surely the "particle" travels on the main
diagonal line y=x. The travel (remember, the domain unless otherwise
limited, is all values of t which makes sense to the defining
functions) is from lower left (third quadrant) to upper right, (first
quadrant). Also I hope that you see the particle moves at uniform
speed. This is uniform linear motion.
| 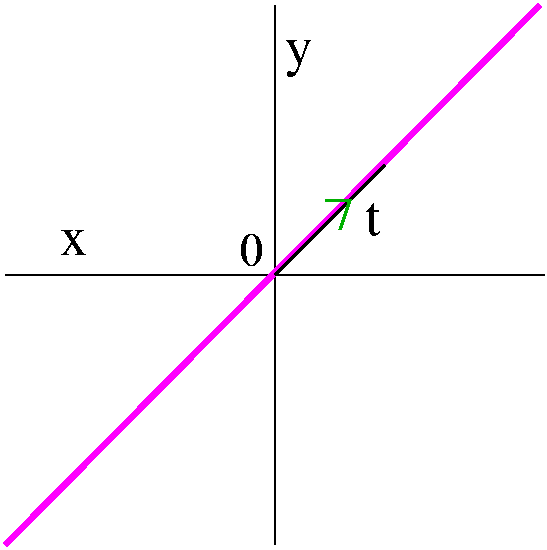
|
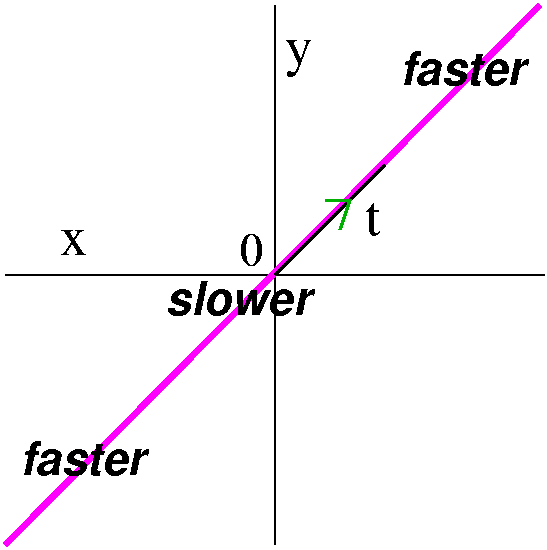
- x(t)=t3 and y(t)=t3. The path of this point
is also on the main diagonal line y=x. But the motion of this point,
while in the same direction as the first example (from third to first
quadrant), is very different. The difference is in the "clock". Try a
few values of t. Between t=0 and t=1 we travel from (0,0) to
(1,1). Between t=1 and t=2, we travel from (1,1) to (8,8). Just
roughly, the distance changes from sqrt(2) to sqrt(98). That's a big
change. The particle, near –∞, travels fast. Then as t goes
around 0, it is slower, and, as t gets very large positive, the
particle moves faster.
| 
|
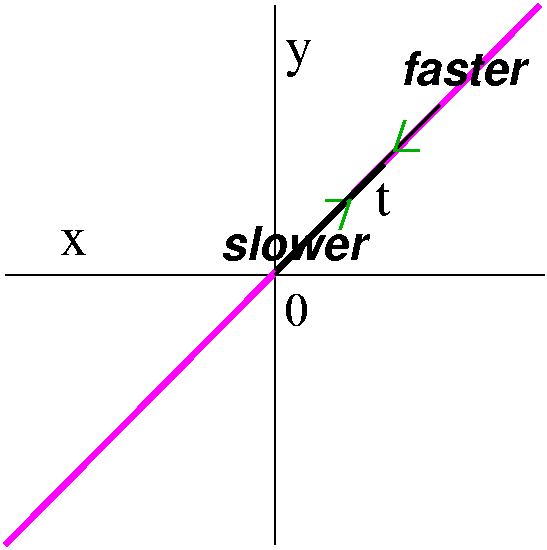
- Now let's consider the motion described by x(t)=t2 and
y(t)=t2. Again, we can "eliminate the parameter". That
rather grim phrase (if you read murder mysteries!) is what the text
uses to describe getting rid of t by manipulating the two
equations. Here we just realize that x=y. Much of the information
about the motion of this point on the main diagonal is lost if we go
to just y=x. The t2 means that both x and y must be
non-negative. When t is large negative, the point is way up high in
the first quadrant, and traveling towards the origin rather
rapidly. It begins to slow, and then "stops" (!) but only
"instantaneously" (!!) at (0,0) (when t=0). It turns around (how the
heck does a particle "turn around"?) and begins to retrace its path,
up towards the open end (??) of the first quadrant. As it travels, its
speed increases. So this is really quite complicated motion, and very different from the first two examples.
| 
|
- The final example in this series is x(t)=cos(t), and
y(t)=cos(t). Again, the path traveled by the point is on the main
diagonal line y=x. But now the dynoamics are extremely
different. Because cosine oscillates endlessly between –1 and +1, the
motion of the point whose position is described by these equations is
on the line y=x and only between (–1,–1) and (1,1). It moves back and
forth between these points, completing a round trip in every time interval of length 2Pi. This is very different motion from the other examples.
| 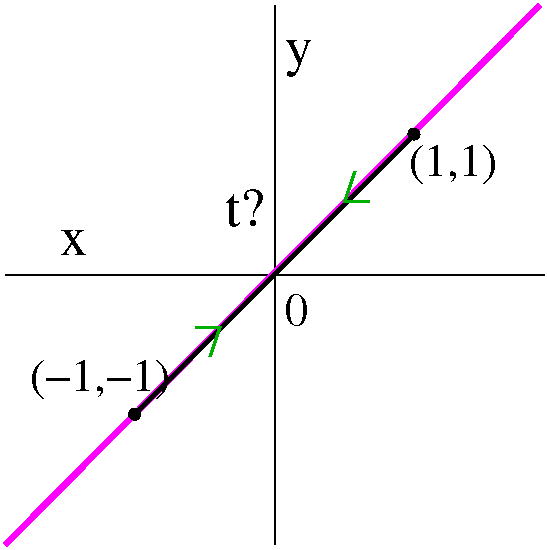
|
Example 3
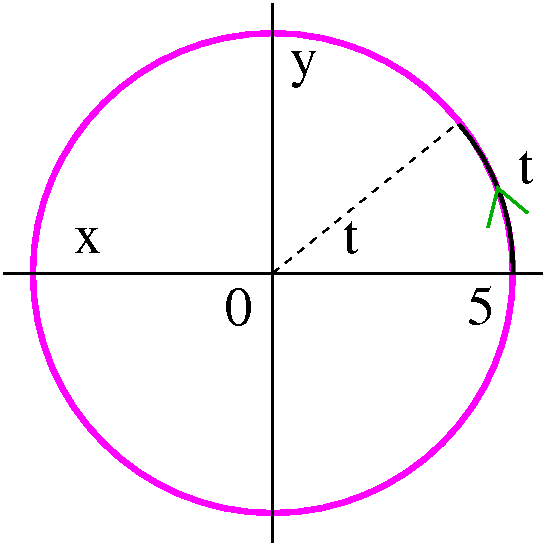
I considered x(t)=5cos(t)and y(t)=5sin(t). This is a slight
variant of the very first example. Since x(t)/5=cos(t) and
y(t)/5=sin(t), I "know" that the particle's path must be on
(x/5)2+(y/5)2=1, so
x2+y2=52, a circle whose center is
(0,0) and radius is 5.
The fact that the path lies on the circle whose equation is given is
fairly clear. But I was asked a slightly different question in class:
why does the point travel in a counterclockwise direction? When
you learn about velocity vectors, this may also be "fairly" clear, but
right now, if you plug in t=0, the point (x(t),y(t)) is (5,0), and if
you plug in π/2, the point is (0,5). Therefore I feel that travel
proceeds in a counterclockwise direction, from (5,0) to (0,5) and so
on.
|
|
What if x(t)=5cos(t) and y(t)=3sin(t)? Then the
trig identity gives (after elimination of the parameter)
(x/5)2+(y/3)2=1 as the possible path of the
point. This is an ellipse centered at (0,0). Its wider part (total
length 10) is on the horizontal axis, as shown. The vertical extant of
the ellipse is 6.
So I attempted to create a moving image of this curve. I hope it is
helpful to you. The parameterization is by central angle. Speed
varies. (I will discuss this next time.)
| 
|
A bug drawing out a thread ...
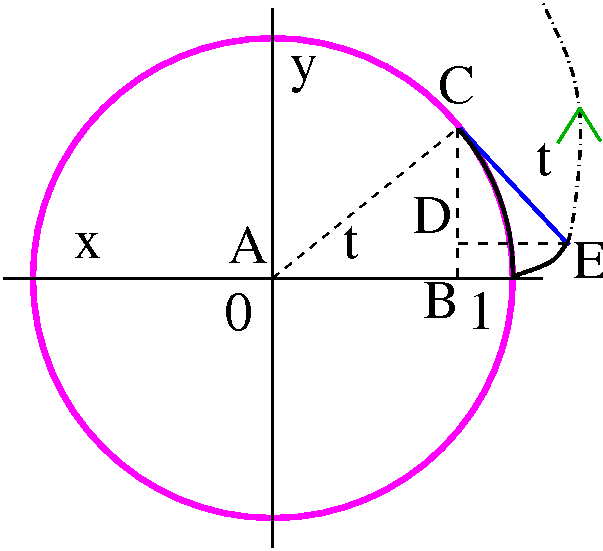 Thread is wound around the unit circle centered at the origin. A bug
starts at (1,0) and is attached to an end of the thread. The bug
attempts to "escape" from the circle. The bug moves at unit speed.
Thread is wound around the unit circle centered at the origin. A bug
starts at (1,0) and is attached to an end of the thread. The bug
attempts to "escape" from the circle. The bug moves at unit speed.
I would like to find an expression for the coordinates of the bug at
time t. Look at the diagram. The triangle ABC is a right triangle, and
the acute angle at the origin has radian measure t. The hypotenuse
has length 1, and therefore the "legs" are cos(t) (horizontal leg, AB)
and sin(t) (vertical leg, BC). Since the line segment CE is the bug
pulling away (!) from the circle, the line segment CE is tangent to
the circle at C. But lines tangent to a circle are perpendicular to
radial lines. So the angle ECA is a right angle. That means the angle
ECD also has radian measure t. But the hypoteneuse of the triangle ECD
has length t (yes, t appears as both angle measure and length
measure!) so that the length of DE is t sin(t) and the length of
CD is t cos(t).
The coordinates of E can be gotten from the coordinates of C and the
lengths of CD and DE. The x-coordinates add (look at the picture) and
the y-coordinates are subtracted (look at the picture). Therefore the
bug's path is given by x(t)=cos(t)+t sin(t) and
y(t)=sin(t)–t cos(t).
| t between 0 and 1 | t between 0 and 10
Note that the scale is changed! |
|---|
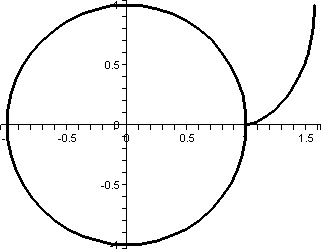 |
 |
Finally to the right is an animated picture of the bug moving. Maybe
you can understand this picture better: maybe (!!).
This curve is more typical of parametric curves. I don't know any easy
way to "eliminate" mention of the parameter. This seems to be an
authentically (!) complicated parametric curve, similar to many curves
which arise in physical and geometric problems. It has an official
name. It is called the evolute of the circle.
| 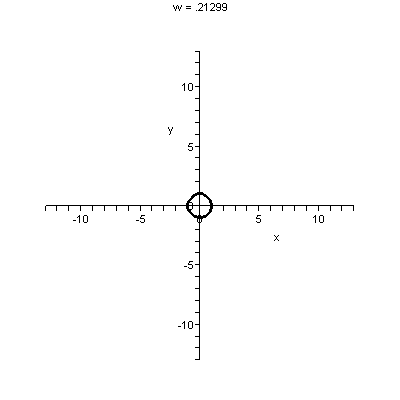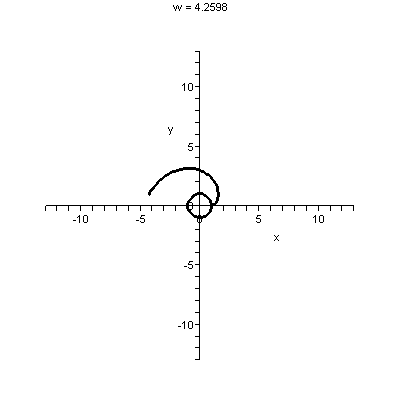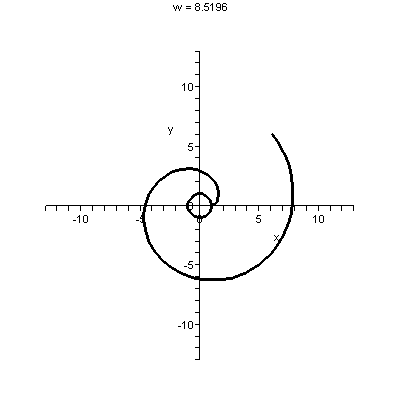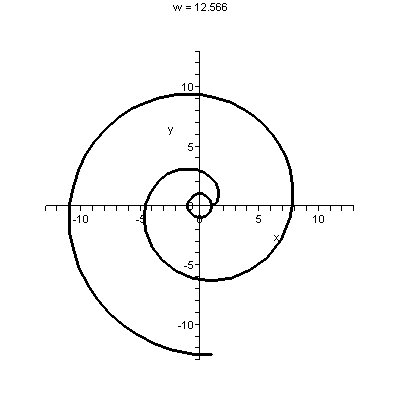
|
My favorite parametric curve
This is x(t)=1/(1+t2) and y(t)=t3–t. I
would like to analyze this curve a bit differently from the other
examples by separately considering the horizontal and vertical
components.
| The horizontal control |
|---|
|
Here we consider x as a function of t. The function has even degree
and is therefore symmetric: if (t,x) is on the curve, so it
(–t,x). Actually, the function is relatively simple. Consider positive
t. As t increases, x decreases, and since 1+t2→∞
x→0. So we get a picture as shown below.
Since this represents the horizontal part of the motion described by
this parametric curve, the result is this in the (x,y) plane: the
point for large negative t starts close to the x-axis. Then as t
increases, it slowly moves right. At its largest it is 1 unit to the
right of the vertical axis. Then it slowly moves back towards the
vertical axis again.

|
| The vertical control |
|---|
|
In this case, I'm considering the y-component of the moving point. I
could think of this as the vertical control of some sort of scanning
machine. The function has odd degree and is antisymmetric (if (t,y) is
on the curve, then (–t,–y) is on the curve). It is a cubic polynomial
with three real roots, at 1, –1, and 0. The graph is shown to the
right.
The curve in the (t,y) plane starts very low left, then up, then down,
then up, way way up on the right.
But this is a description of the vertical motion. Now what could we
"see" in the (x,y) plane? The point
starts way way down (this is large negative y!), moves up,
bounces down, and then finally moves way way up.
| 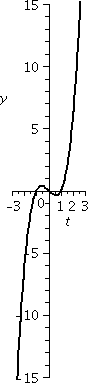 |
|
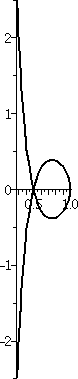 Combining these two motions can be difficult to do but with practice
you will find it easier. A part of the combined motion, the whole
parametric curve, is shown to the right. Indeed, it is a curve with a
self-intersection.
Combining these two motions can be difficult to do but with practice
you will find it easier. A part of the combined motion, the whole
parametric curve, is shown to the right. Indeed, it is a curve with a
self-intersection.
I don't know how to describe this curve accurately and efficiently
without the parametric "apparatus". The self-intersection occurs when
t=1 and t=–1 (that's where x=0 and y<1, as shown in the
picture). The point at which this occurs is (0,1/2).
|
Calculus?
Finally, very late in the lecture, I attempted some calculus. Here's
what I said.
Suppose we want to analyze what happens when the parameter changes
just a little bit, from t to t+Δt. Well, the point starts at
(f(t),g(t)). What can we say happens at
t+Δt? Well, f(t+Δt)≈f(t)+f´(t)Δt. Why is
this true? You can
think of this either 151 style as linear approximation, or from our
more sophisticated 152 approach, this is the constant and linear terms
in the Taylor series for f(t). Similarly for g(t) we know
g(t+Δt)≈g(t)+g´(t)Δt. Therefore the point in the
interval [t,t+Δt] moves from (f(t),g(t)) to
(approximately!)
(f(t)+f´(t)Δt,g(t)+g´(t)Δt). What is the slope of
the line segment connecting these points?
Slope
Take the difference in second coordinates divided by the difference in
the first coordinates. The result (there is a lot of cancellation) is
g´(t)/f´(t). If this were an xy curve, this would be noted
as dy/dx, the slope of the tangent line. In fact, people usually
remember the result in the following way:
dy dy/dt
-- = -----
dx dx/dt
and this can be used to get tangent lines (which I will do next time!).
Speed
Since Distance=Rate·Time, and in the time
interval [t,t+Δt] we move from (f(t),g(t)) to (approximately!)
(f(t)+f´(t)Δt,g(t)+g´(t)Δt), we can get the speed
(the Rate) by taking the distance between these points and dividing by
Δt. There is more cancellation here, and the result is
Speed=sqrt(f´(t)2+g´(t)2) or
___________
/(dx)2 (dy)2
Speed= / (--)+ (--)
/ (dt) (dt)
As you'll see if you take Math 251,
this is the sum of the squares of the
horizontal and vertical components of the velocity vector: it is,
in fact, the magnitude of the velocity vector.
Please: I will show you a few simple examples of this Wednesday, and
then go on to Polar Coordinates.
The second exam
was returned. More information is available.
| Wednesday,
April 22 | (Lecture #23) |
|---|
What do we know?
If a function f(x) has a power series expansion centered at a, then
f(x)=∑n=0∞[f(n)(a)/n!](x–a)n.
The partial sums of this series are Taylor polynomials, and this is
called a Taylor series.
Almost all the time we and other people in the world take a to be
0. Then the series is also called a Maclaurin series. Examples so far include:
- ex=1+x+{x2/2}+{x3/6+...=∑n=0∞[xn/n!] valid for all x.
- sin(x)=x–[x3/3!]+[x5/5!]–[x7/7!]+[x9/9!]...=∑n=0∞(–1)n+1x2n+2/(2n+1)! valid for all x.
- cos(x)=1–[x2/2!]+[x4/4!]–[x6/6!]+[x8/8!]–[x10/10!]...=∑n=0∞(–1)n+1x2n/(2n)! valid for all x.
We verified the convergence of the series to the indicated sums by
using the Error Bound for Taylor polynomials.
As I mentioned in class, I am not allowed to tell you
why these series resemble each other because your heads might
explode.
eix=cos(x)+isin(x)
The not-accidential resemblance will be discussed in your differential
equation course.
Book problem: 10.7, #21
Use multiplication to find the first four terms in the Maclaurin
series for exsin(x).
You may, if you wish, start finding derivatives, evaluating them at 0,
and plug into the formula
∑n=0∞[f(n)(0)/n!]xn. I
don't want to because I would prefer to be LAZY. If asked to contribute to the design of
a car, would you first invent the wheel? Well, maybe, if
you could really conceive of a better wheel. The idea is to
take advantage of what's already done. Please!
exsin(x)=(1+x+{x2/2}+{x3/6}+...)(x–[x3/3!]+[x5/5!]...)=
(multiplying by 1)(x–[x3/6]+[x5/120])+
(multiplying by x)(x2–[x4/6]+[x6/24])+
(multiplying by x2/2)([x3/2]–[x5/12]+[x7/48])+
(multiplying
by x3/6)([x4/6]–[x6/36]+[x8/144])+
(multiplying
by
x4/24)([x5/24]–[x7/stuff]+[x9/more stuff])+
Now I'll collect terms, going up by degrees:
x+x2–[x3/6]+[x3/2]–[x4/6]
+[x4/6]]+[x5/120]–[x5/12]+[x5/24]
Stop! since I only need the "bottom" 4 (in degree). I did go on, past the x4 terms, since I noticed they canceled. I interpreted the problem as asking for the first 4 non-zero terms.
The hard computation is
[x5/120]–[x5/12]+[x5/24]. But
1/120–1/12+1/24=1/120–10/120+5/120=–4/120=–1/30. My answer is therefore
x+x2+[x3/3]–[x5/30].
Book problem: 10.7, #14
Find the Maclaurin series of cos(sqrt(x)). Since
cos(x)=1–[x2/2!]+[x4/4!]–[x6/6!]+[x8/8!]–[x10/10!]...=∑n=0∞(–1)n+1x2n/(2n)! I know that
cos(sqrt(x))=1–[(sqrt(x))2/2!]+[(sqrt(x))4/4!]–[(sqrt(x))6/6!]+[(sqrt(x))8/8!]–[(sqrt(x))10/10!]...=∑n=0∞(–1)n+1(sqrt(x))2n/(2n)!
and so
cos(sqrt(x))=1–[x/2!]+[x2/4!]–[x3/6!]+[x4/8!]–[x5/10!]...=∑n=0∞(–1)n+1xn/(2n)!,
and please be LAZY.
Book problem: 10.7, #19
Find the Maclaurin series of (1–cos(x2)/x. Since
cos(x)=1–[x2/2!]+[x4/4!]–[x6/6!]+...
I know that
cos(x2)=1–[x4/2!]+[x8/4!]–[x12/6!]+...
and
1–cos(x2)=[x4/2!]–[x8/4!]+[x12/6!]+...
so that
(1–cos(x2)/x=[x3/2!]–[x7/4!]+[x11/6!]+...
|
An integral
The function e–x2 is extremely important in
probability. Its integral is called the error
function.
Suppose we want to compute
∫x=0.5e–x2dx. It can
be proved that e–x2 has no
antiderivative which can be written in terms in familiar
functions. How could we then compute this definite integral?
Its value, a pal of mine tells me, is approximately 0.46128. Well, I
could uses the Trapezoid Rule or Simpson's Rule or ... Look at this:
ex=∑n=0∞xn/n!
Substitute –x2 for x.
e–x2=∑n=0∞(–x2)n/n!=∑n=0∞(–1)nx2n)/n!
Integrate.
∫x=0x=.5e–x2dx=∫x=0x=.5∑n=0∞(–1)nx2n)/n! dx=∑n=0∞∫x=0x=.5(–1)nx2n)/n!=∑n=0∞(–1)nx2n+1/([2n+1]n!)|x=0x=.5
Evaluate.
The integral is∑n=0∞(–1)n(1/2)2n+1)/([2n+1]n!)
This series is alternating, and satisfies all the hypotheses of the
Alternating Series Test. Any partial sum is within the accuracy of the
first omitted term (the last workshop!). Well, if I want 5 digit
accuracy, I just need to find n so that
(1/2)2n+1)/([2n+1]n!) is less than .00001, which is
1/(100,000).
If n=4, then (1/2)9/[9·24] is {1/(512)}·[1/(216)]
which is 110,592. The sum from n=0 to 4, that is, S4, is
0.46128 (it is actually accurate one digit beyond that).
A familiar series
We know 1/(1–x). It is the sum of a geometric series with first term 1
and ratio equal to x. So
1/(1–x)=∑n=0∞xn. This
equation is valid when |x|<1, or –1<x<1. Some remarkable
things can be done with this series.
Logarithm
What the Maclaurin series of ln(x)? This is a trick question because
y=ln(x) looks like this  and the
limit of ln(x) as x→0+ is –∞ so ln(x)
can't have a Taylor series centered at 0. What's a good place
to consider? Since ln(1)=0, we could center the series at 1. Most
people would still like to compute near 0, though, so usually the
function is moved instead! That is, consider ln(1+x) whose graph now
behaves nicely at 0
and the
limit of ln(x) as x→0+ is –∞ so ln(x)
can't have a Taylor series centered at 0. What's a good place
to consider? Since ln(1)=0, we could center the series at 1. Most
people would still like to compute near 0, though, so usually the
function is moved instead! That is, consider ln(1+x) whose graph now
behaves nicely at 0  so we can
analyze it there.
so we can
analyze it there.
If f(x)=ln(1+x), I want to "find"
∑n=0&infin[f(n)(0)/n!]xn. Well,
f(0)=ln(1+0)=ln(1)=0, so we know the first term. Now
f´(x)=1/(1+x) so that ... wait, wait: remember to try to
be LAZY.
Look at
1
---
1+x
This sort of resembles the sum of a geometric series. We have two
"parameters" to play with, c, which is the first term, and r, which is
the ratio between successive terms. The sum is c/(1–r). If we take
c=1 and r=–x then 1/(1+x)=1/(1–{–x}) is the sum of a
geometric series. So
1/(1+x)=1–x+x2–x3+x4+...
Now let's integrate:
∫1/(1+x) dx=x–[x2/2]+[x3/3]–[x4/4]+[x5/5]+...+C
We need the "+C" because we don't officially know yet which
antiderivative we want to select to match up with ln(1+x). But just
test this at x=0. The function's value is ln(1)=0 and all of the
series terms are 0 except for the +C. So C must be 0.
ln(1+x)=x–[x2/2]+[x3/3]–[x4/4]+[x5/5]+...=&sumn=1∞[(–1)n+1xn/n]. This
is valid for |x|<1 certainly since that is the radius of
convergence of the geometric series we started with.
Computing with ln
What if x=–1/2 in the previous equation? Then ln(1–1/2)=ln(1/2)=–ln(2)
and this is approximately –69314. A friend of mine has just computed
&sumn=110[(–1)n+1(–.5)n/n]
and this turns out to be –.69306. We only get 3 decimal places of
accuracy. It turns out that this series converges relatively slowly
compared to the others we've already seen, which have the advantage of
factorials in the denominator. So this series is usually not directly
used for numerical computation, but other series related to it are used.
Book problem: 10.7, #9
Find the Maclaurin series of ln(1–x2).
Be LAZY. We know that
ln(1+x)=x–[x2/2]+[x3/3]–[x4/4]+[x5/5]+...=&sumn=1∞[(–1)n+1xn/n]. This
so we can substitute –x2 for x and get
ln(1–x2)=–x2–[(–x2)2/2]+[(–x2)3/3]–[(–x2)4/4]+[(–x2)5/5]+...=&sumn=1∞[(–1)n+1(–x2)n/n] and further
ln(1–x2)=–x2–[x4/2]–[x6/3]–[x8/4]–[x10/5]+...=–&sumn=1∞[(–1)n+1x2n/n] (valid for |x|<1).
Computing a value of a derivative
I know that the degree 8 term in the Maclaurin series for
ln(1–x2) is –[x8/4]. But it is also supposed to
be (by abstract "theory") [f(8)(0)/8!]x8. This means "clearly" (!!!) that
–1/4=[f(8)(0)/8!] and therefore f(8)(0)=–8!/4.
That's if you desperately wanted to know the value of the
derivative. An alternate strategy would be to compute the
8th derivative and evaluate it at x=0. Here is that
derivative: 6 8 4
10080 (28 x + x + 70 x + 28 x + 1)
- --------------------------------------
2 8
(-1 + x )
|
arctan
Let me try to find a Taylor series centered at 0 (a Maclaurin series)
for arctan. Well, the general Maclaurin series is
∑n=0∞[f(n)(0)/n!]xn
so we can just try to compute some derivatives and evaluate them at
0. Let's see:
n=0 f(x)=arctan(x) so f(0)=arctan(0)=0.
n=1 f´(x)=1/(1+x2) so
f´(0)=Stop this right now! Why?
Because this way is madness. Here is the 7th derivative of
arctan(x):
6 4 2
720 (7 x - 35 x + 21 x - 1)
------------------------------
2 7
(1 + x )
Does this look like something you want to compute?
Instead look at
1
----
1+x2
This sort of resembles the sum of a geometric series. We have two
"parameters" to play with, c, which is the first term, and r, which is
the ratio between successive terms. The sum is c/(1–r). If c=1
and r = –x2 then
1/(1+x2)=1/(1–{–x2}) is
the sum of a geometric series. So
1/(1+x2)=1–{x2}+{x2}2–{x2}3+{x2}4+...=1–x2+x4–x6+x8...
Now let's integrate:
∫1/(1+x2)dx=x–[x3/3]+[x5/5]–[x7/7]+[x9/9]...+C
The reason for the "+C" is that while we know that this series has
derivative equal to what we want, we don't know which specific
antiderivative will be arctan(x). This is really an initial value
problem and the +C represents the fact that we don't know the specific
solution. We need a value of arctan, and the simplest one is
arctan(0)=0. If we plug in x=0 to the series+C we get 0+C, so C should
be 0. And we have verified that (alternating signs, odd integer
powers, divided by odd integers [but not factorials!]):
- arctan(x)=x–[x3/3]+[x5/5]–[x7/7]+[x9/9]...=
∑n=0∞[(–1)2n+1x2n+1/(2n+1)]
Computing π
This series has been used to compute decimal approximations of
π. For example, if x=1, arctan(1)=π/4, so this must be
1–1/3+1/5–1/7+... but the series converges very slowly (for example,
the 1000th partial sum multiplied by 4 gives the
approximation 3.1406 for π which is not so good for all that
arithmetic!) . Here
is a history of some of the classical efforts to compute decimal
digits of π. You can search some of the known decimal digits of
π here. There are
more than a trillion (I think that is 1012) digits
of π's decimal expansion known. Onward! The methods used for such
computations are much more elaborate than what we have discussed.
|
In physics they say ...
Many of the force "laws" stated in physics are quadratic (second
degree) and therefore it is not surprising that squares and square
roots need to be computed frequently. What does sqrt(1+x) "look like"
near 0? Well, in this case I will try a direct computation. If
f(x)=sqrt(1+x) then ...
| Function | Value at x=0 |
|---|
| f(x)=(1+x)1/2 | 1 |
| f´(x)=(1/2)(1+x)–1/2 | 1/2 |
| f´´(x)=(1/2)(–1/2)(1+x)–3/2 | (1/2)(–1/2) |
| f(3)(x)=(1/2)(–1/2)(–3/2)(1+x)–5/2 | (1/2)(–1/2)(–3/2) |
I forget but
look at the pattern. | (1/2)(–1/2)(–3/2)(–5/2) |
So this Taylor series looks like
(1+x)1/2=1+(1/2)x+[(1/2)(–1/2)/2]x2+[(1/2)(–1/2)(–3/2)/6]x3+[(1/2)(–1/2)(–3/2)(–5/2)/24]x4+...
where those other strange numbers come from the factorials, of
course. Well, how might this be used in physics. Suppose you are
trying to analyze sqrt(1+w). If |w| is very small, well then I bet
that sqrt(1+w) is quite close top sqrt(1+0) which is 1. But the value
will not equal 1 if w is not 0. What sort of "first order" estimate
would I believe in? I bet that sqrt(1+w) is approximately 1+(1/2)w for
small w. I also believe that the error will be (roughly) proportional
to the size of w2 (that's the Error Bound again). For many
applications, knowing this is enough. But what if I wanted more
accuracy, and I wanted an estimate which was correct to "second order
terms". I bet this would take sqrt(1+w) and then the estimate woul dbe
1+(1/2)w–(1/8)w2, with an error which would be (roughly)
proportional to w3. Depending on the application you were
interested in, the estimate would be a bigger and bigger partial sum
of the Taylor series.
Why do I insist on writing the coefficients of the series in the silly
way done above? Why not just multiply out and write that? Well, if I
do the result may be rather deceptive. It would be
1+(1/2)w–[1/8]w2+[1/16]w3–[5/64]w4+...
so if I accidentally saw only the first 4 terms I might think there is
some obvious pattern to the series. Actually, the pattern is more
complicated, as the coefficient of w4 showns. There is an
abbreviation which is used (binomial coefficients) but the numbers are
complicated.
QotD
What are the terms up to order 10 (x10) in the Maclaurin
series for cos(5x3) (this is pretty close to a trick
question). The answer is short and easy, and lots of the terms
have their coefficient equal to 0.
An answer We know that
cos(x)=1–x2/2+x4/24+... and we should be
LAZY. So substitute
5x3 for x in that equation. This is substitution or
composition, it is not multiplication! For example, the
x2 term becomes (5x3)2 which is
25x6. In fact, we get
cos(5x3)=1–(25/2)x6+(625/24)x12/24+...
and the actual answer to this particular question is only the terms
1–(25/2)x6.
|
Here is what I was able to do last year, without the darn "blizzard"
causing a class to be canceled. Maybe you might find it helpful:
Binomial series with m=1/3
One of Newton's most acclaimed accomplishments was the description of
the Maclaurin series for (1+x)m. Here is more
information. In class and here, I'll specialize by analyzing what
happens when m=1/3. We'll use a direct approach by taking lots of
derivatives and trying to understand
∑n=0∞[f(n)(0)/n!]xn.
- n=0 f(x)=(1+x)1/3 so that f(0)=(1+0)1/3=1.
- n=1 f´(x)=(1/3)(1+x)–2/3 so that
f´(0)=(1/3)(1+0)–2/3=(1/3).
- n=2 f´´(x)=(1/3)(–2/3)(1+x)–5/3 so that
f´´(0)=(1/3)(–2/3)(1+0)–5/3=(1/3)(–2/3).
- n=3 f(3)(x)=(1/3)(–2/3)(–5/3)(1+x)–8/3 so that
f(3)(0)=(1/3)(–2/3)(–5/3)(1+0)–8/3=(1/3)(–2/3)(–5/3).
- n=3 f(4)(x)=(1/3)(–2/3)(–5/3)(–8/3)(1+x)–11/3 so that
f(4)(0)=(1/3)(–2/3)(–5/3)(–8/3)(1+0)–11/3=(1/3)(–2/3)(–5/3)(–8/3).
Maybe that's enough. I hope that you see the pattern. What do we get
for the beginning of the power series? We should not forget to divide
by the appropriate factorials.
1+(1/3)x+[(1/3)(–2/3)/2]x2+[(1/3)(–2/3)(–5/3)/2·3]x3+[(1/3)(–2/3)(–5/3)(–8/3)/2·3·4]x4+...
I'll come back to the general ideas later, but let's see how to use
this in various ways.
Naive numerical use
So you want to compute (1.05)1/3? This is a doubtful
assumption, and anyway wouldn't you do a few button pushes on a
calculator? But let's see:
Suppose we use the first two terms of the series and let x=.05:
(1+.05)1/3=1+(1/3)(.05)+Error
What's interesting to me is how big the Error is. Of course, we
have the Error Bound, which states that
|Error|≤[K/(n+1)!]|x–a|n+1. Here, since the top
term in the approximation is the linear term, we have n=1. And a, the
center of the series, is 0, and x, where we are approximating, is
.05. Fine, but the most complicated part still needs some work. K is
an overestimate of the absolute value of the second derivative of f on
the interval connecting 0 and .05. Well (look above!) we know that
f(2)(x)=(1/3)(–2/3)(1+x)–5/3. We strip away the
signs (not the sign in the exponent, since that means something
else!). We'd like some estimate of the size of (2/9)(1+x)–5/3
on [0,.05]. Well, it is exactly because of the minus sign in
the exponent that we decide the second derivative is decreasing
on the interval [0,.05] and therefore the largest value will be at the
left-hand endpoint, where x=0. So plug in 0 and get
1/9(1+0)–5/3=2/9. This is our K. So the Error Bound
gives us [(2/9)/2!](.05)2, which is about .00027. We have
three (and a half!) decimal digits of accuracy in the simple
1+(1/3)(.05) estimate.
What if we wanted to improve this estimate? Well, we can try another
term. By this I mean use 1+(1/3)(.05)+[(1/3)(–2/3)/2](.05)2 as
an estimate of (1.05)1/3. How good is this estimate? Again,
we use the Error Bound:
|Error|≤[K/(n+1)!]|x–a|n+1. Now n=2 and a=0 and
x=.05, and K comes from considering
f(3)(x)=(1/3)(–2/3)(–5/3)(1+x)–8/3. We need to
look at (10/27)(1+x)–8/3 on [0,.05]. The exponent is again
negative (what an accident not -- these methods are actually
used and things should be fairly simple!) and therefore the function
is again decreasing and an overestimate is gotten by looking at the
value when x=0, so (10/27)(1+x)–8/3 becomes
(10/27)(1+0)–8/3=(10/27). Hey,
[K/(n+1)!]|x–a|n+1 in turn becomes
[(10/27)/3!](.05)3, about .000008, even better.
Approximating a function on an interval
People usually use the partial sums considered above in a more
sophisticated way. For example, consider replacing (1+x)1/3
by
T2(x)=1+(1/3)x+[(1/3)(–2/3)/2!]x2=1+(x/3)–(x2/9)
anywhere on the interval [0,.05]. I like polynomials, because
they can be computed just by adding and multiplying. The function
(1+x)1/3 has this irritating and weird exponent, that I, at
least, can't readily estimate. What about the error? The Error
Bound declares that an overestimate of the error is
[K/3!]|x–0|3. Now if 0<x<.05, then the largest
x3 can be is (.05)3. What about K? Again, we
look at the third derivative with the signs (not the exponent
sign!) dropped. This is (10/27)(1+x)–8/3 which we are
supposed to estimate for any x in [0,.05]. But since the third
derivative is still decreasing (–1/3<0) again the K is gotten by
plugging in x=0. Hey: the estimate is the same as what we had before,
about .000008. Below are some pictures illustrating what's going on.
| (1+x)1/3 & T2(x) on [0,.05] |
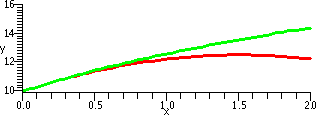
(1+x)1/3 & T2(x) on [0,2] |
|---|
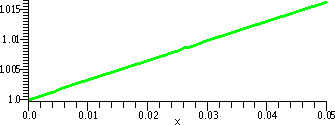 |
 |
Comments
Yes, there really really are two curves
here. One, (1+x)1/3, is green and one,
T2(x)=1+(x/3)–(x2/9), is red. But the pixels in
the image overlay each other a lot, because the error, .000008, makes
the graphs coincide on the [0,.05] interval. There are only a finite
number of positions which can be colored, after all!
| Comments
This graph perhaps shows more about what's going on. The domain
interval has been changed to [0,2]. The K in the Error Estimate
is not changed, but the x's now range up to 2. So [K/3!]x3
becomes as a worst case estimate [(10/27)/3!]23, which is
about .49. You can see T2(x) revealed (!) as just a
parabola opening downward (hey, 1+(x/3)–(x2/9) has
–1/9 as x2 coefficient!). The two curves are
close near x=0, and then begin to separate as x grows larger.
|
Improving the approximation
The whole idea is maybe by increasing the partial sum (going to
Tn(x)'s with higher n's) we will get better
approximations. This is only usable if the approximations are easy to
compute (nice polynomials with simple coefficients) and if the error
estimates are fairly easy to do. This actually occurs so that people
use these ideas every day.
Binomial series in general
Suppose m is any number (yes: any
number). Then
- (1+x)m=1+mx+[m(m–1)/1·2]x2+[m(m–1)(m–2)/1·2·3]x3+[m(m–1)(m–2)(m–3)/1·2·3·4]x4+...,
valid for |x|<1.
People who use this frequently have developed special notation for the
weird coefficients which occur. So
[m(m–1)(m–2)(m–3)/1·2·3·4] is abbreviated as 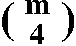 . These are called binomial
coefficients. . These are called binomial
coefficients.
|
The list ...
- ex=1+x+{x2/2}+{x3/6+...=∑n=0∞[xn/n!] valid for all x.
- sin(x)=x–[x3/3!]+[x5/5!]–[x7/7!]+[x9/9!]...=∑n=0∞(–1)n+1x2n+2/(2n+1)! valid for all x.
- cos(x)=1–[x2/2!]+[x4/4!]–[x6/6!]+[x8/8!]–[x10/10!]...=∑n=0∞(–1)n+1x2n/(2n)! valid for all x.
- 1/(1–x)=1+x+x2+x3+...=∑n=0∞xn
valid for |x|<1.
- ln(1+x)=x–[x2/2]+[x3/3]–[x4/4]+[x5/5]+...=∑n=1∞[(–1)n+1xn/n]
valid for |x|<1.
- arctan(x)=x–[x3/3]+[x5/5]–[x7/7]+[x9/9]...=
∑n=0∞[(–1)2n+1x2n+1/(2n+1)]
- (1+x)m=1+mx+[m(m–1)/1·2]x2+[m(m–1)(m–2)/1·2·3]x3+[m(m–1)(m–2)(m–3)/1·2·3·4]x4+...,
valid for |x|<1.
| Wednesday,
April 15 | (Lecture #22) |
|---|
There is a little bit more posted now about how to investigate the
workshop problem. Please look.
Power series ...
I recalled what had already been said about power series. Here we
go:
Definition
A power series centered at x0 (a fixed number) is an
infinite series of the form
∑n=0∞an(x-x0)n
where the x is a variable and the an are some collection of
coefficients. It resembles an infinite degree polynomial. Usually I
(and most people) take x0=0 because this just makes
thinking easier.
|
Calculus and power series
Hypothesis Suppose the power series
∑n=0∞an(x–x0)n
has some positive radius of convergence, R, and suppose that f(x) is
the sum of this series inside its radius of convergence.
Differentiation The series
∑n=0∞n(an)(x–x0)n–1
has radius of convergence R, and for the x's where that series
converges, the function f(x) can be differentiated,
and f´(x) is equal to the sum of that series.
Integration The series
∑n=0∞[an/(n+1)](x–x0)n+1
has radius of convergence R, and for the x's where that series
converges, the sum of that series is equal to an indefinite integral
of f(x), that is
∫f(x)dx.
|
Convergence and divergence
A power series centered at x0 always has an interval of
convergence with the center of that interval equal to
x0. Inside this interval of convergence, the series
converges absolutely and therefore converges. Outside the interval,
the series diverges. The power series may or may not converge on
the boundary of the interval. The interval may have any length between
0 and ∞. Half the length of the interval is called the radius of
convergence.
|
If a function has a power series then ...
Suppose I know that f(x) is equal to a sum like
A+B(x–x0)+C(x–x0)2+D(x–x0)3+E(x–x0)4+...
and I would like to understand how the coefficients A and B and C and
D etc. relate to f(x). Here is what we can do.
Step 0 Since
f(x)=A+B(x–x0)+C(x–x0)2+D(x–x0)3+E(x–x0)4+...
if we change x to x0 we get f(x0)=A. All the
other terms, which have powers of x–x0, are 0.
Step 1a Differentiate (or, as I said in class, d/dx) the
previous equation which has x's, not x0's. Then we have
f´(x)=0+B+2C(x–x0)1+3D(x–x0)2+4E(x–x0)3+...
Step 1b Plug in x0 for x and get
f´(x0)=B. All the
other terms, which have powers of x–x0, are 0.
Step 2a Differentiate (or, as I said in class, d/dx) the
previous equation which has x's, not x0's. Then we have
f´´(x)=0+0+2C+3·2D(x–x0)1+4·3E(x–x0)2+...
Step 2b Plug in x0 for x and get
f´´(x0)=2C, so
C=[1/2!]f(2)(x0). All the other terms,
which have powers of x–x0, are 0.
Step 3a Differentiate (or, as I said in class, d/dx) the
previous equation which has x's, not x0's. Then we have
f(3)(x)=0+0+0+3·2·1D+4·3·2E(x–x0)1+...
Step 3b Plug in x0 for x and get
f(3))(x0)=3·2·1D=3!C
so D=[1/3!]f(3)(x0). All the other terms,
which have powers of x–x0, are 0.
ETC. Continue as long as you like. What we
get is the following fact: if
f(x)=∑n=0∞an(x–x0)n
then an=[f(n)(x0)/n!]. This is
valid for all non-negative integers, n. Actually, this formula is one
of the reasons that 0! is 1 and the zeroth derivative of f is f
itself. With these understandings, the formula works for n=0.
What this means is
If a function is equal to a power series, that power series must
be the Taylor series of the function.
I hope you notice, please please please, that the partial sums of
the Taylor series are just the Taylor polynomials, which we studied earlier.
Usually I'll take x0=0, as I mentioned so that
(x-x0)n becomes just xn. Then the
textbook and some other sources call the series the Maclaurin
series but I am too lazy to remember another name. A useful
consequence of this result (it will seem sort of silly!) is that if a
function has a power series expansion, then it has exactly one power
series expansion (because any two such series expansions are both
equal to the Taylor series, so they must be equal). This means if we
can get a series expansion using any sort of tricks, then that series
expansion is the "correct one" -- there is only one series
expansion. I'll show you some tricks, but in this class I think I will
just try some standard examples which will work relatively easily.
ex
I'll take x0=0. Then all of the derivatives of
ex are ex, and the values of these at 0 are all
1. So the coefficients of the Taylor series, an, are
[f(n)(x0)/n!]=1/n!. The Taylor series for
ex is therefore
∑n=0∞[1/n!]xn.
e–.3
Let's consider the Taylor series for ex when
x=–.3. This is
∑n=0∞[1/n!](–.3)n. What
can I tell you about this? Well, for example, my "pal" could compute a
partial sum, say
∑n=010[1/n!](–.3)n. The
result is 0.7408182206. That's nice. But what else do we know? Well,
this partial sum is T10(–.3), the tenth Taylor
polynomial for ex centered at x0=0, and
evaluated at –.3. The Error Bound gives an estimation of
|T10(–.3)–e–.3|. This Error
Bound asserts that this difference is at most
[|K|–.3–0|11/11!], where K is some overestimate
of the 11th derivative of ex on the interval
between –.3 and 0. Well, that 11th derivative is also
ex. And we know that ex is increasing
(exponential growth after all!) so that for x's in the interval
[–.3,0], ex is at most e0=1, and we can
take that for K. So the Error Bound is
1|–.3–0|11/11!. Now let's look at some numbers:
|–.3|11=0.00000177147 and 11!=39,916,800, and their
quotient is about 4·10–14.
This means that e–.3 and T10(–.3) agree at least
to 13 decimal places. Indeed, to 10 decimal places, e–.3 is
reported as 0.7408182206, the same number we had before. Wow? Wow!
Let's change 10 to n and 11 to n+1. Then
|Tn(–.3)–e–.3| is bounded by
K|–.3–0|n+1/(n+1)!. Here K=1 again because all of the
derivatives are the same, ex. Since
1|–.3–0|n+1/(n+1)!→0 as n→∞ what do we
know?
I think that the sequence {Tn(–.3)} converges, and
its limit is e–.3. Since this sequence of Taylor polynomial
values is also the sequence of partial sums of the series
∑n=0∞[1/n!](–.3)n, I
think that the series converges, and its sum is
e–.3. Therefore
e–.3=∑n=0∞[1/n!](–.3)n.
e.7
We tried the same sequence of ideas with x=.7. We could first examine
T10(.7). This is
∑n=010[1/n!](.7)n. To 10
decimal places, this is 2.0137527069. We have information from the
Error Bound. It declares that |T10(.7)–e.7| is
no larger than K|.7–0|11/11!. Here K is an overestimate of
the 11th derivative, which is ex, on the
interval [0,.7]. The exponential function is (still!) increasing, so
the largest value is at x=.7. But I don't know e.7. I do
know it is less than e1 which I hardly know also. I will
guess that e<3. So a nice simple K to take is 3. Let me try
that. The Error Bound is less than 3|.7–0|11/11!. Let's do
the numbers here.
11!=39,916,800 (again) but .711=0.0197732674 (small, but
not as small as |–.3|11). The Error Bound
3|.7–0|11/11! is about 2·10–9, not quite
as small.
Now e.7, to 10 decimal places, is 2.0137527074 and this is
close enough to the sum value quoted before.
Again, go to n and n+1: |Tn(.7)–e.7| is less
than 3|.7–0|n+1/(n+1)!, and again, as n→∞ this
goes to 0. Our conclusion is:
The sequence {Tn(.7)} converges, and
its limit is e.7. Since this sequence of Taylor polynomial
values is also the sequence of partial sums of the series
∑n=0∞[1/n!](.7)n, I
think that the series converges, and its sum is
e.7. Therefore
e.7=∑n=0∞[1/n!](.7)n.
e50
Just one more example partly because we'll see some strange
numbers. Let's look at T10(50)
which is
∑n=010[1/n!]50n.
This turns out to be (approximately!) 33,442,143,496.7672, a big
number. The Error Bound says that |T10(50)–e50|
is less than K|50–0|11/11! where K is the largest
ex can be on [0,50]. That largest number is e50
because ex is increasing. I guess e50 is less
than, say, 350, which is about
7·1023. I'll take that for K. Now how big is that Error?
K|50–0|11/11! still has 11! underneath but now the top is
growing also. This is approximately 9·1034, a sort
of big number.
The situation for x=50 may look hopeless, but it isn't really. To
analyze |Tn(50)–e50| we need to look at
K[(50)n+1/(n+1)!]. Here the fraction has power growth on
the top and factorial growth on the bottom. Well, we considered this before. I called it a
"rather sophisticated example". Factorial growth is faster eventually
than power growth. So this sequence will →0 as
n→∞. A similar conclusion occurs:
e50=∑n=0∞[1/n!](50)n.
In fact, e50 is 5.18470552858707·1021
while the partial sum with n=100,
∑n=0100[1/n!](50)n has value
5.18470552777323·1021: the agreement is not too bad,
relatively.
And generally for exp ...
It turns out that
∑n=0∞[1/n!]xn converges
for all x and its sum is always ex. The way
to verify this is what we just discussed. Most actual computation of
values of the exponential function relies on partial sums of this
series. There are lots of computational tricks to speed things up,
but the heart of the matter is the Taylor series for the exponential
function.
Sine
We analyzed sine's Taylor polynomials, taking advantage of the cyclic
(repetitive) nature of the derivatives of cosine:
sine→cosine→-sine→-cosine then back to sine. At
x0=0, this gets us a cycle of numbers:
0→1→0→-1→0 etc. The Taylor series for sine
centered at 0 leads off like this:
x–[x3/3!]+[x5/5!]–[x7/7!]+[x9/9!]–...
It alternates in sign, it has only terms of odd degree, and each term
has the reciprocal of an "appropriate" factorial (same as the degree)
as the size of its coefficient. Using summation notation, which is
convenient and compact, this series is
∑n=0∞[(-1)n/(2n+1)!]x2n+1.
What happens to the error bound?
This is similar to what we did with exp. There are two claims: the
series
∑n=0∞[(-1)n/(2n+1)!]x2n+1
converges and the sum of the series is sin(x). Well, to see that this
is true we investigate the difference between sin(x) and
SN, the Nth partial sum of the series. But
SN is the same as TN(x), the Nth
Taylor polynomial. And the error bound tells us that
|sin(x)-TN(x)|≤[K/(N+1)!]|x-0|n+1. Just as
before, [|x|N+1/(N+1)!]→0 as N→∞. What about
the K's? If they misbehave (get very big) that could make the whole
estimate lousy. But in fact in this specific case, |K| is an
overestimate on the size of some derivative of sine. But all of the
derivatives of sine are +/-sine and +/-cosine, and these all are ≤1
in their absolute values. So, in fact, we're done. We have verified
that the series converges and that sin(x) is its sum.
Cosine
We could duplicate this work for cosine, or, as I mentioned in class,
be a bit cleverer. Since we know that
sin(x)=∑n=0∞[(-1)n/(2n+1)!]x2n+1
(valid for all x) we could differentiate this equation. The result is
cos(x)=∑n=0∞[(-1)n/(2n+1)!](2n+1)x2n.
In fact, most people realize that (2n+1)/(2n+1)! is 1/(2n)! so that we
have verified the equation
cos(x)=∑n=0∞[(-1)n/(2n)!]x2n
for all x.
A numerical example: cos(1/3)
How close is
1–[(1/3)2/2!]+[(1/3)4/4!]–[(1/3)6/6!]+[(1/3)8/8!]–[(1/3)10/10!]
to cos(1/3)? Here we sort of have two candidates because
T10(1/3) is the same as T11(1/3) since the
11th degree term is 0.
Error bound, n=10 So we have K|(1/3)–0|11/11!, where
K is a bound on the size of the 11th derivative of
cosine. Hey: I don't care much in this example, because I know that
this derivative is +/–cosine or +/–sine, so that I can take K to be
1. Now it turns out that (1/3)11/11! is about
1.4·10–14. This is tiny, but ...
Error bound, n=11 This is even better. So we have K|(1/3)–0|12/12!, where
K can again be taken as 1 (this is easier than exp!)
So (1/3)12/12! is about
4·10–15, even tinier.
Hey, cos(1/3)=0.944956946314738 and
T10(1/3)=0.944956946314734.
Cosine and sine estimates
For both cosine and sine, the estimates are easy because K for both
can be taken to be 1.
Is success guaranteed?
The material in this lecture showed that exp and sine and cosine have
Taylor series and their Taylor series converge everywhere and the sum
of each Taylor series is always equal to the original function. This
is a wonderful situation, and, for example, is essentially used to
compute values of exp and sine and cosine using partial sums of the
series (as I wrote above, there are some other "computational tricks
to speed things up, but the heart of the matter is the Taylor
series").
But these are the first and nicest and simplest examples. The
situation is not always so easy. We will see a few functions where
things don't work out. I can even think about one of them with you
now. Consider tangent. Certainly if we take x0 to be 0, we
can differentiate tangent lots of times and "get" a Taylor series for
tangent centered at 0. The reason I wrote "get" with quotes is that
the coefficients of the Taylor series for tangent are well-known in
the math world to be rather, well, rather irritating and difficult to
predict and understand. So already there's a problem. How about
convergence? Things also don't go well there because, if you remember
tangent's graph, vertical asymptotes occur at odd multiples of
Π/2. You can't expect that the series will converge, for example,
at +/-Π/2 and, in fact, the radius of convergence turns out to be
only Π/2 (this is not so obvious, actually). Most calculators I know
compute values of tangent by computing values of sine and cosine and
then dividing. This is easier than direct computation of tangent.
|
Maintained by
greenfie@math.rutgers.edu and last modified 4/16/2009.


 The rectangular graph of 1+sine, shown here, decreases
down to 0 and then increases to +1. The polar graph dips to 0 and then
goes back up to 1. The dip to 0 in polar form is geometrically a sharp
point! I used "!" here because I don't believe this behavior is easily
anticipated. The technical name for the behavior when r=3Π/2 is
cusp.
The rectangular graph of 1+sine, shown here, decreases
down to 0 and then increases to +1. The polar graph dips to 0 and then
goes back up to 1. The dip to 0 in polar form is geometrically a sharp
point! I used "!" here because I don't believe this behavior is easily
anticipated. The technical name for the behavior when r=3Π/2 is
cusp.

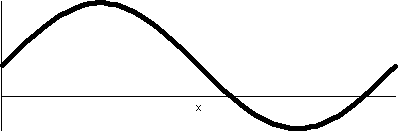 The rectangular graph on the interval [0,2Π] of sine moved up by 1/2
shows that this function is 0 at two values, and is negative between
two values. The values are where 1/2+sin(θ)=0 or sin(θ)=–1/2. The values of θ satisfying that equation in the
interval of interest are Π+Π/6 and 2Π–Π/6. The curves goes down to
0 distance from the origin at Π+Π/6, and then r is negative until
2Π–Π/6. The natural continuation of the curve does allow negative
r's, and the curve moves "behind" the pole, making a little loop
inside the big loop. Finally, at 2Π–Π/6, the values of r become
positive, and the curve links up to the start of the big loop.
The rectangular graph on the interval [0,2Π] of sine moved up by 1/2
shows that this function is 0 at two values, and is negative between
two values. The values are where 1/2+sin(θ)=0 or sin(θ)=–1/2. The values of θ satisfying that equation in the
interval of interest are Π+Π/6 and 2Π–Π/6. The curves goes down to
0 distance from the origin at Π+Π/6, and then r is negative until
2Π–Π/6. The natural continuation of the curve does allow negative
r's, and the curve moves "behind" the pole, making a little loop
inside the big loop. Finally, at 2Π–Π/6, the values of r become
positive, and the curve links up to the start of the big loop.


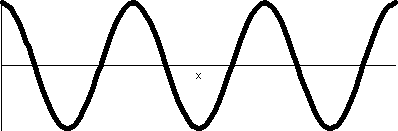 The rectangular graph, shown here, has three pairs of ups
and downs. The polar trace covers the leaves twice. The six
up-and-downs of cos(3θ) (magically?) reduce to retracings of
half of the loops. I hope I made this evident. I
introduced some deliberate distortion in the second
tracing. (!) Without the distortion, the second tracing
could not be seen at all. The imaginary "point" travels over the
computer screen's pixels and colors them (from white to black in this
case). The second trip could not be noticed since the pixels had
already been flipped to black. So I put in a small perturbation so
that the second layer of travel could be seen.
The rectangular graph, shown here, has three pairs of ups
and downs. The polar trace covers the leaves twice. The six
up-and-downs of cos(3θ) (magically?) reduce to retracings of
half of the loops. I hope I made this evident. I
introduced some deliberate distortion in the second
tracing. (!) Without the distortion, the second tracing
could not be seen at all. The imaginary "point" travels over the
computer screen's pixels and colors them (from white to black in this
case). The second trip could not be noticed since the pixels had
already been flipped to black. So I put in a small perturbation so
that the second layer of travel could be seen.
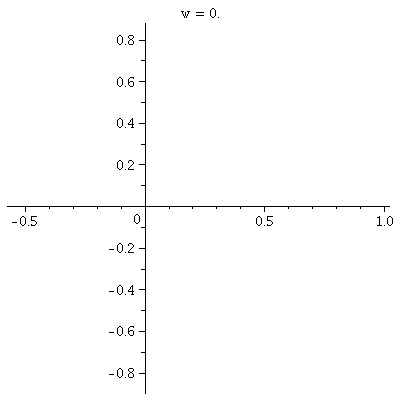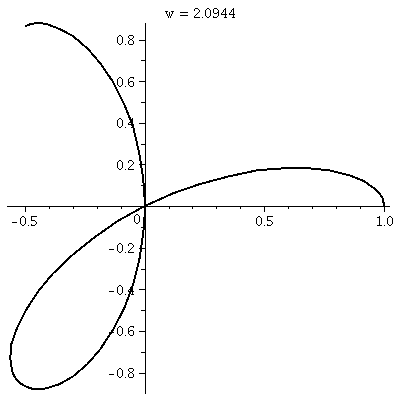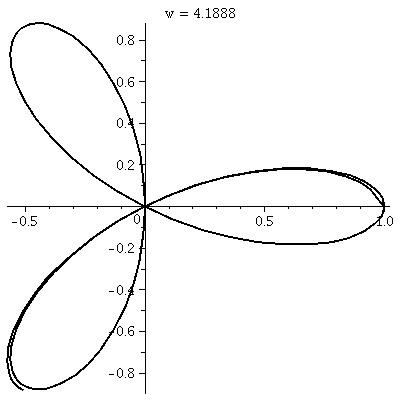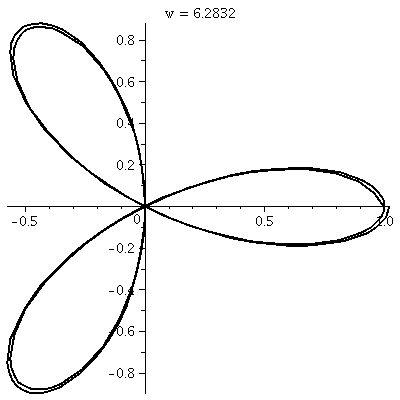
 The rectangular
graph. to the right, shows four bumps up and four bumps down. There
are no retracings of already colored points, so that the wiggles up
and down of cos(4θ) all result in 8 leaves.
The rectangular
graph. to the right, shows four bumps up and four bumps down. There
are no retracings of already colored points, so that the wiggles up
and down of cos(4θ) all result in 8 leaves.
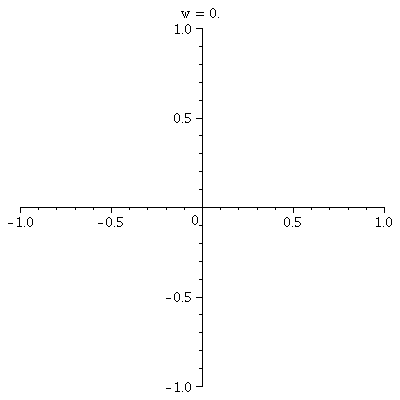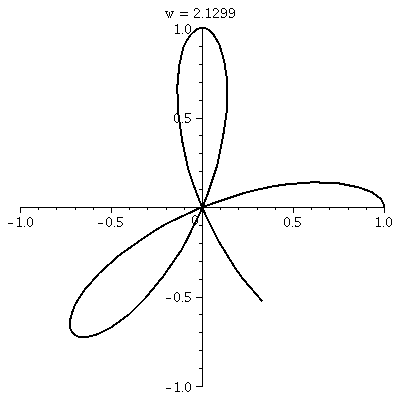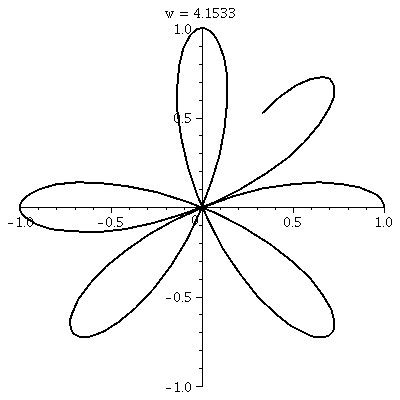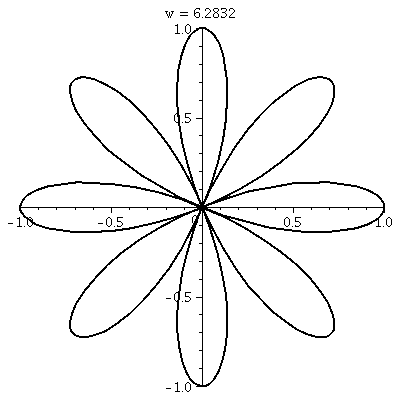
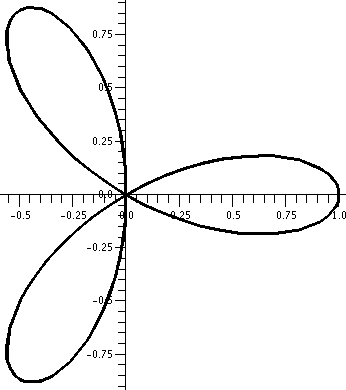


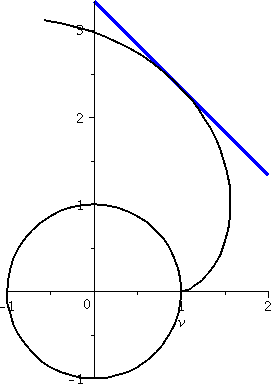
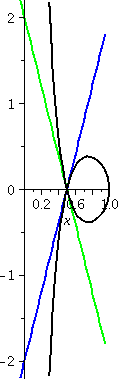 Tangent lines
Tangent lines Now this does resemble what I know about the motion of a planet in
orbit. When it is far away from the center of the orbit, the planet
will have large potential energy and relatively small kinetic energy
(it will move slowly). This is near t=0 and t=Π. When it is close
to the center of the orbit, the planet moves faster, and the kinetic
energy is larger, while the potential energy, measured by the work
needed to move closer/farther from the center, decreases.
Now this does resemble what I know about the motion of a planet in
orbit. When it is far away from the center of the orbit, the planet
will have large potential energy and relatively small kinetic energy
(it will move slowly). This is near t=0 and t=Π. When it is close
to the center of the orbit, the planet moves faster, and the kinetic
energy is larger, while the potential energy, measured by the work
needed to move closer/farther from the center, decreases.
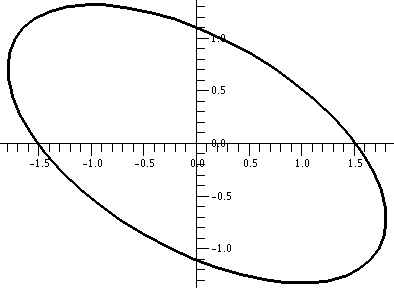



 The idea of polar coordinates
The idea of polar coordinates
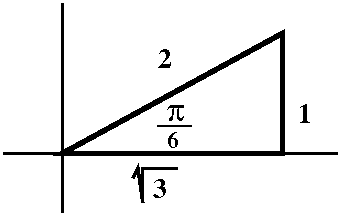
 If you consider the picture to the right, I hope that you can fairly
easily "read off" how to go from r and θ to x and y:
If you consider the picture to the right, I hope that you can fairly
easily "read off" how to go from r and θ to x and y:



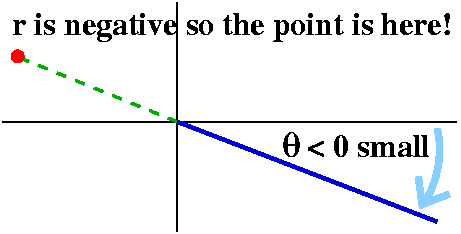
 Example 1
Example 1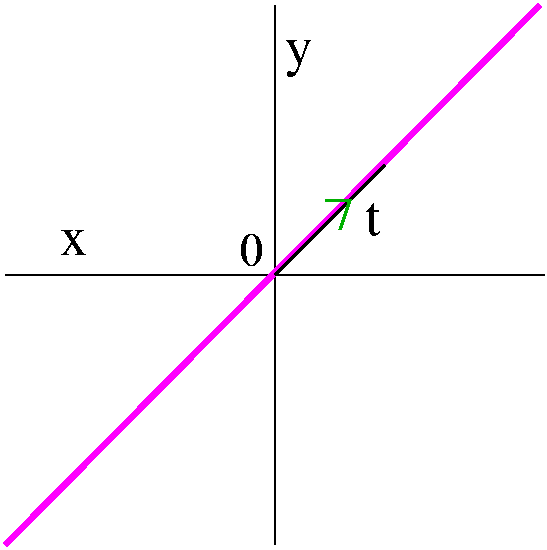


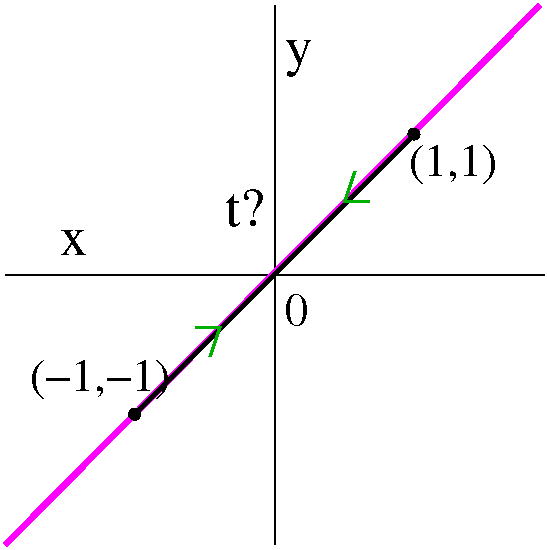


 Thread is wound around the unit circle centered at the origin. A bug
starts at (1,0) and is attached to an end of the thread. The bug
attempts to "escape" from the circle. The bug moves at unit speed.
Thread is wound around the unit circle centered at the origin. A bug
starts at (1,0) and is attached to an end of the thread. The bug
attempts to "escape" from the circle. The bug moves at unit speed.

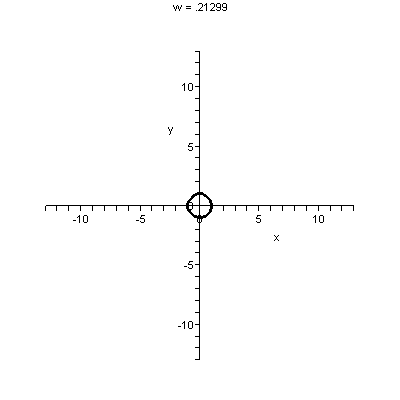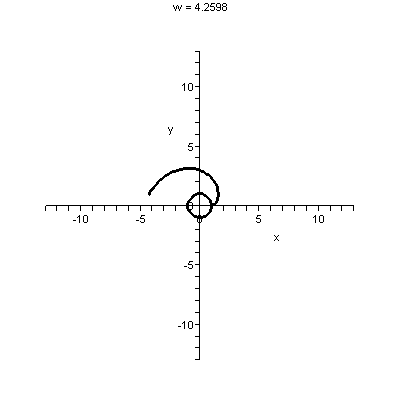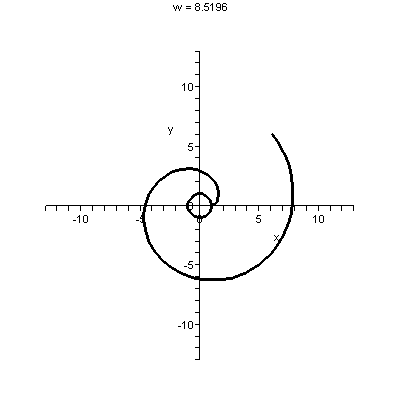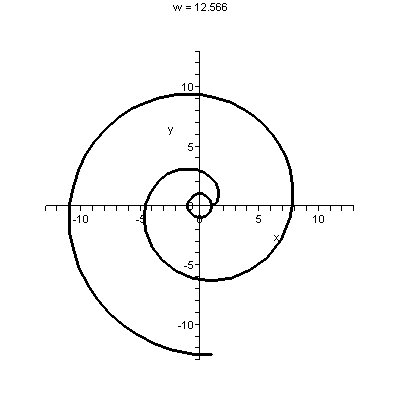

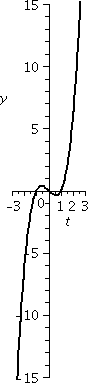
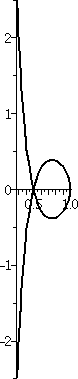 Combining these two motions can be difficult to do but with practice
you will find it easier. A part of the combined motion, the whole
parametric curve, is shown to the right. Indeed, it is a curve with a
self-intersection.
Combining these two motions can be difficult to do but with practice
you will find it easier. A part of the combined motion, the whole
parametric curve, is shown to the right. Indeed, it is a curve with a
self-intersection.

