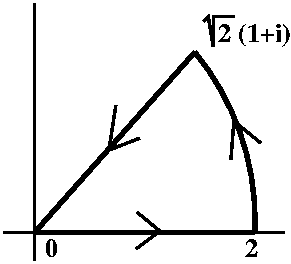Later material
| Special Edition,
celebrating the 14th lecture |
|---|
| an opportunity to "inform" the
students |
 To the right is a picture of a male domestic turkey. It has wattles
("a loose fleshy appendage on the head or throat of a turkey or other
birds.") which are sort of enlarged jowls ("the external loose skin on
the throat or neck when prominent."). Certainly the instructor does not look
like a turkey. Domestic turkeys are supposed to be extremely
stupid. Wild turkeys, which are much thinner and mostly brown, are
quite shy and difficult to observe. They do exist on Busch Campus! Try
to find one. (Don't get caught in the Rhus toxicodendron while
seeking the Meleagris gallopavo, please.)
To the right is a picture of a male domestic turkey. It has wattles
("a loose fleshy appendage on the head or throat of a turkey or other
birds.") which are sort of enlarged jowls ("the external loose skin on
the throat or neck when prominent."). Certainly the instructor does not look
like a turkey. Domestic turkeys are supposed to be extremely
stupid. Wild turkeys, which are much thinner and mostly brown, are
quite shy and difficult to observe. They do exist on Busch Campus! Try
to find one. (Don't get caught in the Rhus toxicodendron while
seeking the Meleagris gallopavo, please.)
Compact ... closed ... bounded ...
The definition
Suppose (X,d) is a metric space, and K is a compact subset of
X. "Compact" means that if K is contained in a union of open sets,
then it must be contained in a union of finitely many of these sets
("Every open cover has a finite subcover").
Compact implies closed
Suppose p is in X and p is a limit of a sequence of points
{kj} where each of the kj's is in K. Consider
the open set Un={x in X with d(x,p)>1/n}. Certainly
Un is open and Un+1 contains Un. If p
is not in K, then {Un} is an open cover of K, so
some finite subcollection of them covers K also. Since the
Un's are nested, then is one UN which contains
K. But if p is a limit of points in K, we have a contradiction: some
of the kj's satisfy d(p,kj)<1/N. Therefore p
must be in K. We have proved that if K is compact, then K is closed in
X.
Compact implies bounded
Suppose K is compact. Consider any point p, and look at
Un={x in X with d(x,p)<n}. Of course Un is
contained in Un+1. Certainly the union of the
Un's contains K (it is all of X!). So (because of finite
subcover and the nesting) there is N with K contained in
UN. This means (triangle inequality) that the distance
between any two points of K is less than 2N. We have proved that if K
is compact, then K is bounded in X.
Extra credit
Which of those proofs is Artinian? Which is Noetherian?
Heine-Borel
The
Heine-Borel Theorem declares that if S is a subset of
Rn which is closed and bounded, then S is compact. This is
not true in all metric spaces.
Example 0
If (X,d) is a metric space, then (X,d/(1+d)) is a metric space with
the same topology. In this metric, however, X is bounded. Since X is
also closed as a subset of itself, X is closed and bounded. If
you believe the converse of "compact implies closed and bounded" you
would need to believe that every metric space is compact.
O.k.: this example is silly.
Example 1
Consider the unit disc in R2 (or C!). This is our X, and d
will be the usual metric. Look at the subset S of X which is those
complex numbers with |z|<1 and Im(z)=0 (the x-axis inside the unit
disc). S is not compact. The open cover whose elements are
D1-(1/n)(0) (here n is a positive integer) does not have a
finite subcover. But S is bounded (hey: the bound is 2, but that's
o.k., X is bounded also). And S is a closed subset of X (look at X\S,
which is nice and open). |  |
Example 2
Suppose X=C([0,1]), the collection of continuous functions on the unit
interval. The distance on X will be the sup norm. That is, if f and g
are in X, d(f,g)=supt in [0,1]|f(t)-g(t)|. Since
f and g are continuous, the sup is actually achieved: it is a max.
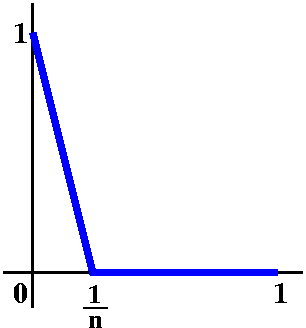
Suppose S is the collection of functions whose distance from the 0
function is at most 1. So S={f in C([0,1]) with |f(t)|<=1}. This is
the closed unit ball and is certainly closed and bounded. Now look at the functions fn defined piecewise by:
fn(x)=0 if x>1/n; fn(x)=1-nx if x is in [0,1/n].
A picture of a typical fn is shown to the right. Certainly
fn is continuous and is in S.
|  |
|
Notice, please, that if x is
in [0,1], the function EVx defined by
EVx(f)=f(x) (evaluation at x) is continuous on C([0,1])
(evaluation at a point is less than the max of the function!). Suppose
the sequence {fn} converges in X. Since
EVx(fn)-->0 if x>0 and
EV0(fn)=1, the limit would have the value 1 at 0
and be 0 for x>0. This is not a continuous function, so
{fn} does not converge in X. Now you use these
fn's to create an open cover of S which does not have a
finite subcover (this isn't too hard, I think). S is closed and
bounded, but not compact.
|
Of course we are really using here is that C([0,1]) is not locally
compact. But that's not very strange. Combinatorists: contemplate a
graph with infinite degree at a vertex. If the edges are each like an
interval, then that graph will not be locally compact in any natural
topology.
What really goes wrong with the example above is that the fn functions wiggle too
much. We will return to consider the issue of wiggling
later ("equicontinuity").
Here's another example ...
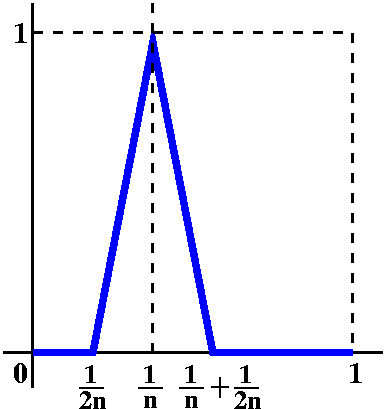 This example is maybe a bit more irritating. Define gn by
the following piecewise recipe (really the picture to the right is
what I'm thinking of and I only hope that what follows is
almost correct):
This example is maybe a bit more irritating. Define gn by
the following piecewise recipe (really the picture to the right is
what I'm thinking of and I only hope that what follows is
almost correct):
gn(x)=0 if x<1/{2n} or if
x>{1/n}+1/{2n};
gn(x)=(n+n2)x-(n+1)/2 for x in
[1/{2n},1/n];
gn(x)=-(n+n2)x-(something) for
x in [1/n,(1/n)+(1/{2n})].
Now define hn=g(2n) (that's
2n in the subscript for the g's). The bumps for the
hn's don't "interfere" with each other. Then:
- Each hn is in S, the closed unit ball of
X=C([0,1]).
- The distance between hn and hm is 2 if n and
m are not equal. They can't converge. This may be very disconcerting
to you if you don't believe in "infinite dimensions".
- Make an open cover of S which doesn't have a finite subcover using
these functions: take a ball of radius 1 around each hn,
and then "throw in" X\{all of the hn's} (the last set is
open because the set of hn's is discrete in X).
Is this better? These functions wiggle a great
deal, also.
| Friday,
October 20 | (Lecture #14) |
|---|
Here is the last appearance of the algebra table.
Mr. Williams and others interacted with
the lecturer for this presentation. A key obervation is identifying
the units (the invertible elements for multiplication) in the
ring of convergent power series. These turn out to be exactly those
power series with non-zero constant term. Then ideals etc. can be
studied easily.
The lecturer mentioned that the following observations are now almost
easy, but proving them from the definitions would be somewhat
irritating.
- The inverse of a convergent power series with non-zero
constant term is a convergent power series (such a series has sum
which is holomorphic, the reciprocal of a non-zero holomorphic
function is holomorphic, and that function then is representated by a
convergent power series).
- The Cauchy product of convergent power series is a convergent
power series (I guess I could do this from the definition, but it
still would not be pleasant -- I would prefer to "sidestep" through -->
-- holomorphicity).
- The composition of two convergent power series is
convergent. Again using the same type of approach as in the previous
paragraph yields the result easily. A more direct approach may get
involved (for example, combinatorialists should know a bit about
Faà
di Bruno's formula.
Maximum Modulus Theorem (version 2)
Maximum principle (for harmonic functions)
"Proof"
What! No harmonic conjugate!!
Minimum principle (for harmonic functions)
Hot plates
Uniqueness for the Dirichlet Problem
The lecturer mentioned the distinction between "compact" and "closed
and bounded" which is discussed further in the special edition above.
The set Kt mentioned in the homework is compact in C for
any compact K and non-negative real t, since the mapping
Kx[0,t]-->C given by (k,s)-->k+s is continuous and
the domain is compact.
We estimated f´ from f using the Cauchy Integral Formula for
derivaitives (the same can be done for f(n) by either using
the appropriate Cauchy Integral Formula or by "interpolating" more
compact sets to get higher derivatives).
The instructor asked if students really believed the result, since,
say, sin(nx) on [0,1] is bounded in absolute value by 1 but its
derivative wiggles a great deal. How can we "reconcile" this? Of
course, the answer is that [0,1] in C is very "thin" and a compact
neighborhood of it must stick out into the top and bottom
halfplanes. There sin(nz) has exponential behavior in both real and
imaginary parts, so sin(nz) gets enormous on any such set.
We stated and verified the famous Weierstrass result: if
{fn} is a sequence of holomorphic functions which converge
uniformly on compact subsets of an open set U, then so do the sequence
of derivatives, {fn´}. Therefore the u.c.c. limit of
such functions is itself holomorphic, and, in fact, all derivatives
converge to the appropriate derivative of the limit.
This means that "construction" of a holomorphic function can be much
easier in some technical sense than, say, construction of a
C function was for Borel's Theorem.
function was for Borel's Theorem.
Let RN be the Nth roots of unity, and let
NRN be that set multiplied by N. If R is the union of
NRN for N>1, we "constructed" an explicit function which
was holomorphic on all of C\R. This was very easy using the
Weierstrass Theorem.
| Tuesday,
October 16 | (Lecture #13) |
|---|
Notes by Hanna Komlos, edited, with
some comments, by the instructor.

Mr. Williams suggested a few entries in
the algebra table.
We began by recalling a theorem from last time with a picture in mind.
Theorem If f is holomorphic in an open connected set U, and if
f=0 (f equals the zero function!) in some
disc contained in U  , then f=0 in U
, then f=0 in U  .
.
Corollary If f and g are holomorphic in U, and if f=g on some
disc contained in U, then f=g on U.
This leads to some questions about the zeros of a holomorphic
function: how "often" can a holomorphic function be equal to 0?
First, an entire function is one that is holomorphic on the
whole complex plane. For any function f, we define Z(f) to be the set
of zeros of f.
- Question Is there an entire function f with Z(f)=the empty
set?
Answer Sure, take f(z)=ez.
- Question Is there an entire f with #Z(f)=1? (Here "#S" is the
cardinality of a set S.)
Answer Take f(z)=z.
- Question Is there an entire f with #Z(f)=2?
Answer Take f(z)=z(z-1). And in general, taking
f(z)=(z-1)(z-2)···(z-n) will give an entire f
with #Z(f)=n.
- Question Is there and entire f with #Z(f)=
 ?
?
Answer Well, f(z)=0. But if we add that f is NOT the zero
function, then we can take f(z)=z(ez-1), since
Z(f)={2n(Pi)i | n is an integer}.
- Question Is there an f holomorphic in D1(0) with
#Z(f)=
 ?
?
Answer Take f(z)=e(i/(1-z)). Then for z=1-1/(2nPi),
z is in the disc and f(z)=0.
- Question How about Z(f) uncountable? (With f still not the
zero function.)
Answer No! C is sigma compact. This means it is the union of
countably many compact subsets. We verify this for C by writing C as
the union over all positive integers n of the closure of
Dn(0)(the disc of radius n centered at 0). If Z(f) is
uncountable then there exists an n>0 so that the numbers of elements
of Z(f) in the closure of Dn(0)is infinite (if this is
finite for all n then the zero set is the countable union of finite
sets and hence countable). Since the closure of Dn(0) is
compact, there exists a z* in Dn(0) which is a
limit point of Z(f). Then zj-->z* for some
distinct zj in the closure of Dn(o), and
f(z*)=0 since f is continuous. For all e>0, the
intersection of De(z*) and Z(f) is infinite. But
our local description of f then shows (since f is not N to one for any
N) that f must be constnat.
So we can replace the disc hypothesis with the hypothesis that
Z(f) has an accumulation point in U in the first theorem and
corollary. !!!! excitement!
Basically, if two holomorphic functions agree on a set with an
accumulation point in their common (connected) domain then they are
equal.
For instance, there is exactly one entire function f such that
f(x)=sin(x) for all x in R. More generally, any definition of a
holomorphic function which agrees with something on R works.
We also get some nice properties for free. For example, since sin(z)
and cos(z) are entire, so are (sin(z))2 and
(cos(z))2, so since (sin(x))2+(cos(x))2=1
in R, (sinz)2+(cosz)2=1 in C. Similarly,
sin(A+B)=sin(A)cos(B)+cos(A)sin(B) on all of C follows from the equality
of the two functions in R.
Then sin(z)=sin(x+iy)=sin(x)cos(iy)+sin(iy)cos(x). But we already know
the Taylor series for cosine on R which must be the power series for
cosine on C: cos(iy)= n=0
n=0 [(-1)n(iy)2n]/(2n)!=
[(-1)n(iy)2n]/(2n)!= n=0
n=0 y2nn/(2n)!=cosh(y)
and similarly sin(iy)=i sinh(y).
y2nn/(2n)!=cosh(y)
and similarly sin(iy)=i sinh(y).
So sin(x+iy)=sin(x)cosh(y)+i sinh(y)cos(x).
What is Z(sine)? Since cosh is never 0, sin(x+iy)=0 implies sin(x)=0,
so x=nPi. Then cos(x) is nonzero, so sinh(y)=0, which implies y=0.
Thus Z(sine)={nPi | n is an integer}. All of the zeros of
the entire function sine are the same as the real zeros of the
"calculus function" sine.
Here is a Rutgers qualifying exam problem: Suppose f is holomorphic on
a neighborhood of zero, and you know for all integers k that
f(1/k)=100i/k4. What is f?
Answer The sequence {1/k}k=1 has
an accumulation point in any neighborhood of zero, so since f(z) and
100iz4 (A guess! A guess, only!)
agree on {1/k}k=1
has
an accumulation point in any neighborhood of zero, so since f(z) and
100iz4 (A guess! A guess, only!)
agree on {1/k}k=1 , f(z) must actually be
100iz4.
, f(z) must actually be
100iz4.
Philosophy: this sort of says that if a sequential
statement can be proved about a holomorphic function (say, for
example, by some inductive proof, and if the
statement is true on a set with an accumulation point, it is
always true. This is almost startling.
So any
algebra or simple calculus property which is true on a set with an
accumulation point must be true on the whole (connected) open
set.
Now we consider the "other case" from last time. If a holomorphic
function f is not locally constant, then for all p in U there is a
natural number N so that f(z)=a+(k(z))N where k is
holomorphic in some disc of radius e centered at p, k(p)=0 and
k´(p)=0.
Notice that in this description, f is a composition of open
mappings. These are functions so that the image of any open set is
open.
 Question Can such a function be a folding of the complex plane?
Question Can such a function be a folding of the complex plane?
Answer No, we can't have a holomorphic function which folds C
since we can't fit an open set around any image point on the
crease. (It is also true that the number of inverse image points
around one of the "crease" points varies from 2 to 1 to 0, and this is
also impossible.
Open Mapping Theorem Suppose U is an open connected set, and f
is a non-constant holomorphic function on U. Then f is an open mapping.
"Proof" We just need to show that open neighborhoods of points
in the domain have images which are open. But if f is non-constant,
its local description is always like that above, for some
positive integer N. The local description takes open sets to open
sets, so f is open.
 A Calc 3 exam problem Let S=[0,2pi]x[0,2pi], a subset of
R2. What's the maximum value of
f(x,y)=sqrt[(sinx)2(cosh)2+(cosx)2(sinhy)2]
on S?
A Calc 3 exam problem Let S=[0,2pi]x[0,2pi], a subset of
R2. What's the maximum value of
f(x,y)=sqrt[(sinx)2(cosh)2+(cosx)2(sinhy)2]
on S?
Answer In Calc 3, we would begin by searching for interior
critical points. But since we recognize f as |sinz|, there can be no
such points. Why? If q were such a point, then f(q)>=f(z) for nearby
z. But then sine would map the region near q to those w's with
|w|<=q. And f(q) would be on the boundary of
D|f(q)|(0). The points near q would be mapped inside the
closure of the disc, and certainly an open neighborhood of q would not
be mapped by sine to an open neighborhood of sin(q), which is a
contradiction to the Open Mapping Theorem. The max must occur
on the boundary (and where is that max? Can you find
it?)
Maximum Modulus Theorem (version 0) If f is holomorphic in an open
and connectioned set U and f is not constant, then g(z)=|f(z)| has no
local maximum.
Remark We can't change "max" to "min". For instance, consider
f(z)=z on D1(0).
Maximum Modulus Theorem (version 1) Suppose U is open and connected,
and U closure is compact in C. Suppose f is continuous on U closure
and holomorphic on U. Then supz in U closure|f(z)| exists
and equals supz on  U|f(z)|.
U|f(z)|.
Proof |f| attains a maximum since it is continuous on a compact
set. One inequality comes for free since  U is contained in the
closure of U. If f is a constant function, then both sides are the
same. By version 0, when f is not constant, the max on U closure
cannot be in U, so it is on the boundary.
U is contained in the
closure of U. If f is a constant function, then both sides are the
same. By version 0, when f is not constant, the max on U closure
cannot be in U, so it is on the boundary.
Some computer-drawn pictures
Since we have powerful graphics programs, we should be able to "see"
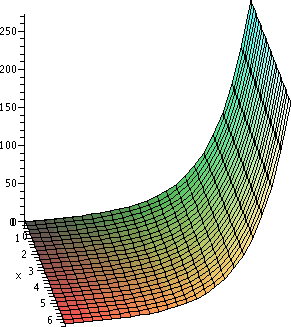
some of these results. Below are two pictures produced by Maple. The picture to the left is the image of
|sin(x+i y)| on the rectangle [0,2Pi]x[0,2Pi]. I looked at it and
was a bit confused. Certainly what's shown does not seem to have an
interior maximum, so that was o.k. But I wanted to see some boundary
variation, especially along the boundary part with Im(z)=0. I didn't
"see" it. Then I realized: consider the vertical scale. The picture
automatically adjusts things (this is Scaling
Constrained, the default) so that the image fills the
viewing window. The imaginary part involves cosh and sinh. These are
basically exponentials, so they grow enormously. For example, the
approximate value of |sin(2Pi+2Pi i)| is 267.75. I can't expect
to "see" wiggles of 0 to 1 on the border if the vertical scale is
several hundred times as high. The exponential growth will be used
more in the next lecture. The picture to the right is made with an
idea that is not new, but is rather convenient in situations where
there's lots of data, and the data may vary in size a great
deal. Consider arctan (the usual real calculus function arctan). It is
strictly increasing, has domain all of R, and has range
(-Pi/2,Pi/2). If we compose data whose size is "unknown" with arctan,
then we'll get output which preserves order, but which is restricted
in size. (Indeed, this feature is built into Maple itself if you ask for plotting of a function
from 0 to  , say.) So the picture on the right is
arctan(|sin(x+i y)|). Now I can "see" the result of
|sin(x)|2 when y=0. Since arctan preserves order, there is
still no interior local maximum. But there is a penalty (think about
this!) in the following: the convexity changes in the y-direction. The
left picture has x=constant sections of the graph appearing
(correctly) concave up, while the right picture has such sections
concave down. Is this correct? (Yes. Why?)
, say.) So the picture on the right is
arctan(|sin(x+i y)|). Now I can "see" the result of
|sin(x)|2 when y=0. Since arctan preserves order, there is
still no interior local maximum. But there is a penalty (think about
this!) in the following: the convexity changes in the y-direction. The
left picture has x=constant sections of the graph appearing
(correctly) concave up, while the right picture has such sections
concave down. Is this correct? (Yes. Why?)
 |
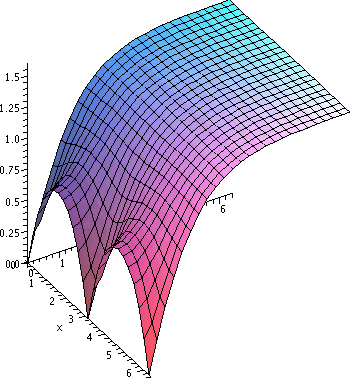 |
| |sin(x+i y)| | arctan(|sin(x+i y)|) |
|---|
| Friday,
October 12 | (Lecture #12) |
|---|
Notes by Vidit Nanda, edited, with
some comments, by the instructor.
During the course of previous lectures, we have encountered the
following commutative rings denoted by:
C[z], C{z}, and C[[z]]
which respectively represent the polynomials, convergent power series
and formal series in one variable with complex coefficients.
Followers of abstract algebra will be quick to remark that there are
ring monomorphisms
going from left to right, embedding one ring into the next.
The instructor attempted to fill the
empty boxes in the following table with "yes" or "no":
Using sophisticated monte-carlo
techniques, the instructor has filled out the first column and
requested algebraically inclined students to complete the remainder.
We really should know the answers!
We now move on to Goursat's Theorem, which the instructor claimed was
remarkable since it made no assumptions regarding the continuity of
the derivative, hence "nice to know", but lacking in any practical
value whatsoever. (The scribe would be remiss if he failed to point
out Avital Oliver's impassioned support of Goursat and the subsequent
seal of kosher approval shaped like the Star of David.)
Goursat's Theorem Suppose U is an open subset of C. If for any
given function f:U-->C, the limit defining f´(z) exists for all z in U,
then f is holomorphic on U.
Proof (A version of the proof that was provided in class is
also available in all its glory at
planetmath)
By our version of Morera's Theorem,
it suffices to prove that the integral of f around any rectangle in U
is zero. For contradiction, assume there is a rectangle R so that

 Rf(z)dz=A, where A is a nonzero complex number. Then,
we subdivide this rectangle into 4 smaller rectangles
R1,...,R4 so that
Rf(z)dz=A, where A is a nonzero complex number. Then,
we subdivide this rectangle into 4 smaller rectangles
R1,...,R4 so that
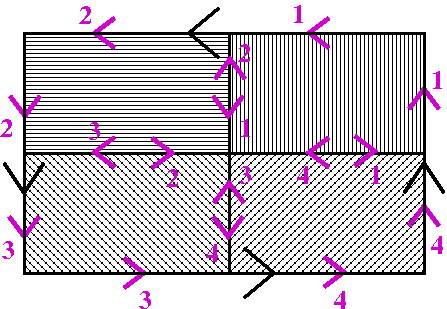
 j=14(
j=14(
 Rjf(z)dz)=A.
Rjf(z)dz)=A.
This is because the integrals along the "inner edges" cancel. The picture shown is an effort to persuade you that this
is correct. The labels are the directions on each boundary segment of
the borders of the inner rectangles.
Now, we claim that there is at least one j in {1,...,4} so that
|
 Rj(f dz)|>= |A|/4.
Rj(f dz)|>= |A|/4.
since otherwise the sum of all 4 integrals would have absolute
value strictly less than |A|, thus leading to contradiction. We can
now reapply our subdivision idea to this  Rj. Repeating this
process ad infinitum and relabelling the indices allows us to create a
strictly decreasing sequence of nested rectangles {Rp,p
in N} so that
Rj. Repeating this
process ad infinitum and relabelling the indices allows us to create a
strictly decreasing sequence of nested rectangles {Rp,p
in N} so that
|
 Rpf(z)dz|<= A|/4p. (Call this (i))
Rpf(z)dz|<= A|/4p. (Call this (i))
Now we observe that the intersection of all elements of {Rp}
must be a unique point by the nested set property,
What is this property?
In the following, assume that [Sj}j in N is a
nested sequence of subsets of R2. Here
nested means Sj+1 is a subset of Sj for
all j>=1.
- Find an example in R2 of a sequence so that the intersection is empty.
- Find an example in R2 of a sequence whose
diameters-->0 so that the intersection is empty.
- Find an example in R2 of a sequence of open sets so
that the intersection is empty.
Example (for all three)
Sj=(0,1/j)x(0,1/j) in R2, n in N.
Certainly diam(Sj)=sqrt(2)/j-->0 as n--> . .
- Find an example in R2 of a sequence of closed sets
{Sj} so that the intersection is empty.
Example
Sj=[j, ) (each is a subset of R1 and
hence a subset of R2). ) (each is a subset of R1 and
hence a subset of R2).
- What is the precise statement of the "nested set property"?
What is a (possibly approximate) proof?
|
so there is a unique
z* sitting in the intersection of all our rectangles. By hypothesis, we
know f´(z*) exists, so for every h in U, we have
f(z*+h)=f(z*)+hf´(z*)+o(|h|)
The first two terms on the right constitute a linear function on U, which
is clearly holomorphic, so by Cauchy's theorem the integral of the first
two terms around any rectangle in U is zero. So, define
g(z)=f(z)-f(z*)-(z-z*)f´(z*),
and note that if S in U is a rectangle, then

 Sf(z)dz=
Sf(z)dz=
 Sg(z)dz, (call this (ii))
Sg(z)dz, (call this (ii))
Now, since g is continuous by and the boundary  Rp of Rp is
compact for all p, we can set Mp to be the maximum value of
g(z) on
Rp of Rp is
compact for all p, we can set Mp to be the maximum value of
g(z) on  Rp; if
Lp is the length of
Rp; if
Lp is the length of  Rp, we can use the ML estimate to get
Rp, we can use the ML estimate to get
|
 Rpg(z)dz|<=MpLp (call this (iii))
Rpg(z)dz|<=MpLp (call this (iii))
But Lp=L/2p, where L= R1, and, since
g(z)=o(|z-z*|), we know that
Mp<=(Qp)2-p. Further,
Qp-->0 because of the little o part of the
differentiation definition. We can now combine (i), (ii) and (iii) and
get:
R1, and, since
g(z)=o(|z-z*|), we know that
Mp<=(Qp)2-p. Further,
Qp-->0 because of the little o part of the
differentiation definition. We can now combine (i), (ii) and (iii) and
get:
|A|/4p<=|  Sf(z)dz|<=(Qp)2-pL/2p
Sf(z)dz|<=(Qp)2-pL/2p
Which provides the desired contradiction, since the right side goes to
zero faster than the left side for nonzero A. QED
The Goursat Theorem has a proof which is rarely used in other
contexts. Let's move on to a point of view and some results which are
exploited in many ways. We want to get quite precise local
description of f.
Getting a precise local picture of holomorphic functions
Suppose f is holomorphic in some open set containing 0. Then we know
that there is R>0 and a sequence of complex numbers
{an}n=0 so that
f(z)=
so that
f(z)= n=0
n=0 anzn
for all z with |z|<R. Two alternatives occur:
anzn
for all z with |z|<R. Two alternatives occur:
- f is constant in the disc of radius R centered at 0
So all of the an's with n>0 are 0.
-
f is not constant in the disc of radius R centered at 0
There is a positive integer N with aN not 0 and
aj=0 for 1<=j<N.
Let's consider the second alternative, since the mapping properties of
f in that case may not be clear. We now know:
f(z)= n=0
n=0 anzn=a0+
anzn=a0+ n=N
n=N anzn=a0+zN
anzn=a0+zN n=N
n=N anzn-N.
anzn-N.
Of course, since the original series converges for |z|<R, the
series  n=N
n=N anzn-N
converges for |z|<R. But the sum of such a series, we now know,
represents a holomorphic function (let's call it g(z)) in that
disc. And we further know that g(0)=aN is not
zero. Since holomorphic functions are continuous, there is some
smaller disc of radius S, let us say, where g(z) is not 0 for all z
with |z|<S. But non-zero holomorhic functions in simply connected
open sets (suchn as discs!) have logs and roots of all orders. Thus
there is h, holomorphic in the disc of radius S centered at 0, so that
(h(z))N=g(z) for
all z with |z|<S.
anzn-N
converges for |z|<R. But the sum of such a series, we now know,
represents a holomorphic function (let's call it g(z)) in that
disc. And we further know that g(0)=aN is not
zero. Since holomorphic functions are continuous, there is some
smaller disc of radius S, let us say, where g(z) is not 0 for all z
with |z|<S. But non-zero holomorhic functions in simply connected
open sets (suchn as discs!) have logs and roots of all orders. Thus
there is h, holomorphic in the disc of radius S centered at 0, so that
(h(z))N=g(z) for
all z with |z|<S.
f(z)=a0+zNg(z)=a0+zNh(z)(h(z))N=a0+(zh(z))N.
Define the holomorphic function k by k(z)=zh(z). Then k(0)=0 and, by
the Product Rule, k´(0)=aN, which is not 0.
The easy case
Again we might possibly need to decrease S to some positive number
T. But, using the Inverse Function Theorem of "Calculus" in
R2 (a rather profound theorem!) we can state that k, in the
disc of radius T, is a diffeomorphism. That is, k restricted to
DT<0> is a bijection from that disc to an open neighborhood
of 0, and both k and its inverse are differentiable. But we know from
the homework assignment what the derivative of k is: a directly
conformal linear mapping, whose inverse is also directly conformal
(this is a linear algebra description of the Cauchy-Riemann equations).
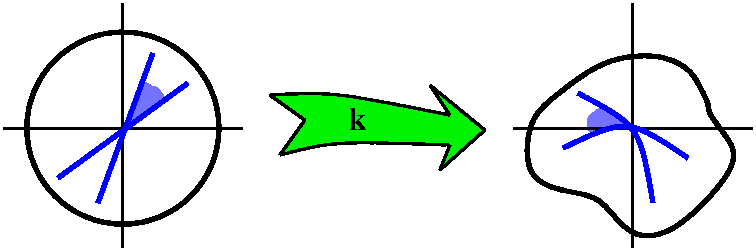 Smooth curves through a point z in the domain with some positive angle
are transformed into smooth curves with the same angle through the
corresponding image point, k(z). The curves are rotated by
arg(k´(z)). The local speed along the curves is multiplied
by |k´(z)|. There's just this one rotation and one magnification
factor, so locally the picture is easy (!?) to understand.
Smooth curves through a point z in the domain with some positive angle
are transformed into smooth curves with the same angle through the
corresponding image point, k(z). The curves are rotated by
arg(k´(z)). The local speed along the curves is multiplied
by |k´(z)|. There's just this one rotation and one magnification
factor, so locally the picture is easy (!?) to understand.
Power mappings near 0
Let's explore the mapping P defined by z-->zN for
N>1. For N=1, this is covered by the previous paragraph. In a disc
of radius T centered at 0, P is "fine" (locally) away from 0, since
then P´(z)=NzN-1 is not 0. But considered in all of
DT(0), P is N-to-1 except for 0. The inverse of a non-zero
w is given explicitly by b(w1/N) where w1/N is
one Nth root of w (if w=reiq then one value of
w1/N is r1/Nei/N) and where b is any of
the N Nth roots of 1. Remember that the Nth
roots of 1 form the vertices of an inscribed regular polygon with one
vertex at 0. P's mapping on DT(0) is an example of what is
called a branched covering map.
Covering maps
f:X-->Y is a covering map if for all y in Y, there is a
neighborhood Ny of y so that f-1(Ny)
is a disjoint union of neighborhoods Nx for each x in
f-1(y) so that f|Nx is a homeomorphism from
Nx to Ny. Examples of covering maps relevant to
this course are z-->zN on C\{0} (an N-to-1 mapping) and
z-->ez on C (an infinite-to-1 mapping).
It is not
necessarily true that all preimages of a point have the same
cardinality. For example, consider z-->z2 on those z's
satisfying 1<|z|<2 with arg(z) between 0 and, say, 3Pi/2. The
cardinality of the preimages will be either 1 or 2.
Branching/ramification
People say that the mapping P(z)=zN ramifies or
branches at 0. It is no longer a covering map. The inverse
images stick together (?) and become one point. But, except for that
failure, P is very nice. The average number (?!) of inverse images is
N (well, except for 0, this number is n), and this number is
called the degree or the order or the
multiplicity ... there are several names. The instructor
declared, "This number is used more or less in every area of math I
know about."
| To the right is a diagram which may
help you understand the mapping P. This is "specialized" to the case
N=3. The topologists tell us that one way to try to comprehend the
mapping is to imagine that it is the composition of two mappings. One
is "cubing", whose domain is a disc centered at the origin. The range
of this mapping, which is 1-1, is a weird topological space. Think of
it as D0 and D1 and D2, with an
interesting equivalent relation. Here is the equivalence relation: all
of the 0's in the discs are equivalent. If (z)j represents
the copy of z (for z in the disc) in Dj, then this means
that (0)0=(0)1=(0)2 (so all of the
origins are the "same" point). What about the other points? Let's pick
some random number in [0,2Pi], say v. Then for r>0, I will describe
a neighborhoon of (reiv)0: take the z's in an
ordinary neighborhood of reiv. If z=aeib, and
b>=v, then (z)0 is in the neighborhood of
(reiv)0. If z=aeib, and
b<v, then (z)2 is in the neighborhood of
(reiv)0. Also,
(reiv)0=(reiv)2. There is
a similar identification with radial edges of the other discs.
|
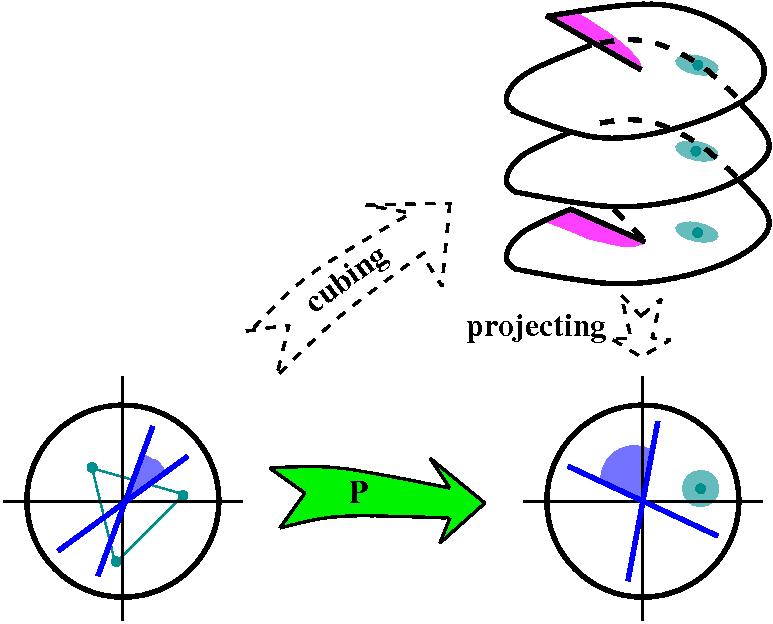 |
|
What I am attempting to describe is in the complicated picture
displayed. The
solid black borders of the magenta (?) regions should be
"identified". This identification space cannot be constructed in
R3 without self-intersection, and what is drawn is a
possible representation of it in R3. The mapping which is
called "cubing" sends z in the disc to w=z3 in the quotient
space, with the specific (w) depending upon whether z is
in the first third of the disc (arguments between 0 and 2Pi/3, then
j=0) or in the second third of the disc (arguments between 2Pi/3 and
4Pi/3, then j=1) or in the third third of the disc (arguments between
4Pi/3 and 2Pi, then j=2). Writing this is incredibly irritating and
hard to understand, so no wonder topologists never really prove
[The instructor's legal counsel has redacted the remainder of this
sentence.].
Finally, the projecting map just takes (w)j to w. The image
of two lines going through the origin becomes two lines going through
the origin but the angles involved are multiplied by 3. The inverse
image of a point away from the origin is, first, in the covering
space, three points. A neighborhood's inverse image is three blobs
over the neighborhood. Finally, back in the original disc, the inverse
image of a point which is not the origin is three points
forming in this case an equilateral triangle (N=3) which has 0 as its
center. Wow! The "cubing" part is 1-1, and the "projecting" part is 3-1.
The blue lines are just drawn in the domain
and range. The cyan points and region are
drawn pulling back from the range, into the covering space (for the
blob and point) and just the points, together with a possibly useful
triangle, in the domain.
|
The complete local description for non-constant holomorphic
functions
So if a holomorphic f is not locally constant, then f must be written
as a composition of the mappings z-->k(z) (a [directly] conformal
diffeomorphism) and P, which maps z to zN, an N-to-1 map
away from 0, which is conformal except at 0, and which, at 0,
multiplies the angle between curves by N, and, finally, the
translation,
z-->a0+z. Whew! Well, that is a rather neat qualitative
description.
Back to the constant case
Let us "exploit" the first alternative in the local description. What
should the "degree" be when f is just a constant term in some power
series expansion? People vary with what they say. Sometimes it is
asserted this should be 0, and sometimes it is asserted that it should
be  . Oh well. But being constant spreads throughout a
connected open set.
. Oh well. But being constant spreads throughout a
connected open set.
Theorem Suppose U is a connected open set, and suppose that
f is holomorphic in U. If there is p in U with the power series
expansion of f at p just equal to a constant term, then f is a
constant function. Indeed, all of the power series expansions of f
are just the constant term.
Proof If n is a positive integer, let Cn be the
collection of z's in U with f(n)(z)=0. Notice that since f
is holomorphic, f must be C , so f(n) is
continuous and Cn is a closed set. p is in Cn
for all n. Define C to be the intersection of all of the
Cn's. The intersection of closed sets is closed, and p is
in the intersection. So C is a closed non-empty subset of U. Take q
in C. For all positive integer n, f(n)(c)=0. But this means
that the power series expansion centered at q has only the zeroth
order term possibly non-vanishing (we last time identified the power
series centered at q as the Taylor series centered at q). And the
power series centered at q has a non-zero radius of convergence (at
least the distance from q to the boundary of U). So C contains a disc
of that radius centered at p. And C is therefore open. Since U is
connected, C=U. Since now f´(z)=0 in U, f is constant on U.
, so f(n) is
continuous and Cn is a closed set. p is in Cn
for all n. Define C to be the intersection of all of the
Cn's. The intersection of closed sets is closed, and p is
in the intersection. So C is a closed non-empty subset of U. Take q
in C. For all positive integer n, f(n)(c)=0. But this means
that the power series expansion centered at q has only the zeroth
order term possibly non-vanishing (we last time identified the power
series centered at q as the Taylor series centered at q). And the
power series centered at q has a non-zero radius of convergence (at
least the distance from q to the boundary of U). So C contains a disc
of that radius centered at p. And C is therefore open. Since U is
connected, C=U. Since now f´(z)=0 in U, f is constant on U.
We will show some of the ways this is used next time.
| Tuesday,
October 9 | (Lecture #11) |
|---|
Notes by Yunpeng Wang, edited, with
some comments, by the instructor.
Pictures???
Please note that I did draw pictures for each of the proofs given. But
for the three major results (the results that I threatened to make
into axioms if I couldn't prove them) I drew (what I consider to be)
exactly the same picture for each of the proofs! The pictures
all involved a disc of radius R centered at 0, a point z in the disc,
and some "intermediate" object between z and the boundary. In the case
of the first proof, the intermediate object was another point. In the
case of the second proof, the intermediate object was a disc around z
inside of the bigger disc. In the third proof, the intermediate object
was a circle of radius S between z and  DR(0). There is a need to keep the boundary of the
disc pushed away in all of these proofs.
DR(0). There is a need to keep the boundary of the
disc pushed away in all of these proofs.
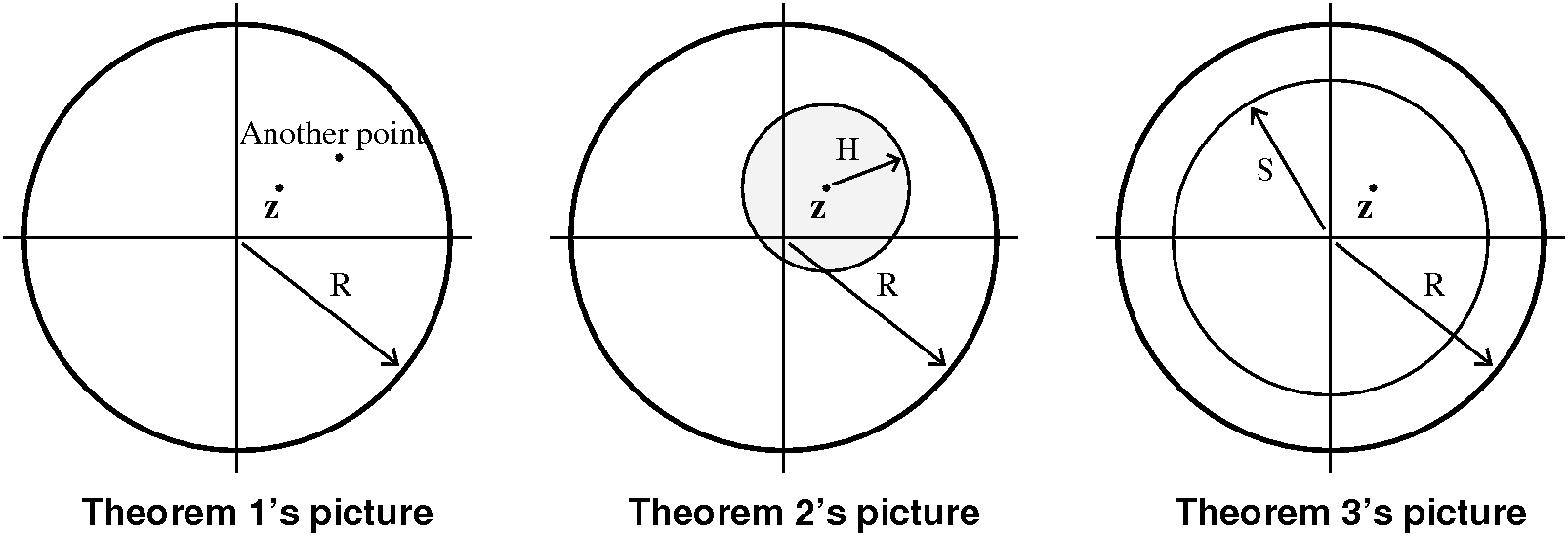
Theorem 1 If
f(z)= n=0
n=0 anzn,
then there exists R in [0,
anzn,
then there exists R in [0, ], such that if |z|<R,
], such that if |z|<R,
 n=0
n=0 anzn
converges absolutely. If S<R, then
anzn
converges absolutely. If S<R, then
 n=0
n=0 anzn
converges uniformly in when |z|<=S and therefore converge uniformly
on all K compact contained in {z with |z|<R}.
anzn
converges uniformly in when |z|<=S and therefore converge uniformly
on all K compact contained in {z with |z|<R}.
R is called the radius of convergence of the infinite
series. There is a "formula" called the
Cauchy-Hadamard formula for R in terms of the coefficients
an of the series. It implies standard calculus results such
as the Ratio Test and the Root Test. It is also generally strikingly
ineffective in actually determining a radius of
convergence!
Proof Take R=sup{|z|: supn>=0
|anzn|<  }. Certainly 0 is an "eligible" number, so the sup is taken over a non-empty set.
}. Certainly 0 is an "eligible" number, so the sup is taken over a non-empty set.
If R>0, take z with |z|<R. Then there exists z1
with |z1|<R and |z|<|z1|. Let A=supn>=0|anz1n|< . Thus
. Thus
| n=0
n=0 anzn|=<
anzn|=< n=0
n=0 |anzn|=
|anzn|= n=0
n=0 |an(z/z1)n(z1)n|=<
|an(z/z1)n(z1)n|=< n=0
n=0 |(z/z1)n|A<
|(z/z1)n|A< . The series for z converges absolutely, and therefore converges.
. The series for z converges absolutely, and therefore converges.
Now take S<R. Suppose we consider z with with |z|=<S. Then
|anzn|<=|an|Sn. We may
apply the Weierstrass M-test and get uniform convergence in the closed
disc of radius S. Notice that if K is a compact
subset of the open disc of radius R, then K is covered by the sequence
of open discs of radius R-(1/n), and therefore (finite subcover!), K
is contained in one of those discs, and we can take S to be that
R-1/n. So there is uniform convergence on any compact subset of
the disc of radius R.
Theorem 2 If
f= n=0
n=0 anzn,
then f is holomorphic in DR(0) (R as defined previously)
and
f´(z)=
anzn,
then f is holomorphic in DR(0) (R as defined previously)
and
f´(z)= n=0
n=0 nanz^{n-1}. (So
the latter infinite series converges also in DR, and its
sum is the derivative of f).
nanz^{n-1}. (So
the latter infinite series converges also in DR, and its
sum is the derivative of f).
Proof First let us recall
 n=0
n=0 nanzn-1
converges in DR(0) (you can refer to some textbooks or look
very carefully at what we will do.)
nanzn-1
converges in DR(0) (you can refer to some textbooks or look
very carefully at what we will do.)
Then let us calculate limh-->0(f(z+h)-f(z))/h carefully. We
will see that the limit exists equals
 n=0
n=0 nanzn-1.
Fix some H>0, so that |z|+H<R. We will consider h in C with
|h|<=H. Then
f(z+h)=
nanzn-1.
Fix some H>0, so that |z|+H<R. We will consider h in C with
|h|<=H. Then
f(z+h)= n=0
n=0 an(z+h)n=
an(z+h)n= n=0
n=0 an
an k=0n(Cnk)zn-khk. This
series in h converges absolutely and uniformly when |h|<=H
(consider that if we replace z by |z| and h by |h| it just becomes the
power series for f(|z|+|h|) (with an expansion using the Binomial
Theorem) inside the radius of convergence.
k=0n(Cnk)zn-khk. This
series in h converges absolutely and uniformly when |h|<=H
(consider that if we replace z by |z| and h by |h| it just becomes the
power series for f(|z|+|h|) (with an expansion using the Binomial
Theorem) inside the radius of convergence.
Now define
Qz(h)=(f(z+h)-f(z))/h= n=0
n=0 an
an k=1n(an)zn-kh^{k-1}.
k=1n(an)zn-kh^{k-1}.
You can compare this series to the series for f(z+h). It is almost the
same (there is a multiple of h missing and one other term). But if the
series for f(z+h) converges then this series is first, a subseries
(omit the hn terms in f(z+h), and then, a division by h. So
by comparison, this series also converges absolutely and
uniformly.
Therefore Qz(h) is a continuous function of h for
|h|<H. So limh-->0Qz(h)=Qz(0). And
if you look carefully, you will see that Qz(0) is the
series we wrote for f´(z). Please notice that we've shown the
series converges at least for all z in DR(0)
Corollary If
f(z)= n=0
n=0 anzn
converges, then an=fn(0)/n!.
anzn
converges, then an=fn(0)/n!.
Proof Repeatedly differentiate and evaluate the power
series. This corollary essentially states that a convergent power
series is the Taylor series at the origin of the function which
is the sum of the power series.
Theorem 3 If f is holomorphic in DR(0),then there
exists a sequence {an}n=0 of
complex numbers so that
f(z)=
of
complex numbers so that
f(z)= n=0
n=0 anzn
for all z in DR(0).
anzn
for all z in DR(0).
Proof Since |z|DS(0), the correctly oriented (counterclockwise!)
boundary of the circle of radius S centered at 0. Then (the Cauchy
Integral Formula!) f(z)={1/(2Pi i)} s[f(w)/(w-z)]dw. But
1/(w-z)=(1/w)[1/(1-{z/w})]=(1/w)
s[f(w)/(w-z)]dw. But
1/(w-z)=(1/w)[1/(1-{z/w})]=(1/w) n=0
n=0 (z/w)n. This
series converges uniformally on
(z/w)n. This
series converges uniformally on  DS(0), so that we can interchange sum and
integral. Therefore f(z)={1/(2Pi i)}
DS(0), so that we can interchange sum and
integral. Therefore f(z)={1/(2Pi i)} sf(w)/(w-z)dw=
sf(w)/(w-z)dw= n=0
n=0 {1/(2Pi i}(
{1/(2Pi i}( sf(w)/(w^{n+1}dw)zn. Notice (by
Cauchy's Theorem) each of the coefficients {1/(2Pi i}(
sf(w)/(w^{n+1}dw)zn. Notice (by
Cauchy's Theorem) each of the coefficients {1/(2Pi i}( sf(w)/(w^{n+1}dw) of the
power series does not depend on the radius: the value will be
the same for any S between 0 and R. So the power series representation
is the same for any z in DR(0).
sf(w)/(w^{n+1}dw) of the
power series does not depend on the radius: the value will be
the same for any S between 0 and R. So the power series representation
is the same for any z in DR(0).
Corollary fn(0)=n!/(2Pi i) sf(w)/(w^{n+1}dw where s is
the boundary of any circle around 0 inside DR(0).
sf(w)/(w^{n+1}dw where s is
the boundary of any circle around 0 inside DR(0).
We actually already proved this earlier in the course, when we
differentiated functions defined with (w-z)-k as an
integral kernel.
MAJOR RECOGNITION
All of the definitions of "holomorphic" are equivalent. That is,
suppose f:U-<C, where U is a open domain in C. Consider these statements.
- f=u+iv, u,v are in C1(U) and
ux=vy and uy=-vx
(Cauchy-Riemann equations).
- f is a C1 mapping from U to R2, and either
the Jacobian of f has all entries 0 or f is directly conformal
at each point (in the sense of the homework assignment: angles between
curves in the domain and range are preserved).
- limh-->0(f(z+h)-f(z))/h exists for all z in U.
- f has a local power series expression at all points of U. (This
turns out to be logically identical to: f has a power series expansion
centered at every point, and the radius of convergence of the
expansion is at least the distance to the boundary of U.)
- Suppose f is in C0(U). If R is any closed rectangle
contained entirely inside U (the boundary and the interior), then

 Rf(z)dz=0.
Rf(z)dz=0.
- Suppose f is in C2(U),
 Re f=0 & Im f is a homonic conjugate of Re f.
Re f=0 & Im f is a homonic conjugate of Re f.
- f is C
 & f´ exists.
& f´ exists.
That these are equivalent has mostly been proved. Here is one link not
yet done (a sort of converse to Cauchy's Theorem). This "link" has a
specific name.
Morera's Theorem Suppose U open and connected in C and f is a
continuous complex-valued function defined on U. Suppose that for all
all rectangles R with R contained in U (R means the rectangular box
with its inside!) we know 
 Rf(z)dz=0,
then f is holomorphic in U.
Rf(z)dz=0,
then f is holomorphic in U.
PICTURE HERE!
Proof The idea is to define a holomorphic F in U so that
F =f. Then by results just done today, the derivative f must be holomorphic.
We need only define F "locally". That is, just consider f on an open
disc in U. We define an antiderivative F in that open disc. The method
is something we've already done several times. Define F(z) to be the
line integral from the center of the circle along half the boundary of
a rectangle ending at z. Depending upon which half-rectangle you take,
each of the partial derivatives is easily seen to be equal to
f. Since the two paths give the same value (that's the key
hypothesis!) the results must match up which verifies the
Cauchy-Riemann equations. This argument is given in
detail on page 73 of the text.
It is also true that we didn't verify all details of the following,
which showns that we need not assume continuity of f´ in
the definition of holomorphic.
Goursat's Theorem If for all z in U,
limh-->0(f(z+h)-f(z))/h exists,then f is holomorphic.
We will verify this next time using Morera's Theorem.
| Friday,
October 5 | (Lecture #10) |
|---|
Notes by Jeffrey Amos, edited, with
some comments, by the instructor.
For Borel's theorem, please see here. For complex analysis, the most
important and interesting fact is in the very last paragraph on the
third page. I thought more about the proof presented of Borel's
Theorem over the weekend. I can now present a proof that is one
quarter the length, with much less insight. (Think vertically instead
of horizontally!) I will mention this in class. Which proof is
"better"? What is "better"?
Suppose we have a C function on [0, inf). From
Borel's theorem, we can extend this to a C
function on [0, inf). From
Borel's theorem, we can extend this to a C function
on the reals. This result is useful in differential topology, when one
might want to "patch together" C
function
on the reals. This result is useful in differential topology, when one
might want to "patch together" C functions.
functions.
Let {fn} be a sequence of functions. Let
Sn,k=sup|fn(x)-f(x)| where the sup is over x in
[-k,k]. Let
Sn,k,j=sup|f(j)n(x)-f(j)(x)|
where the sup is over x in [-k,k]. We say fn-->f is
locally uniform if Sn,k-->0 as n--> for all fixed k. We say
fn-->f (in C
for all fixed k. We say
fn-->f (in C ) is locally uniform if Sn,k,j-->0 as
n-->
) is locally uniform if Sn,k,j-->0 as
n--> for all fixed j, k. The
sequence fn(x)=x/n shows that these two are not the same.
Structural fact: if {fn} are C0 and
fn-->f locally uniformly, then f is C0. Also,
if {fn} are C
for all fixed j, k. The
sequence fn(x)=x/n shows that these two are not the same.
Structural fact: if {fn} are C0 and
fn-->f locally uniformly, then f is C0. Also,
if {fn} are C and fn-->f locally uniformly in C
and fn-->f locally uniformly in C , then f is C
, then f is C .
.
A norm on a vector space V is a function from V to R such that for
vectors v,w and real a:
i) ||v||>= 0 with equality iff v=0.
ii) ||av|| = |a| ||v||
iii)||v+w||<=||v||+||w||.
We can define a metric d by d(v, w)=||v-w||. C functions are a vector space, and we would like a metric such that
d(fn, f)-->0 iff fn-->(C
functions are a vector space, and we would like a metric such that
d(fn, f)-->0 iff fn-->(C ) f
is locally uniform. Unfortunately, no such vector space norm exists
with these properties. But we do have a metric, loosely defined by
d(f,g)=
) f
is locally uniform. Unfortunately, no such vector space norm exists
with these properties. But we do have a metric, loosely defined by
d(f,g)= (1/2sizeS_X(f-g)/(2^(-something)·(1+S_X(f-g)))
where the sum is over some countable enumeration of X,which is triples
n,k,j and the size is just the index of the enumeration
variable. It is not at all obvious that there is
no norm consistent with the metric space structure given by
this d. And, honestly, some thought is needed to see that the d(f,g)
defined coincides with locally uniform convergence of functions and
all of their derivatives. The "structure" of C
(1/2sizeS_X(f-g)/(2^(-something)·(1+S_X(f-g)))
where the sum is over some countable enumeration of X,which is triples
n,k,j and the size is just the index of the enumeration
variable. It is not at all obvious that there is
no norm consistent with the metric space structure given by
this d. And, honestly, some thought is needed to see that the d(f,g)
defined coincides with locally uniform convergence of functions and
all of their derivatives. The "structure" of C (R)
along with d(f,g), which provides a complete metric on the
vector space, with a neighborhood basis of convex sets, is called a
Frechet space.
(R)
along with d(f,g), which provides a complete metric on the
vector space, with a neighborhood basis of convex sets, is called a
Frechet space.
In the case of R and C, locally uniform convergence is the same as
uniform convergence on all compact subsets. That's because R and C are
locally compact. The convergence is actually more often called
uniform convergence on compact subsets (ucc).
Returning to complex analysis, consider all polynomials in z,
C[z}. C[z] is well-understood (all finite sums of monomials, or,
multiplicatively, assuming C is algebraically closed (!), the product
of linear polynomials). Next consider all power series in z,
C[[z]]. This is sort of all complex sequences. It has a ring structure
where addition is coordinate by coordinate, but multiplication is
somewhat weird when considered abstractly. The product of two
sequences of complex numbers, (an)n>=0 and
(bn)n>=0, is a third sequence,
(cn)n>=0, with
cn= j=0najbn-j. The
product is not the coordinate-wise product. This is inherited
from the intermediate ring, which we will be studying, the ring of
convergent power series. It is our goal to find a subring of
the power series in z such that all functions in the subring are
holomorphic, and any holomorphic function can be locally represented
as a series in the subring.
j=0najbn-j. The
product is not the coordinate-wise product. This is inherited
from the intermediate ring, which we will be studying, the ring of
convergent power series. It is our goal to find a subring of
the power series in z such that all functions in the subring are
holomorphic, and any holomorphic function can be locally represented
as a series in the subring.
We will prove the following fundamental fact: Given
 r=0
r=0 arzr,
there exists an R in [0,
arzr,
there exists an R in [0, ] such that if |z|>R, then the
series divergences, and if |z|<R, the series converges absolutely.
Furthermore, if S
"Examples" (The reason for the quotes is that a naive person
would need to think quite a bit to verify them!).
] such that if |z|>R, then the
series divergences, and if |z|<R, the series converges absolutely.
Furthermore, if S
"Examples" (The reason for the quotes is that a naive person
would need to think quite a bit to verify them!).
ar=r!, then R=0.
ar=1, then R=1.
ar=1/r!, then R= .
.
The motivation for this comes from geometric series. If r<1, then
 n=0
n=0 wn converges locally uniformly to
1/(1-w) when $|w|<1.
wn converges locally uniformly to
1/(1-w) when $|w|<1.
Proof
1+w+w2+...+wk=(1-wk+1/(1-w) when w is
not 1. But limk--> wk+1=0 for
|w|<1, and this limit is uniform in compact subdiscs of the unit
disc. Therefore, since
|
wk+1=0 for
|w|<1, and this limit is uniform in compact subdiscs of the unit
disc. Therefore, since
| n=0Nwn|<=
n=0Nwn|<= n=0N|w|n,
we're done (Weierstrass).
n=0N|w|n,
we're done (Weierstrass).
There are several methods for specifying the R, called the radius
of convergence, for
 r=0
r=0 arzr. There
is a classical formula (which sometimes provides very little
information) called the Cauchy-Hadamard
formula. Here R will be the following more irritating number,
which has more easily discerned information:
arzr. There
is a classical formula (which sometimes provides very little
information) called the Cauchy-Hadamard
formula. Here R will be the following more irritating number,
which has more easily discerned information:
R=sup of z in C with
supr>=0|arzr|< . R is
the sup of those z s for which the individual terms of the power
series are bounded. Notice that if z=0, the terms are always bounded
(all but the first are 0, after all!). So the sup is taken over a
non-empty set of complex numbers.
. R is
the sup of those z s for which the individual terms of the power
series are bounded. Notice that if z=0, the terms are always bounded
(all but the first are 0, after all!). So the sup is taken over a
non-empty set of complex numbers.
| Tuesday,
October 2 | (Lecture #9) |
|---|
Notes by Gene Kim, edited, with
some comments, by the instructor.
First, the lecturer berated us for our solutions to #2 (most of the
students anyway). The text should have indicated
that the problem was an explicit method for getting an antiderivative
of a holomorphic function in a disc (indeed, in a star-shaped open
set). The "recipe" given can be independently verified (with FTC or
equivalent tools) as an antiderivative. Most students quickly solved
the problem by appealing to the already known result that, in discs,
holomorphic functions have antiderivatives. The problem in the text
uses a now-standard technique for verifying what's called the
Poincaré Lemma about closed and exact differential forms. One
reference is Spivak's text, Calculus on Manifolds.
The overall goal of this week is, almost, to turn 503 into an algebra
course. Holomorphic functions are a rather peculiar collection of
rings. But this is postponed, and we will have an excursion
(digression?) into some associated topics.
The scribe would like to note that a reference for the well-known
material of the lecture is Rudin's Principles of Mathematical
Analysis, Chapter 6(?).
Last time, we showed that O(U), the holomorphic functions defined on
an open subset U of C, is actually a subset of
C (U). Before giving another characterization of
holomorphic functions, maybe we should learn a bit about
C
(U). Before giving another characterization of
holomorphic functions, maybe we should learn a bit about
C , and, on the way, review convergence ideas for
functions. It is interesting to note that the convergence ideas we
will discuss, which are now so clear to define and use, were
historically arrived at with numerous stumbles (!) and errors (!!). A
century and a half ago, the "correct" ideas for convergence were not
totally clear. The lecturer hopes that this is an encouraging
statement to students at the start of their research careers. We will
consider several examples of functions in C
, and, on the way, review convergence ideas for
functions. It is interesting to note that the convergence ideas we
will discuss, which are now so clear to define and use, were
historically arrived at with numerous stumbles (!) and errors (!!). A
century and a half ago, the "correct" ideas for convergence were not
totally clear. The lecturer hopes that this is an encouraging
statement to students at the start of their research careers. We will
consider several examples of functions in C (R).
(R).
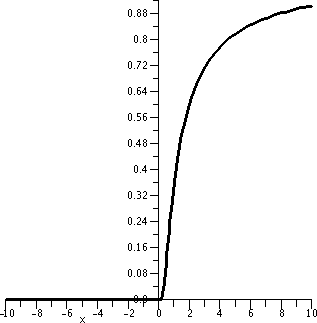
Begin with A ...
We create A in C (R), defined piecewise: A(x)=0 if x<0
and A(x)=e-1/x if x>0. Also, A(0)=0.
(R), defined piecewise: A(x)=0 if x<0
and A(x)=e-1/x if x>0. Also, A(0)=0.
Is it "clear" that A is C ? The continuity of A at
non-zero x should be clear. When x=0, we need to verify that
limx-->0+A(x)=0. This is the same as
limx-->0+e-1/x=0, but if 1/x=w, we
have the limit limw-->+
? The continuity of A at
non-zero x should be clear. When x=0, we need to verify that
limx-->0+A(x)=0. This is the same as
limx-->0+e-1/x=0, but if 1/x=w, we
have the limit limw-->+ e-w which is
certainly 0. (The reason for going through this is so that a more
complicated limit, coming up, will be easier.)
e-w which is
certainly 0. (The reason for going through this is so that a more
complicated limit, coming up, will be easier.)
Let's try for C1: A´(x) certainly exists for x not
zero. When x<0, A´(x)=0, and when x>0,
A´(x)=e-1/x(1/x2). If we wish to consider
A´(0), we should look at the official definition. Since A(0)=0,
we have to consider limx-->0A(x)/x. As x-->0-,
this is clear 0. What about from the right? Well,
limx-->0+A(x)/x is the same as
limx-->0+e-1/x(1/x) and this is the
same as (with 1/x=w)
limw-->+ we-w=limw-->+
we-w=limw-->+ w/ew
which, with L'Hôpital's Rule, is 0.
w/ew
which, with L'Hôpital's Rule, is 0.
Therefore A is C1. We could continue or think
inductively. To go from Ck to Ck+1, realize that
a formula for A(k)(x) when x>0 looks like
e-1/xP(1/x) where P is some one variable real
polynomial. The same trick as before (change variables, use
L'Hôpital) shows that
limx-->0+e-1/xP(1/x)=0. So A is
C .
.
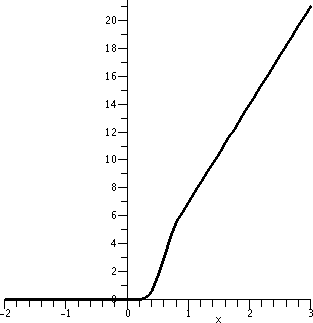
And now D, which is for Digression
We need this to clarify some previous comments. Define D, which is in
C (R), by D(x)=xC(x). This function is 0 for x<0,
and is strictly increasing (look at its derivative!) for x>=0. We
can use this function to define a C
(R), by D(x)=xC(x). This function is 0 for x<0,
and is strictly increasing (look at its derivative!) for x>=0. We
can use this function to define a C parameterized
curve in R2.
parameterized
curve in R2.
Consider s:R-->R2 defined by s(t)=(D(t),D(-t)). We see that
s is C and is also one-to-one (the two D's work to
show that in different parts of the domain). However, s is a "bad"
curve, or at least unintuitive. The image of s is L. By that we mean the union
of the positive x-axis, the positive y-axis, and 0. The image of this
"smooth curve" seems to have a corner. The problem is that the
parameterizing variable doesn't even see (?) the corner. It's velocity
vector is 0 there. Think about this.
and is also one-to-one (the two D's work to
show that in different parts of the domain). However, s is a "bad"
curve, or at least unintuitive. The image of s is L. By that we mean the union
of the positive x-axis, the positive y-axis, and 0. The image of this
"smooth curve" seems to have a corner. The problem is that the
parameterizing variable doesn't even see (?) the corner. It's velocity
vector is 0 there. Think about this.
People who study differential geometry don't like this, so a slightly
different kind of curve is used:
Definition s is a regular curve if is
C and s´ is never zero.
and s´ is never zero.
L is not the
image of a regular curve. This is not totally obvious (one
verification uses the {Inverse/Implicit} Function Theorem). Students
should try to verify this, and if they cannot, please see the
instructor.
Partitions of unity
The following was mentioned with no proof. The proof takes some
careful verification (see any reasonable differential topology text),
and really would be too far from our discussion of complex
analysis. If {Ua}a in A is an open cover of R,
then there is a C partition of unity which is
subordinate to {Ua}a in A: a collection
of functions {fa} so that:
partition of unity which is
subordinate to {Ua}a in A: a collection
of functions {fa} so that:
Each fa is C ,
0=<fa(x)<=1 for all x in R, and supp(fa)
is contained in Ua. The supports are locally finite
(each x in R has a neighborhood in which at most finitely many
fa's are not 0) and
,
0=<fa(x)<=1 for all x in R, and supp(fa)
is contained in Ua. The supports are locally finite
(each x in R has a neighborhood in which at most finitely many
fa's are not 0) and  a in
Afa(x)=1 for all x in R.
a in
Afa(x)=1 for all x in R.
That's a great deal to absorb. Such functions are usually used to
"localize" arguments, much like characteristic functions of measurable
sets are used to restrict attention to what's happening where those
functions are non-zero. When we multiply "something" by one of the
fa's, we won't change the smoothness of the something.
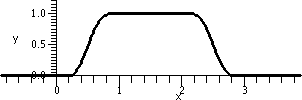 Maybe a true smooth "bump"
Maybe a true smooth "bump"
Finally, the last in this sequence of examples. Look at C, defined
previously. For x>1, C is constant. That
constant, by the way, is about 0.007029858407.
Who
cares? We should remember that The
purpose of computing is insight, not numbers as Richard
Hamming wrote. There's no insight in this number. It is the
slope of the D function for x>1. Sigh.
So
consider the smooth function defined by the formula C(x)C(3-x) divided
by the square of that constant (we've got to adjust two copies of
C). A graph of this function is shown to the right. You don't have to like this function. In fact, I am
almost sure that almost no mathematician whose career was earlier than
the 20th century would like this function.
Properties The support of this C function is
[0,3], its values are all non-negative, and it is 1 on [1,2]. It is
increasing on [0,1] and decreasing on [2,3].
function is
[0,3], its values are all non-negative, and it is 1 on [1,2]. It is
increasing on [0,1] and decreasing on [2,3].
I hope that it is clear by scaling, etc., we can do the following:
given any a<b<c<d, create a C function
whose suppose is [a,d], which is always non-negative, which is 1 on
[b,c], and which is increasing on [a,b] and decreasing on [c,d]. These
are called smooth bump functions.
function
whose suppose is [a,d], which is always non-negative, which is 1 on
[b,c], and which is increasing on [a,b] and decreasing on [c,d]. These
are called smooth bump functions.
A theorem, finally!
This result is an indication that there are so many
C functions, and that they can do almost anything!
functions, and that they can do almost anything!
Theorem (E. Borel) Given any sequence of real numbers
{an}, there exists f in C (R) with
f(n)(0)=an for all n>=0.
(R) with
f(n)(0)=an for all n>=0.
"Proof"
f(x)= n=0
n=0 (an/n!)xn. not quite...
(an/n!)xn. not quite...
The reason for "not quite" is that the series need not converge for
any value of x except 0. But now we have an excuse (!) to study such
convergence.
Questions of convergence ...
Suppose X is a metric space. Then {xn}, a sequence in X,
converges to x (its limit is x) if for all e>0, there
exists N(e) such that if n>N(e), then d(xn,x)<e.
This definition requires us to "know" somehow the limit, x, of the
sequence. We can supplement it with an "internal" criterion for
convergence, depending only on the sequence: A sequence
{xn} is Cauchy if for all e>0, there is M(e) such
that if n1, n2 > M, then
d(xn1,xn2)<e. Every convergent
sequence is Cauchy, but the converse is not necessarily true. The
Cauchy idea is useful (it is usually called the Cauchy
criterion), so we define: a metric space is complete if all
Cauchy sequences converge. My favorite complete metric spaces are R
and C and a few other function spaces we will meet later.
Convergence of functions
Let {fn} and f be functions from X to R (or C).
fn converges pointwise to f if for all x in X,
limn--> fn(x)=f(x). {fn}
converges uniformly to f if for all e>0, there exists N such
that if n>N, then |fn(x)-f(x)|<e for all x.
fn(x)=f(x). {fn}
converges uniformly to f if for all e>0, there exists N such
that if n>N, then |fn(x)-f(x)|<e for all x.
Uniform
convergence implies pointwise convergence. The converse is not
true. For example, the sequence xn converges pointwise but
not uniformly to 0 on the open interval (0,1).
Big result
We care about this because of the following proposition:
Theorem If {fn} is continuous from (X,d) to R (or
C) and {fn} converges uniformly to f, then f is continuous.
Proof We need to show that, given e>0 and x in X, there is
d>0 so that if y is in X and d(x,y)<d, then
|f(x)-f(y)|<e. Since {fn} converges uniformly to
f, there is N so that if n>N, |fn(w)-f(w)|<e/3. Fix
one such n greater than N. That fn is continuous on X, and
more precisely, continuous at x in X, so there is d>0 so that any y
in X with d(x,y)<d must satisfy
|fn(y)-fn(y)|<e/3.
Now consider what happens if d(x,y)<d:
|f(x)-f(y)|=<|f(x)-fn(x)|+|fn(x)-fn(y)|+|fn(y)-f(y)|<e/3+e/3+e/3=e
and we are done.
Pointwise convergence does not generally "transmit" continuity:
consider xn on [0,1]. The pointwise limit is a function
which is 0 for x<1 and 1 for x=1: not continuous.
{fn} converges locally uniformly to f if for all x
in X, there exists a neighborhood Nx such that
fn|Nx converges uniformly to
f|Nx.
Proposition A locally uniformly convergent sequence of
continuous functions has a continuous limit.
Now on to series!
 j=0
j=0 fj(x)
converges pointwise if the sequence {FN} converges
pointwise, where
FN(x)=
fj(x)
converges pointwise if the sequence {FN} converges
pointwise, where
FN(x)= j=0Nfj(x)
(a partial sum of the infinite series).
j=0Nfj(x)
(a partial sum of the infinite series).
 j=0
j=0 fj(x)
converges uniformly if the sequence of partial sums,
{FN} converges uniformly.
fj(x)
converges uniformly if the sequence of partial sums,
{FN} converges uniformly.
 j=0
j=0 fj(x)
converges locally uniformly if the sequence of partial sums
converges locally uniformly.
fj(x)
converges locally uniformly if the sequence of partial sums
converges locally uniformly.
 j=0
j=0 fj(x)
converges absolutely if
fj(x)
converges absolutely if
 j=0
j=0 |fj(x)|
converges pointwise.
|fj(x)|
converges pointwise.
Of course, convergence does not imply absolute convergence
( j=0
j=0 (-1)n/n), but
the converse is true: absolute convergence does imply convergence
(this uses the Cauchy criterion, and students should be able to write
out the argument).
(-1)n/n), but
the converse is true: absolute convergence does imply convergence
(this uses the Cauchy criterion, and students should be able to write
out the argument).
Weierstraß
Theorem (Weierstrass M-Test)
Suppose that {aj} is a convergent series of non-negative
numbers:
 j=0
j=0 aj<
aj< .
Also suppose that there exists M>0 such that
|fj(x)|=<Maj for all x in X. Then
.
Also suppose that there exists M>0 such that
|fj(x)|=<Maj for all x in X. Then
 j=0
j=0 fj
converges uniformly and absolutely for all x in X.
fj
converges uniformly and absolutely for all x in X.
How about the proof?
Now we play around with the function for "Proof" of Borel's
Theorem. I'll use CHIA to be the characteristic function of
A, a subset of R, so CHIA(x) is 1 if x is in A and 0
otherwise.
Consider
f(x)= j=0
j=0 {(an/n!)xn}·(CHI[-rn,rn](x)),
where In=[-rn,rn] is the interval
whre |(an/n!)xn|<1/2n (there is
such an interval, since the monomial function is 0 at 0). Then, the
series describing f converges uniformly and absolutely. However f is
not C0. So we need to "cut off" things more smoothly -- we
need to introduce smooth convergence multipliers.
{(an/n!)xn}·(CHI[-rn,rn](x)),
where In=[-rn,rn] is the interval
whre |(an/n!)xn|<1/2n (there is
such an interval, since the monomial function is 0 at 0). Then, the
series describing f converges uniformly and absolutely. However f is
not C0. So we need to "cut off" things more smoothly -- we
need to introduce smooth convergence multipliers.
Suppose b is a specific fixed smooth bump function: b(x) is 0 for
|x|>1 and 1 if |x|<1/2. Also, b is between 0 and 1 otherwise,
even increasing in [-1,-1/2] and decreasing in [1/2,1].
Consider
f(x)= j=0
j=0 {(an/n!)xn}·b(rnx). Each
summand is C
{(an/n!)xn}·b(rnx). Each
summand is C and the series converges absolutely
and uniformly (comparing with a geometric series with ratio 1/2!). So
f is C0, and f(0)=a0. What the heck happens when
we differentiate? We need a theorem, maybe.
and the series converges absolutely
and uniformly (comparing with a geometric series with ratio 1/2!). So
f is C0, and f(0)=a0. What the heck happens when
we differentiate? We need a theorem, maybe.
Differentiating a sum
Proposition Suppose that {fn} is a sequence of
C1 functions on R with fj converging uniformly
to f and fj´ converging uniformly to g. Then f is
C1 and f´=g.
Proof We'll use the fact (previously mentioned in connection
with the ML inequality) that integration can be "exchanged" with
limits of uniformly convergent sequences of functions. Here we know
fj(x)-fj(0)= 0xfj´(t)dt by FTC.
Now take limj-->
0xfj´(t)dt by FTC.
Now take limj--> . The result (after the mentioned
interchange!) is
f(x)-f(0)=
. The result (after the mentioned
interchange!) is
f(x)-f(0)= 0xf´(t)dt=
0xf´(t)dt= 0xg(t)dt
0xg(t)dt
and now the "other" (?) part of FTC (differentiability of a variable
upper bound in an integral) implies that f is differentiable, and that
its derivative is g.
You may notice that we don't really use all the information about the
convergence of f. The conclusion still is valid if we only know
fj(0) converges to f(0).
But then we can only get "out" that the sequence of functions,
{fj} will converge locally uniformly to f. EXAMPLE?
The discussion of the proof of Borel's Theorem will continue, and then
we will return to complex analysis.
| Friday,
September 28 | (Lecture #8) |
|---|
Notes by Jay Williams, edited, with
some comments, by the instructor.
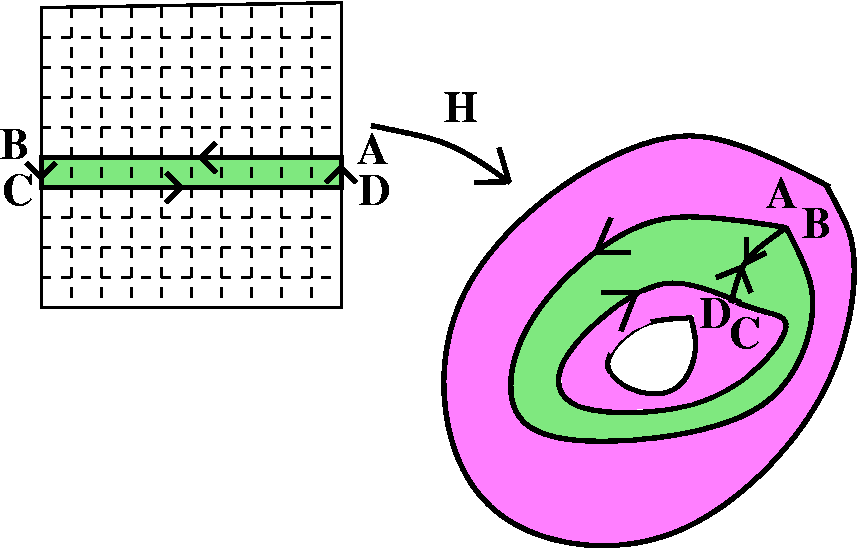
Mr. Kim's (justified) complaint
In the proof of Cauchy's Theorem from last class, we showed that given
two C0 curves in U which are homotopic in U, and a function
f holomorphic in U, the line integral around the two curves is equal.
 To do this, we split up the homotopy diagram into tiny rectangles,
around which we knew the integrals were 0. The sides of the
rectangles in the interior canceled each other out, leaving the
integrals along the sides of the homotopy diagrams. The line integrals
at the top and bottom of the diagram are the two we
claimed to be equal. But Mr. Kim wondered, what about the integrals
on the sides of the diagram? Where did they go?
To do this, we split up the homotopy diagram into tiny rectangles,
around which we knew the integrals were 0. The sides of the
rectangles in the interior canceled each other out, leaving the
integrals along the sides of the homotopy diagrams. The line integrals
at the top and bottom of the diagram are the two we
claimed to be equal. But Mr. Kim wondered, what about the integrals
on the sides of the diagram? Where did they go?
We neglected to take note of the fact that since the homotopy H was
set up so that H(0,t)=H(1,t) for all t, meaning the sides of the
diagram are curves with the same endpoints. Since they are traversed
in opposite directions, they create a closed curve, around which we
know the integral is 0. And that is where those integrals went.
The accompanying diagram shows the
situation. The ABCD integral is 0 using the reasoning of the last
lecture. The integrals from B to C and from D to A cancel, since they
are pointwise the same curve but described in reverse order. Therefore
the integral from B to A is equal to the integral from C to D (all the
ordering works!).
An analysis course has inequalities. Why wasn't the most important inequality in complex analysis stated and proved?
The ML Inequality Suppose s:[a,b]-->C is a C1
curve, and f is continuous on s([a,b]). Then | sf(z)dz|<=ML, where
M=(supz in s([a,b])|f(z)|) and L=length of s, which is
sf(z)dz|<=ML, where
M=(supz in s([a,b])|f(z)|) and L=length of s, which is  |s´(t)|dt.
|s´(t)|dt.
Proof | sf(z)dz|= |
sf(z)dz|= | ab|f(s(t))s´(t)dt|<=
ab|f(s(t))s´(t)dt|<= ab|f(s(t))| s´(t)|dt<=
(supz in s([a,b])|f(z)|)
ab|f(s(t))| s´(t)|dt<=
(supz in s([a,b])|f(z)|) |s´(t)|dt. (Sort of L1 and
L
|s´(t)|dt. (Sort of L1 and
L .)
.)
This works if s:[a,b]-->C is a piecewise C1 curve.
An application of the above inequality:
Proposition Suppose {fj} is a sequence of continuous
functions on s([a,b]) and fj converges uniformly to f on
s([a,b]). Then limj-->
 sfj(z)dz=
sfj(z)dz= slimj-->
slimj--> fj(z)dz.
fj(z)dz.
This is the only limit interchange theorem in the course. I hope.
Here's the proof. What's the theorem?
Proof Suppose Q(z)= sA(t)/(t-z)ndt, where A is C0
on the image of s, and z is not in the image of s. Take h so small
that if |h|<=E, then |z+h| is in U.
sA(t)/(t-z)ndt, where A is C0
on the image of s, and z is not in the image of s. Take h so small
that if |h|<=E, then |z+h| is in U.
(Q(z+h)-Q(z))/h= sA(t)((1/h)(1/(t-z-h)n1/(t-z)n)dt=
sA(t)((1/h)(1/(t-z-h)n1/(t-z)n)dt= s(A(t)/h)((t-z)n-(t-z-h)n)/[(t-z-h)n(t-z)n]dt.
A(t) is not "where the action is".. So let's look at where the action
is. (Here Cn,j is the n,j binomial coefficient.)
s(A(t)/h)((t-z)n-(t-z-h)n)/[(t-z-h)n(t-z)n]dt.
A(t) is not "where the action is".. So let's look at where the action
is. (Here Cn,j is the n,j binomial coefficient.)
(((t-z)n-(t-z-h)n)/[(t-z-h)n(t-z)n]=((t-z)n j=0nCn,j(t-z)n-j(-h)j)/(h(t-z-h)n(t-z)n=
j=0nCn,j(t-z)n-j(-h)j)/(h(t-z-h)n(t-z)n= j=1nCn,j(t-z)n-j(-h)j)/[h(t-z-h)n(t-z)n]=
j=1nCn,j(t-z)n-j(-h)j)/[h(t-z-h)n(t-z)n]= j=1n(Cn,j(t-z)n-j(-h)j-1)/[(t-z-h)n(t-z)n].
j=1n(Cn,j(t-z)n-j(-h)j-1)/[(t-z-h)n(t-z)n].
In this last expression, there are a few things to note. We treat z
as fixed. h is in the closure of the disk of radius E centered at the
origin. t is s(w), for w in [a,b], i.e., t is in s([a,b]).
Treating this last expression as a function F(h,t), these observations
lead to the conclusion that F(h,t) is continuous.
More precisely, F:(The closure of the disk of radius E centered at the
origin)xs([a,b])-->C is continuous. Since the domain of F is a
compact set, F is uniformly continuous: given r>0, there exists
d>0 such that if |h1-h2|<d and
|t1-t2|1,t1)-F(h2,t2)|
What is F(0,t)?
F(0,t)=(n(t-z)n-1)/(t-z)2n. F(h,_) converges
uniformly to F(0,_) as h goes to 0, where _ is some t in s([a,b]). So
we may interchange limit and integral: limh-->0 sA(t)((1/h)(1/(t-z-h)n)(1/(t-z)n)dt=
sA(t)((1/h)(1/(t-z-h)n)(1/(t-z)n)dt= slimh-->0A(t)F(h,t)dt=
slimh-->0A(t)F(h,t)dt= sA(t)F(0,t)dt.
sA(t)F(0,t)dt.
What's the theorem?
Theorem Suppose s:[a,b]-->C is a piecewise C1 curve,
and A is continuous on s([a,b])). Define Q(z)= sA(t)/(t-z)ndt.
(Here n is a natural number.) Then Q is holomorphic on C\{s([a,b])} and
Q´(z)=
sA(t)/(t-z)ndt.
(Here n is a natural number.) Then Q is holomorphic on C\{s([a,b])} and
Q´(z)= snA(t)/(t-z)n+1dt. (A homework problem
was a version of this!)
snA(t)/(t-z)n+1dt. (A homework problem
was a version of this!)
The most important specific use will be when A(t)=1, n=1, s a closed
curve. Then Q/(2Pi i) is the "winding number". We will discuss
this later.
Recall the Cauchy Integral Formula: Given an open set U, with a closed
disk with radius r and center p contained in U, f holomorphic on U,
and z in the interior of the disk, then f(z)=(1/2i) bdry of the disc(f(t)/(t-z))dt.
bdry of the disc(f(t)/(t-z))dt.
Using the above Theorem combined with this fact, we get a
Cauchy Integral Formula for Derivatives. Given the same
hypotheses as the Cauchy Integral Formula, we get that f is
C on U, f(n) is holomorphic on U for all
n, and f(n)(z)=n!/(2Pi i)
on U, f(n) is holomorphic on U for all
n, and f(n)(z)=n!/(2Pi i) bdry of the disc(f(t)/(t-z)n+1)dt.
bdry of the disc(f(t)/(t-z)n+1)dt.
But wait, here's something curious. From above, we get
f´(z)=(1/2Pi i) bdry of the disc(f(t)/(t-z)2)dt. But
also we could use the Cauchy Integral Formula directly:
f´(z)=1/(2Pi i)
bdry of the disc(f(t)/(t-z)2)dt. But
also we could use the Cauchy Integral Formula directly:
f´(z)=1/(2Pi i) bdry of the disc(f´(t)/(t-z))dt
(since f´ is also holomorphic). So are these the same?
Integration by parts should convince you that yes, they are.
bdry of the disc(f´(t)/(t-z))dt
(since f´ is also holomorphic). So are these the same?
Integration by parts should convince you that yes, they are.
Two Awesome Consequences
#1
Suppose we have u(x,y), u:U-->R, U open in C, u is C2(U),
and  u=0. Take p in U with
E>0 so that the open disk of radius E with center p is contained in
U. Suppose
u=0. Take p in U with
E>0 so that the open disk of radius E with center p is contained in
U. Suppose  u=0 in the open
disk of radius with center p. This means there
u=0 in the open
disk of radius with center p. This means there  xxu+
xxu+ yy=0. Then we saw
earlier that there exists a function v that is C2 in the
disk so that u+iv is holomorphic on the disk (v is a "harmonic
conjugate" of u). From what was just discussed we know now that u+iv
is C
yy=0. Then we saw
earlier that there exists a function v that is C2 in the
disk so that u+iv is holomorphic on the disk (v is a "harmonic
conjugate" of u). From what was just discussed we know now that u+iv
is C on the disk, so u is C
on the disk, so u is C in
the disk and Conclusion u is C
in
the disk and Conclusion u is C on all of U.
on all of U.
This is a case of Weyl's
Lemma. On a related note, here is an oral exam at the Courant
Institute: Can you prove Weyl's Lemma? How many ways?
#2
Suppose U is a simply connected open set in C. Now we know if f is
holomorphic on U, there exists an F holomorphic on U such that
F´=f. We proved this on an open disk using the Fundamental
Theorem of Calculus. We can do this on U because of the simple
connectedness. Suppose s is a curve "from" a fixed z0 to z.
If F(z)= sf(z)dz, we
know F(z) does not depend on our choice of s since any other curve
with the same endpoints will combine with s to create a closed curve,
which is homotopic to a point ("simply connected"!). So we change s
to a curve that we can use FTC on (it would end up with a vertical
line segment or a horizontal line segment).
sf(z)dz, we
know F(z) does not depend on our choice of s since any other curve
with the same endpoints will combine with s to create a closed curve,
which is homotopic to a point ("simply connected"!). So we change s
to a curve that we can use FTC on (it would end up with a vertical
line segment or a horizontal line segment).
Given U simply connected and open in C and an f holomorphic in U which
never vanishes, there exists a function L holomorphic in U such that
eL(z)=f(z), and for all n in the natural numbers, there
exists a function h holomorphic in U such that hn=f. You
may recall that we gave a proof of this for the unit disk, but not
very well. Well, with only one huge hole. We know more now, specifically that f
has a holomorphic derivative on U, so we can do it again and be right
this time. Remember the idea was to define g(z)=f´(z)/f(z). g
is holomorphic, since f and f’ both are and f never vanishes. This
means there is a G(z) such that G´(z)=g(z). Then exp(G)=f (or
almost, with possible correction by a multiplicative constant). Also,
(exp(G))´=(f´/f)exp(G), compute the derivative of
f/eg, etc. G is the L promised above.
 Example
Example
Look at the polar curve D given by the equation r = e in R^2. This is
a equiangular
spiral. It spirals around the origin infinitely often outside of
any disc. As z-->0, it spirals infinitely often around the origin
also. The curve and the origin together, DU{0}=X, is
closed in R2, so U=C\X is open in C. z is holomorphic in
U, z is not 0 in U, and U is simply connected. (Clearly. Well okay, a
little more on this later.) So by above, there exists a function L
such that exp(L(z))=z in U: eL(z)=z. We'll write
L(z)="log"(z) here.
in R^2. This is
a equiangular
spiral. It spirals around the origin infinitely often outside of
any disc. As z-->0, it spirals infinitely often around the origin
also. The curve and the origin together, DU{0}=X, is
closed in R2, so U=C\X is open in C. z is holomorphic in
U, z is not 0 in U, and U is simply connected. (Clearly. Well okay, a
little more on this later.) So by above, there exists a function L
such that exp(L(z))=z in U: eL(z)=z. We'll write
L(z)="log"(z) here.
Lets look at this "log"(z). Since exp is 2Pi i periodic, given
one "log" there will be infinitely many others. But we can adjust or
select so that "log"(2)=log(2), a value of the standard, ordinary
log. But when you follow the spiral around to get to another value on
the real axis, you gain 2Pi i,
e.g. "log"(800)=log(800)+2Pi i.
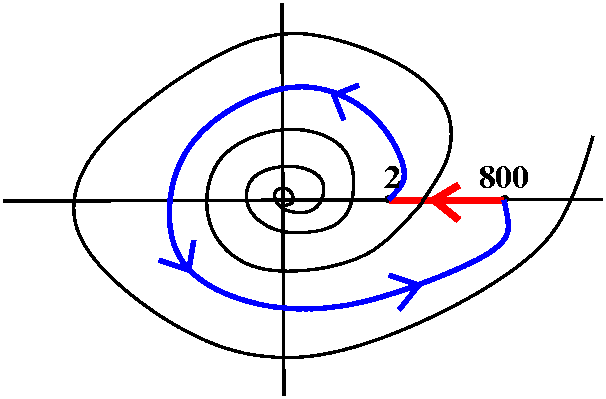 Let's give the acute reasoning of Ms. Naqvi here. So let's go from 2 to
800. One way of doing this is to get a path, s, from 2 to 800 in U,
and then "log"(800)=log(2)+
Let's give the acute reasoning of Ms. Naqvi here. So let's go from 2 to
800. One way of doing this is to get a path, s, from 2 to 800 in U,
and then "log"(800)=log(2)+ s(1/z)dz. But follow that path with the line
segment from 800 to 2 on the real axis. This is a curve around 0, and
by Cauchy's Theorem (it is homotopic to a circle around the origin)
the integral over the curve followed by the line segment of 1/z is
2Pi i. The line segment integral is a standard real integral, and
its value is log(2)-log(800). It goes "backwards", so we indeed do get
"log"(800)=log(800)+2Pi i.
s(1/z)dz. But follow that path with the line
segment from 800 to 2 on the real axis. This is a curve around 0, and
by Cauchy's Theorem (it is homotopic to a circle around the origin)
the integral over the curve followed by the line segment of 1/z is
2Pi i. The line segment integral is a standard real integral, and
its value is log(2)-log(800). It goes "backwards", so we indeed do get
"log"(800)=log(800)+2Pi i.
Yes, the picture is
distorted.
"log" will give you "sqrt" in U, defined by
"sqrt"(z)=e((1/2)"log"(z). "sqrt"(2) will be sqrt(2), but
"sqrt"(800) will be -sqrt(800) since ePi i=-1. "sqrt"
will alternate in sign on each piece of the real axis as you go out to
+ or to 0. The sign changes each time the spiral is crossed.
or to 0. The sign changes each time the spiral is crossed.
Classically speaking, we have just shown that there is a branch of log
in U. And U's simple connectedness follows from the fact that the
image of any curve in U is compact. So any curve will be bounded away
from 0 and away from " " -- it will be in between a finite
number of loops of the spiral.
" -- it will be in between a finite
number of loops of the spiral.
Homework remarks
Please note that problem 2 of assignment 1 provides yet another
characterization of holomorphicity. A C1 function is
holomorphic if its Jacobian is either identically 0 or if it locally
is orientation preserving and preserves angles between curves (it is
"directly conformal" [the adverb "directly" is frequently
omitted]). This is because the Jabobians of such mappings implicitly
imply the Cauchy-Riemann equations.
Also please note that A+B<C+D does not provide enough information to conclude that
A<B. Sigh.
| Tuesday,
September 25 | (Lecture #7) |
|---|
Notes by Hernan Castro, edited, with
some comments, by the instructor.
The main goal of this lecture is to prove Cauchy's Theorem, so we
start at the very beginning, by given a definition of the integral
over a closed C^0 curve:
Basic hypothesis U a open subset of C, f a holomorphic function
in U and s:[a,b]->U a C0 curve in U
And we want each of the following items to be possible
- A partition of the [a,b] interval:
a=t0<t1<...<tn-1<tn=b
such that there exists a collection of open discs in U:
Drj(zj) such that
s([tj-1,tj]) is contained in
Drj(zj) for all j=1,...,n.
- A collection of holomorphic antiderivatives of f in each disc:
Fj holomorphic in U and (Fj)´ = f in
Drj(zj).
- And this "thing":
F1(s(t1))-F1(s(t0))+...+Fj(s(tj))-Fj(s(tj-1))+...+Fn(s(tn))-Fn(s(tn-1)).
This is the "Thing Formula".
From the previous lectures, we already know that (a) is possible (the
Lebesgue Number discussion we had the previous lecture) and also (b)
is possible (the Poincaré Lemma we proved a couple of lectures
ago). So, what is left to prove is that (c) is possible, in the sense
that this "thing" does not depend on the choice of the partition, the
discs and the antiderivatives.
We first realize that if we change one of the antiderivatives in one
of the discs, ie, we replace Fj by another antiderivative
Gj in the definition of the "thing", we obtain the same
result, since Fj=Gj+D for some complex constant
D, and therefore,
Fj(s(tj))-Fj(s(tj-1))=Gj(s(tj))-Gj(s(tj-1)).
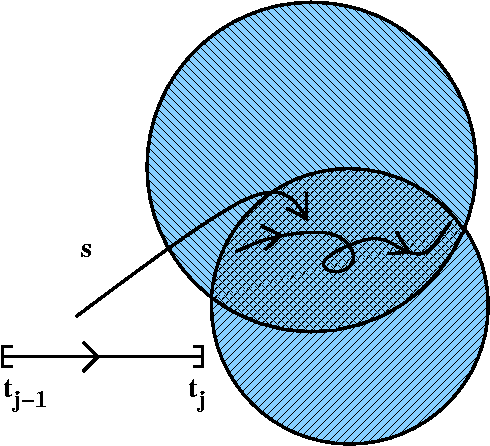 Now, if we select another disc
DRj(Zj) instead the original
Drj(zj) disc, ie, we have
s([tj-1,tj]) contained in
Drj(zj) and a antiderivative
Fj, and s([tj-1,tj]) contained in
DRj(Zj) and a antiderivative
Gj. In this situation, since both discs are open, the
intersection is a non empty, open, convex set (hence connected),
therefore we can proceed by selecting a unique antiderivative in the 2
discs (this was a HW problem). The Gj and Fj
differ by a constant, as in the previous paragraph.
Now, if we select another disc
DRj(Zj) instead the original
Drj(zj) disc, ie, we have
s([tj-1,tj]) contained in
Drj(zj) and a antiderivative
Fj, and s([tj-1,tj]) contained in
DRj(Zj) and a antiderivative
Gj. In this situation, since both discs are open, the
intersection is a non empty, open, convex set (hence connected),
therefore we can proceed by selecting a unique antiderivative in the 2
discs (this was a HW problem). The Gj and Fj
differ by a constant, as in the previous paragraph.
Finally, if we change the partition, we proceed using the Calc I
approach: we only need to prove that this "thing" does not change if
we add a new point to the partition.
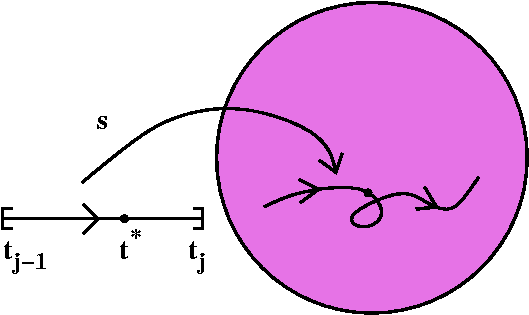 So if we add t* with
tj-<t*tj, and we select discs such
that s([tj-1,t*]) is contained in
Da(za), s([t*,tj]) is
contained in Db(zb), with antiderivatives
Fa and Fb respectively, we can prove, using the
same intersection, open, convex, connected argument used above,
that
So if we add t* with
tj-<t*tj, and we select discs such
that s([tj-1,t*]) is contained in
Da(za), s([t*,tj]) is
contained in Db(zb), with antiderivatives
Fa and Fb respectively, we can prove, using the
same intersection, open, convex, connected argument used above,
that
(Fb(s(t*))-Fb(s(tj-1)))+(Fa(s(t*))-Fa(s(tj-1)))=Fj(s(tj))-Fj(s(tj-1)). (Picture)
We have already seen that if s is a piecewise
C1 curve, the "thing" is equal to the usual value of the
integral of f(z)dz on s. Therefore we can say that this "thing"
is in fact a good definition of the integral of f over the C^0 curve
s:  sf(z)dz.
sf(z)dz.
We return to the main result of this course.
Theorem (Cauchy's Theorem) Given U a open subset of C, a
holomorphic function f in U, and two closed C0 homotopic
curves, s and r, then
 sf(z)dz=
sf(z)dz=  tf(z)dz.
tf(z)dz.
Proof Suppose H:[0,1]x[0,1]->U is the C0 homotopy
between s and t, namely H is a C0 function in [0,1]x[0,1]
and
- H(0,t)=s(t) for t in [0,1],
- H(1,t)=r(t) for t in [0,1],
- H(s,0)=H(s,1) for all s in [0,1],
We note that H([0,1]x[0,1])=K is a compact subset of U since H is
continuous. Therefore there exists a R>0 such that DR(k) is
contained in U for all k in K. Since H is uniformly continuous on
[0,1]x[0,1], there is d>0 such that if we divide [0,1]x[0,1] in
small squares Sj, so that each square has diameter less
than d, H(Sj) is contained in some DR(k).
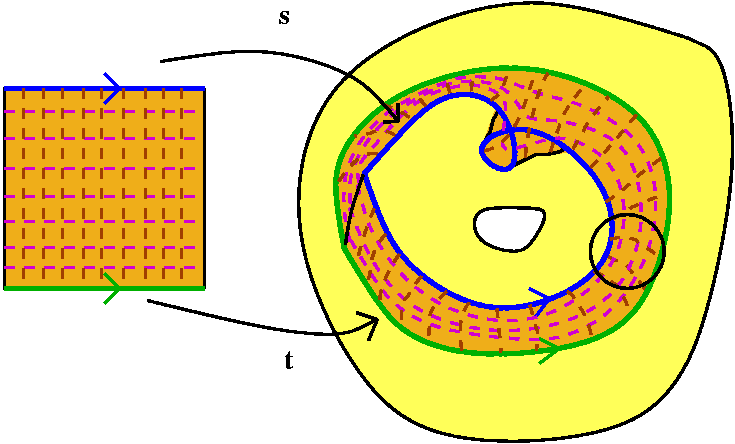 The picture to the right is supposed to show the
situation. Sigh. It is complicated. The circle shown in U, to the
right, is the boundary of a disc enclosing the image of one of the
"tiny" rectangles. Good luck in understanding the picture!
The picture to the right is supposed to show the
situation. Sigh. It is complicated. The circle shown in U, to the
right, is the boundary of a disc enclosing the image of one of the
"tiny" rectangles. Good luck in understanding the picture!
Now, we can use the "thing" formula to compute the integral of f over
the image by H of the border of Sj. From the formula we
note that that integral has to be 0, since it is over a closed curve
in a connected region and f has a holomorphic antiderivative in that
region (this is why we select the discs and the partition of the unit
square).
So if we are smart enough, we can use the fact above to prove that the
integral of f over H|{0}x_=s is equal to the
integral of f over H|{1}x_=t (It is just a big
telescopic sum together with the fact that the homotopy is also a
"closed curve", namely, the number 3 of the properties of the
homotopy).
In fact, one detail was left out, and thanks to
brave Mr. Kim, this will be discussed
in the next lecture.
Now some corollaries:
Corollary 1 If s is a closed curve which is C0
homotopic to a point in U open set, and f is a holomorphic function in
U, then the integral of f over s is equal to 0:
 sf(z)dz=0.
sf(z)dz=0.
Definition U is called simply connected if all
C0 closed curves in U are homotopic to a point in U.
Examples
- If U is convex or star shaped, then U is simply connected: For any
closed curve s, H(a,b)=az0+(1-a)s(b) is a homotopy between
s and a "curve" which is constantly z0.
- C\{0} is open and connected but NOT simply connected: The integral
of 1/z over the unit circle is not 0. Since 1/z is holomorphic in
C\{0}, this together with corollary 1 shows that the unit circle is
not homotopic to a point in C\{0}.
Corollary 2 If U is simply connected, and s is a closed curve in
U, then for any f holomorphic in U, the integral of f over s is equal
to 0:  sf(z)dz=0.
sf(z)dz=0.
Is any sort of converse true?
But we want more theorems. Here is a
Possible Theorem For U a open subset of C, s a closed
C0 curve in U, and if for every holomorphic function in U,
 sf(z)dz=0, then s is homotopic to a point. sf(z)dz=0, then s is homotopic to a point.
But this is false, since we can
provide a counterexample:
U=C\{0,1}, and suppose that s is the curve given in the picture, then
the integral of any function holomorphic in U over s is 0, but s is
not homotopic to a point (this is because U has a non trivial
fundamental group, moreover is a free group with two generators a,b,
and the s is the curve aba-1b-1.)
| 
|
The purpose of the numbers is to help you "see" the curve. The numbers
are successive positions on the curve, not values of the
parameter. Maybe you can see how a point on the curve would travel. I
would like to convince you that if f is holomorphic in C\{0,1} then
 sf(z)dz=0. sf(z)dz=0.
The first picture, to the left, shows a region inside the green
rectangle with two arrows which indicate how a homotopy would go. It
would push the curves into the x-axis at a point between 0 and
1. Because of Cauchy's Theorem, the value of the integral of a
holomorphic f around the homotopied curve won't change. In the second
picture, to the right, I hope you can "see" that the integral of f
around the curve will be 0. There are really four pieces, and if we
split the curve into those four pieces, each piece can be homotopied
into the reverse of another piece (the curve going
backwards). Therefore the integrals will all cancel.
|
|
| |
This does not prove that the curve can't be homotopied to a
point. I can't do that right now in this course, but maybe (?) this is
"clear", since we would somehow have to pull one loop over a hole in
order to untangle the curve.
This curve is homologous to 0. In fact, homology theory gives a
better language for curves and integrals of holomorphic functions --
the Cauchy Theorem has, more or less, a nice converse. For this you
need to learn a bit more, and then read a homology version of the
Cauchy Theorem (the textbook has this). I presented this homotopy
version because I think it is a bit easier to learn. The first
homology group of an open subset of C is the fundamental group mod its
commutator subgroup.
See also the classroom note by Peter Lax in the October 2007 edition
of the American Mathematical Monthly. There he describes this
situation as one of his favorite oral qualifying exam questions.
For those of you who are sophisticates, you know that C\{0,1} has a
universal covering space, and the deck transformations of that space
"are" the Fundamental Group of C\{0,1}. The mapping from the universal
covering space (which can be thought of as C!) can be realized as a
specific holomorphic function, called the
elliptic modular function. This function is very important in number
theory, and, once "constructed", can be used to give a very neat,
brief proof of a famous result called the Great Picard Theorem.
|
Now the also famous
Theorem (Cauchy Integral Formula) Given U open in C, f
holomorphic in U, and a disc Dr(p) compactly contained in
U, with the boundary curve C of Dr(p) oriented as
usual. Then for any z in Dr(p),
f(z)=(1/2Pi i)  C{f(q)/(q-z)}dq.
C{f(q)/(q-z)}dq.
 Proof Fix z, and define g(w)=f(w)/(w-z). Then g is holomorphic
in U\{z}. Next we note that C is homotopic in U-{z} to D, the boundary
of a circle of radius v centered at p (v sufficiently small -- such a
disc exists since U is open), hence by Cauchy's Theorem the integral
of g over C is equal to the integral of g over D. A
possible picture of the homotopy is to the right.
Proof Fix z, and define g(w)=f(w)/(w-z). Then g is holomorphic
in U\{z}. Next we note that C is homotopic in U-{z} to D, the boundary
of a circle of radius v centered at p (v sufficiently small -- such a
disc exists since U is open), hence by Cauchy's Theorem the integral
of g over C is equal to the integral of g over D. A
possible picture of the homotopy is to the right.
Finally, we parametrize D using q=p+veit with t in [0,2Pi].
Here is what happens: dq=veiti dt and
q-z=veit so that
 D{f(q)/(z-q)}dq=
D{f(q)/(z-q)}dq=  02Pif(z+veit)i dt.
02Pif(z+veit)i dt.
The significant thing is that the apparant
"singularity" in the bottom (the "Cauchy kernel") somehow goes away.
Even more magic (?) occurs, because the statement that f is continuous
at z is logically equivalent to f(z+veit)-->f(p)
uniformly for t in [0,2Pi]. Therefore we can exchange
limit (as v-->0) and integral to get 2Pi i f(z).
Proposition If f is holomorphic in U, then f is
C2(U) and f´ is holomorphic in U.
Proof The initial idea was to write f´ as the limit of
(f(z+h)-f(z))/h and then use Cauchy's integral formula, but the class
ended just at this point. Hopefully the proof will be completed in the
next class period.
And in closing, I think it is important to re-quote Von Neumann: "In
mathematics you don't understand things. You just get used to them"
The instructor remarked that when he finally (?)
verifies this result, one remarkable consequence will be that
C2 solutions of
 xxu+
xxu+ yyu=0 will turn out to
be C
yyu=0 will turn out to
be C . This is not at all an obvious fact.
. This is not at all an obvious fact.
Historically, the Laplacian was one of the oldest partial differential
operators studied because of its importance in physical modeling. I
think an even earlier example of a partial differential operator was
this:  xx-
xx- yy (note the very important difference in
sign!). Solutions of the homogeneous equation corresponding to this
operator (solutions of "the wave equation") are of the form
f(x+y)+g(x-y) where f and g are any C2 functions of
one variable. You can check this easier using the Chain Rule. However,
these solutions do not need to be C
yy (note the very important difference in
sign!). Solutions of the homogeneous equation corresponding to this
operator (solutions of "the wave equation") are of the form
f(x+y)+g(x-y) where f and g are any C2 functions of
one variable. You can check this easier using the Chain Rule. However,
these solutions do not need to be C (this involves
what are called "shocks").
(this involves
what are called "shocks").
So the change from + to - is significant, and that harmonic functions
must be C is not at all obvious!
is not at all obvious!
| Friday,
September 21 | (Lecture #6) |
|---|
Notes by Susan Durst, edited, with
some comments by the instructor.
Today we began by computing some line integrals in order to examine some
possible truths.
Possible Truth #1 The line integral of any continuous
function on any closed curve is 0. (This would be
very interesting if it
were true and would make much of physics and mathematics
unnecessary.)
Counterexample #1 f(z)=1+2z+z(z-bar) integrated clockwise
around s, the border of the upper right quadrant of the circle
centered at 0 of radius 2.
We broke the path sigma into three segments s1,
s2, and s3. s1 was the line segment
from 0 to 2. s2 was the circular arc from 2 up to 2i.
s3 was the line segment from 2i to 0.
We know that  sf(z)dz=
sf(z)dz= s1f(z)dz+
s1f(z)dz+ s2f(z)dz+
s2f(z)dz+ s3f(z)dz.
s3f(z)dz.
 s1f(z)dz=
s1f(z)dz= 021+2t+t2dt=t+t2+t3/3]02=2+4+8/3.
021+2t+t2dt=t+t2+t3/3]02=2+4+8/3.
 s2f(z)dz=
s2f(z)dz= 0Pi/2(1+4eit+4)2ieitdt=2i
0Pi/2(1+4eit+4)2ieitdt=2i
 0Pi/24e2it+5eitdt=2i((4/(2i))e2it+(5/i)eit)]0Pi/2=(-4+10i)-(4+10)=-18+10i.
0Pi/24e2it+5eitdt=2i((4/(2i))e2it+(5/i)eit)]0Pi/2=(-4+10i)-(4+10)=-18+10i.
 s3f(z)dz=-
s3f(z)dz=- 02(1+2it+t2)i dt=-i(t+it2+t3/3)]02=-i(2+4i+8/3)
02(1+2it+t2)i dt=-i(t+it2+t3/3)]02=-i(2+4i+8/3)
It is important to notice the way that each of the parametrizations of
the curves was chosen. The first straight line segment was given by t
on the interval [0,2]. The curve was given by 2eit on the
interval [0,Pi/2]. The third was given by i t on the interval
[0,2]. We needed to multiply the integral by -1 so that we were
integrating the line segment from 2i to 0 rather than the line segment
from 0 to 2i.
All this gives us  sigma f(z)dz =
2+4+8/3-18+10i-i(2+4i+8/3).
This is not equal to zero, so Possible Truth #1 is false.
sigma f(z)dz =
2+4+8/3-18+10i-i(2+4i+8/3).
This is not equal to zero, so Possible Truth #1 is false.
Possible Truth #2 The line integral of any holomorphic function
over any closed curve is zero.
Counterexample #2 f(z)=1/z, integrated counterclockwise around
s, the unit circle.
 sf(z)dz=
sf(z)dz= 02Pie-itieitdt=
02Pie-itieitdt= 02Pii dt=2iPi.
02Pii dt=2iPi.
This is not equal to zero, so Possible Truth #2 is false.
Possible Truth #3 The line integral of any holomorphic function
with a singularity inside a closed curve is not zero.
Counterexample #3 (Note: z2/z works (!) but maybe that singularity isn't too bad ...)
f(z)=1/z2, integrated counterclockwise around s, the unit
circle.
 sf(z)dz=
sf(z)dz= 0Pie-2itie2itdt=ie-it/-i]02Pi=0.
0Pie-2itie2itdt=ie-it/-i]02Pi=0.
Note that this
last step works because exp is 2Pi i periodic (or you can just
evaluate the exponentials!) Possible Truth
#3 is false.
We then resumed our discussion of Cauchy's Theorem.
Cauchy's Theorem If U is open in C, and s and t are closed
curves in U with s homotopic to t in U and f holomorphic in U, then
 sf(z)dz=
sf(z)dz= tf(z)dz.
tf(z)dz.
Corollary If U is open in C and f is holomorphic in U, then if
s is a closed curve which is homotopic to a point (some constant
function t) then  sf(z)dz=0.
sf(z)dz=0.
We proceeded to talk about the kind of proofs which are often given in
other settings.
Proof 1 Would I lie to you?
Proof 2 If you move the path just a little bit, the difference
between the integral of the old path and the integral of the new path
will be really small, so we can assume it's equal to zero. See below.
Proof 3 Proof via Green's theorem: If s is the boundary of a
region R oriented positively, so the region R is to
the left as the parameter value increases, then  sf(z)dz=2i
sf(z)dz=2i
 Rdf/d(z-bar)dxdy. If the function is holomorphic,
then df/d(z-bar) is zero, so
Rdf/d(z-bar)dxdy. If the function is holomorphic,
then df/d(z-bar) is zero, so  f(z)dz=0.
f(z)dz=0.
The problems with proofs 1 and 2 are relatively clear. Proof 3 looks
nicer, but it causes problems when you're dealing with really tangled
curves, and it involves actually proving Green's theorem, which in all but
a few cases is just as difficult as proving Cauchy's theorem.
Proof 4 Use Simplicial Approximation. Essentially, a curve s
can be approximated by a polygonal curve p such that  sf(z)dz=
sf(z)dz= pf(z)dz for all holomorphic
functions f. (This is a problem late in chapter 2 of the text.) And
approximate the homotopy similarly by a collection of polygonal
mappings over, say, triangles. With a finite collection of polygons
and line segements, we could prove Cauchy's Theorem piece by piece.
pf(z)dz for all holomorphic
functions f. (This is a problem late in chapter 2 of the text.) And
approximate the homotopy similarly by a collection of polygonal
mappings over, say, triangles. With a finite collection of polygons
and line segements, we could prove Cauchy's Theorem piece by piece.
Simplicial approximation is one of the classical
methods used in algebraic topology since about the 1930's.
Proof 5 Piecewise continuous curves can be similarly
approximated using smooth (C ) curves.
) curves.
So one can sort of turn algebraic topology into
differential topology. This is done in some detail in Peter Lax's
article on the Cauchy integral (American Mathematical Monthly, October
2007).
Now that we have seen these, we will proceed to prove Cauchy's theorem in
an entirely different way.
Recall the Lebesgue Number Theorem If K is a compact metric
space and {Ua}, a in A, is an open cover of K, then there
exists a Lebesgue number d>0 such that for any k in K, there exists a
in A such that Bd(k) is in Ualpha.
More elaborately and less understandably stated, the
covering of K by balls of radius d is subordinate to the
covering by the Ua's.
Corollary Suppose U is open in C, and K is compact in U. Then
there exists compact set L such that K is in the interior or L, and L is
contained in U.
This will be needed later in the course.
Proof Since U is open, we know that for every k in K, there
exists r_k>0 such that Brk(k) is contained in
U. So {Brk(k)}k in K is an
open cover of K, so it has a Lebesgue number d. Take L to be the
union over all k in K of the closure of Bd/2(k).
Professor Greenfield left the proof to the students. It goes something
like this:
Every k in K is contained in Bd/4(k), which is an open ball
entirely contained in the closure of Bd/2(k), which is
contained in L. Therefore every point in K is an interior point of L.
Thus K is contained in the interior of L. etc., etc.
but I don't know whether he wants it included in the notes for the day.
Recall the definition of uniform continuity: If X and Y are metric
spaces, then f is a uniformly continuous function from X to Y if for
any e>0, there exists a r>0 such that if x1 and
x2 are in X and
dX(x1,x2)<r, then
dY(f(x1),f(x2)<e.
Proposition If K is a compact metric space, Y is another metric
space, and f is a continuous function from K to Y, then f is uniformly
continuous.
Proof Let e>0. Look at Be/2(y) for y in Y.
f-1(Be/2(y)) is open in K since f is
continuous. Therefore
{f-1(Be/2(y))}y in Y is an
open cover of K. So it has a Lebesgue number de. Suppose
dK(k1,k2)<de. Then
k1and k2 are in the same ball of radius
de. This ball is contained in
f-1(Be/2(y)) for some y in Y. So
f(k1) and f(k2) are both in Be/2(y).
Therefore
dY(f(k1)-f(k2))<=dY(f(k1),y)+dY(f(k2),y)<e/2+e/2=e.
So f must be uniformly continuous.
DIGRESSION
We then had a short digression on uniform continuity, following an even
shorter digression on the word digression and its translation into
Chinese. ’Î¥’Âê
We came up with the following examples and
verification of the stated properties of these examples is
clear (?):
- A function from R to R which is continuous but not uniformly
continuous: f(x)=x2.
- A function from R to R which is continuous and bounded, but not
uniformly continuous: f(x)=sin(x2).
Note that the derivative in this instance is not bounded.
- Theorem If f is a function from R to R which is
C1 and the derivative is bounded, then f is uniformly
continuous.
Possible Result If f is a function from R to R which is
piecewise C1 and uniformly continuous, then the derivative
of f is bounded.
This turns out to be false.
- A piecewise C1 function which is uniformly continuous
and which has unbounded derivative: one example is
f(x)=x1/3, and another is a series of very steep but very
short tents.
About the tents
Useful examples can be made with just piecewise linear
functions. Imagine a "tent" as shown to the right, centered at the
positive integer, n. The important dimensions are an, the
height at n, and bn, the distance to the bottom of the tent
from either side of the center at n. In this case, suppose
an=1/10n (very short!) and
bn=1/(n·10n). Then the slopes of the tent
sides are +/-n, which certainly grow large. But the height of the tent
is so small that the function, even though it locally may have a huge
derivative, can never grow very big. This function is uniformly
continuous on R if there's such a (varying!) tent at each positive
integer.
With more effort, a very smooth function can be specified which looks
a great deal like the tents, but with the corners made smoother.
tent in Romanian is (maybe!) cort. I think I should give
up on this, because almost surely I will say or write something wrong
or improper.
| 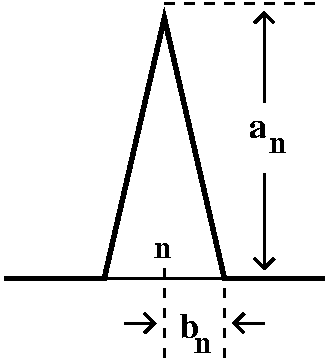 |
Boxes and butterflies
Suppose we "look" at a graph of a function on R, say. When is it
uniformly continuous? Well, "Given e>0, there must exist
..." but what about the picture? If (x,f(x)) is on the graph, and if a
positive (vertical!) epsilon is given, we should be able to get
a positive (horizontal!) delta so that centering a box at (x,f(x)) traps (?) the graph above (x-delta,x+delta) entirely inside the box.
To the right is shown two pictures of the same graph, a continuous
function on a closed interval, hence uniformly continuous. The blue box on the left is an attempt to select a delta
in response to the epsilon given. For much of the curve shown, this
delta is satisfactory. For example, the blue shadow box centered on a
point on the graph to the left shows the curve correctly "trapped" in
the box, and escaping as desired from from the sides. However, the
curve is steeper at the right-hand point on the curve. When we
consider the blue shadow box there, the curve escapes from the
top. The epsilon inequality is not satisfied for the delta given.
| 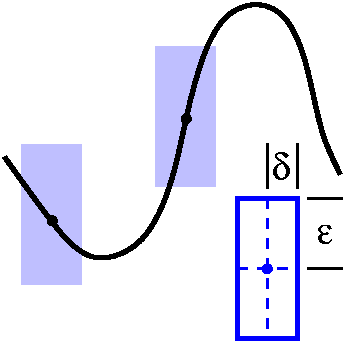
|
|
We can fix this with a smaller choice of the horizontal dimension,
operating in the domain space. In this green
box picture, that smaller choice allows the green shadow box, centered
on a point on the previously troublesome steep part of the curve, to
hold the curve inside and have it escape the vertical sides.
Uniform continuity asserts that given a vertical dimension,
there is some horizontal dimension so that if a congruent box
is centered at each point of the curve, the part of the curve which is
contained in the box will escape through the vertical sides.
| 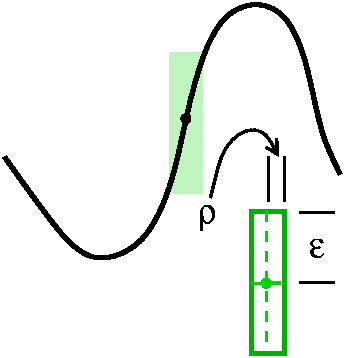 |
|
A function satisfies a uniform Lipschitz condition if there is
K>0 so that
|f(x1)-f(x2|<=K|x1-x2|. The
graph drawn is fairly smooth, and is presumably C1. If such
a function also has a bounded derivative, then the function satisfies
a uniform Lipschitz condition (this is implied by the Mean Value
Theorem). This is more delicate, and indicates that a butterfly (!!)
centered at each point of the graph would enclose the graph within its
wings. Butterflies can be put into boxes, so functions satisfying
uniform Lipschitz conditions are uniformly continuous.
But boxes can't be put inside butterflies. More comprehensibly,
sqrt(x) is uniformly continuous on [0,1] since it is continuous on a
compact set. But it does not satisfy a Lipschitz condition at 0: Take
x1 to be 0 in
|f(x1)-f(x2|<=K|x1-x2|
and get sqrt(x2)<=Kx2 for all
x2>0. This means 1<=Ksqrt(x2) for such
x2's (such as 1/{2K}), which is false for any K. Square
root has no butterflies at 0.
| 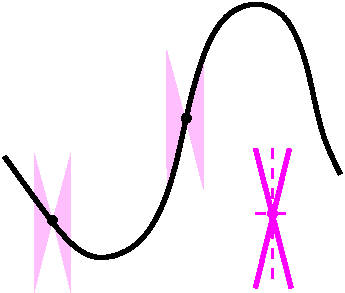 | |
END OF DIGRESSION
Suppose s is a continuous function from [a,b] to an open set U in C.
Claim There exists a partition of [a,b]:
a=t0<t1<...<tn-1<tn=b
and open discs Drj(zj) in U for
1<=j<=n such that for any j in {1,2,...,n},
s([j-1,tj]) is contained in
Drj(zj).
Proof Let K=s([a,b]). U is open, so for k in K, there exists
e_k such that Dek(k) is in U. Therefore
{Dek(k)|k in K} is an open cover of K. Since
the continuous image of a compact set is compact, K is compact.
Therefore, there exists a Lebesgue number r for our open cover. f is
uniformly continuous. So there exists a d>0 such that if
[s1,s2] is in [a,b] and
s2-s1
We can take an antiderivative Fj in each
Drj(zj). This proof will be finished
in the next class period.I hope.
| Tuesday,
September 18 | (Lecture #5) |
|---|
Notes by Brandon Bate, edited, with
some comments by the instructor.
Last class, we assumed that g=f´/f is C1 so as
to find an anti-derivative for g. However, we assumed that
f was only C1, which implies that g is C0. We
cannot guarantee g has an antiderivative in this case.
Professor Greenfield assured the class that g was in fact
C1 and that this result would be proved in two weeks.
But can we trust Professor
Greenfield? Perhaps he will deceive us with a wrong use of the Axiom
of Choice ...
We defined
 ab
f(t) dt =
ab
f(t) dt =  ab g(t) dt + i
ab g(t) dt + i  ab h(t) dt
where f:[a,b]--> C is continuous and f(t) = g(t) + i h(t). We then
proved the following proposition.
ab h(t) dt
where f:[a,b]--> C is continuous and f(t) = g(t) + i h(t). We then
proved the following proposition.
Proposition: | ab f(t) dt|<=
ab f(t) dt|<= ab|f(t)|dt
ab|f(t)|dt
Proof: If the integral is 0, the result is correct. Define h = [ ab f(t) dt)/|
ab f(t) dt)/| ab f(t) dt|].
Observe
that h is in C and |h|=1. We now perform the following sneaky
calculation:
ab f(t) dt|].
Observe
that h is in C and |h|=1. We now perform the following sneaky
calculation:
| ab f(t)
dt|= h-1
ab f(t)
dt|= h-1 ab f(t) dt =
ab f(t) dt =  ab
h-1 f(t) dt = Re
ab
h-1 f(t) dt = Re  ab h-1 f(t) dt =
ab h-1 f(t) dt =  ab Re( h-1 f(t) ) dt.
Since Re(w)<=|w| for all w in C we conclude that
|
ab Re( h-1 f(t) ) dt.
Since Re(w)<=|w| for all w in C we conclude that
| ab f(t)
dt| =
ab f(t)
dt| = ab Re(
h-1 f(t) ) dt <=
ab Re(
h-1 f(t) ) dt <= ab|h-1 f(t)| dt =
ab|h-1 f(t)| dt =  ab|f(t)|dt.
ab|f(t)|dt.
We then defined some terms. We said that s:[a,b]-->C is a
C1 curve if s(t) =s1(t) + i s2(t) and
s1, s2 are C1. Next we defined  sf(z)dz=
sf(z)dz= abf(s(t))s´(t)dt where f is
continuous in an open subset U of C and s is a C1 curve
with s([a,b]) contained in U.
abf(s(t))s´(t)dt where f is
continuous in an open subset U of C and s is a C1 curve
with s([a,b]) contained in U.
With these definitions we proved the following theorem:
Theorem 1:
If F is holomorphic in U, F´=f, and s is a C1 curve in U
then  s f(z) dz = F(s(b))-F(s(a)).
s f(z) dz = F(s(b))-F(s(a)).
Proof: Notice  s
f(z)dz =
s
f(z)dz =  ab
f(s(t))s´(t) dt =
ab
f(s(t))s´(t) dt =  ab F´(s(t))s&180;(t) dt =
ab F´(s(t))s&180;(t) dt =  ab d/dt(F(s(t))
dt = F(s(b))-F(s(a)).
ab d/dt(F(s(t))
dt = F(s(b))-F(s(a)).
We also stated the following theorem. The proof is left as a homework
problem since the instructor can't do it in public.
Theorem 2:
(Reparameterization - Prop 2.1.9) Let s:[a,b]-->U be a C1 curve,
f continuous on U, and y:[c,d]-->[a,b] a one-to-one C1
function with y(c)=a and y(d)=b. If t=s composed with y then
 tf(z)dz =
tf(z)dz =
 sf(z)dz.
sf(z)dz.
Theorem 2 shows that the parameterization of a curve doesn't matter
when evaluating the integral.
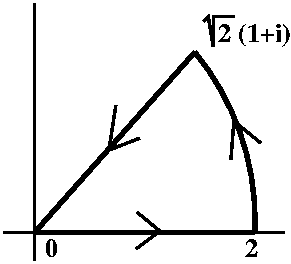 EXAMPLE (I should have provided an example before
going on!) Let's consider the closed curve shown, a line segment from
0 to 2, then a quarter circle for 1 to sqrt(2)(1+i), followed by a
line segment from sqrt(2)(1+i) to 0. (Notice that |sqrt(2)(1+i)|=2.)
I'll call this curve s. This is certainly a piecewise C1
curve. I will just choose a polynomial of low degree in z and z-bar,
since I am lazy. So suppose f(z)=1+2z+z(z-bar), a quadratic
polynomial. Let's compute
EXAMPLE (I should have provided an example before
going on!) Let's consider the closed curve shown, a line segment from
0 to 2, then a quarter circle for 1 to sqrt(2)(1+i), followed by a
line segment from sqrt(2)(1+i) to 0. (Notice that |sqrt(2)(1+i)|=2.)
I'll call this curve s. This is certainly a piecewise C1
curve. I will just choose a polynomial of low degree in z and z-bar,
since I am lazy. So suppose f(z)=1+2z+z(z-bar), a quadratic
polynomial. Let's compute  sf(z)dz.
sf(z)dz.
s is the sum (the concatenation!) of
s1+s2+s3, where s1 and
s3 are line segments and s2 is a circular arc.
- Computing the integral over s1: parameterize by just
the function t, with t in [0,2]. Then the recipe
 abf(s(t))s´(t)dt becomes:
abf(s(t))s´(t)dt becomes:
1+2z+z(z-bar)-->1+t+t2
s´(t)dt-->dt
and we compute  011+t+t2dt=t+(1/2)t2+(1/3)t3]01=1+(1/2)+(1/3)=(11/6).
011+t+t2dt=t+(1/2)t2+(1/3)t3]01=1+(1/2)+(1/3)=(11/6).
- Computing the integral over s2: parameterize by the
function 2eit, with t in [0,Pi/4]: this is a complex
analysis course, and I will almost always parameterize circular arcs
with exp! Then the recipe
 abf(s(t))s´(t)dt becomes:
abf(s(t))s´(t)dt becomes:
1+2z+z(z-bar)-->1+4eit+4
s´(t)dt-->i2eitdt
and we compute  0Pi/4(1+4eit+4)i2eitdt
0Pi/4(1+4eit+4)i2eitdt
 0Pi/42ieit+8ie2it+8ieitdt
=2eit+4e2it+8eit]0Pi/4=
((2(1+i)/sqrt(2))+4i+8(1+i)/sqrt(2)(-
(2+4+8)=5sqrt(2)(1+i)+4i-14.
0Pi/42ieit+8ie2it+8ieitdt
=2eit+4e2it+8eit]0Pi/4=
((2(1+i)/sqrt(2))+4i+8(1+i)/sqrt(2)(-
(2+4+8)=5sqrt(2)(1+i)+4i-14.
- Computing the integral over s3: well, the line segment
will be t-->eiPi/4t for t in [0,2], but I need to reverse
it, because the end of the segment should be the origin. So I must put
in an additional -.
1+2z+z(z-bar)-->1+2eiPi/4t+4t2
s´(t)dt-->eiPi/4dt
Now compute - 02(1+2eiPi/4t+4t2)eiPi/4dt. This
is -eiPi/4(t+eiPi/4t2+(4/3)t3)]02. Wow! There's nothing
at 0, and the value at the top is -eiPi/4(2+eiPi/4+(32/3)) which is
-sqrt(2)(1+i)-i-(16sqrt(2))/3.
02(1+2eiPi/4t+4t2)eiPi/4dt. This
is -eiPi/4(t+eiPi/4t2+(4/3)t3)]02. Wow! There's nothing
at 0, and the value at the top is -eiPi/4(2+eiPi/4+(32/3)) which is
-sqrt(2)(1+i)-i-(16sqrt(2))/3.
So the value of the integral over this closed curve is:
(11/6)+5sqrt(2)(1+i)+4i-14-sqrt(2)(1+i)-i-(16sqrt(2))/3
Is this equal to 0?
Next we defined concatenation of curves. Suppose s:[a,b]-->C and
t:[c,d]-->C are C0 s(b)=t(c). We then define
(s+t)(t)=s(t)
if a<=t<=b and s+t(t) = t(t-b+c) if b<=t<=b+d-c. So s+t is
a curve whose domain is [a,b+d-c],
We say that a curve is piecewise C1 if it the finite sum of
C1 curves.
Next we made a provisional definition for the integral over a
piecewise C1 curve. If s=s1+...+sn
where sj is C1 for 1<=j<=n then we define
 sf(z)dz to be
sf(z)dz to be  s1f(z)dz+...+
s1f(z)dz+...+ snf(z)dz. The
difficulty with this definition is that s may be expressed as two
different sums of C1 curves. For instance, we may have
s=s1+s2 and s=t1+t2 with
no simple relationship between the pieces individually. In order for
our definition of the integral to make sense need the following Lemma.
snf(z)dz. The
difficulty with this definition is that s may be expressed as two
different sums of C1 curves. For instance, we may have
s=s1+s2 and s=t1+t2 with
no simple relationship between the pieces individually. In order for
our definition of the integral to make sense need the following Lemma.
Lemma:
If s=s1+..+sn
and s=t1+..+tm
then
 s1f(z)dz+...+
s1f(z)dz+...+ snf(z)dz is equal to
snf(z)dz is equal to
 t1f(z)dz+...+
t1f(z)dz+...+ tmf(z)dz.
tmf(z)dz.
Proof Idea:
This proof uses partitions from Calculus 1. Observe that it is
possible to find a partition
a=t0<t1<...<tn=b so that
s|[tj-1,tj] = sj.
Likewise, there is a partition
a=t*0<t*1<...<t*m=b so that
s|[t*k1,t*k]=tk. One
needs only to take the refinement of these partitions to see that the
Lemma is true. And the refinement can be done by just adding one point
to a given partition and proving equality of the resulting sum of
integrals. Then both of the partitions given have a common refinement,
obtained by taking their union. This common refinement can be gotten
by including one more point a finite number of tiems.
After proving this lemma we discussed whether the prior theorems would
also hold for piecewise curves. The first theorem holds due to the
fact that the integral of a piecewise curve is a telescoping sum. The
second theorem might be true. (Think about piecewise C1
change of parameters.) We also defined -s:[a,b]--.C to be
(-s)(t)=s(b+a-t) for s:[a,b]-->C, a C0 curve. We noted that
 -sf(z)dz=-
-sf(z)dz=- s f(z)dz if f is
C0 and s is piecewise C1.
s f(z)dz if f is
C0 and s is piecewise C1.
A C0 curve is closed if its start is the same as its
end: s:[a,b]-->C with s(a)=s(b).
We discussed what it meant for two closed C0 curves
s:[0,1]-->C and t:[0,1]-->C
to be homotopic. We say that s is homotopic to t in U,
written as s~t in U if there is a
C0 mapping H:[0,1]x[0,1]-->U so that:
- H(0,t)=s(t) for t in [0,1].
- H(1,t)=t(t) for t in [0,1].
- H(s,0)=H(s,1) for all s in [0,1].
H is called a homotopy between s and t.
We need the third requirement in the
definition, otherwise detecting holes in domains (connected open sets)
will be impossible with homotopies. Look at the picture below, which
is supposed to be "snapshots" (?) of a fake homotopy, without the
third requirement. We have a nice, continuous closed curve surrounding
a hole in the first, leftmost picture. We then continuously deform the
curve, now no longer closed, so it moves into a point. Hey: all
continuous curves can be deformed continuously into a point if we
don't have the third requirement.

With this definition of homotopic we stated a version of Cauchy's Theorem.
Theorem:
Suppose U is open in C. Suppose f is holomorphic on U. Suppose s and t are
piecewise C1 closed curves in U, and suppose s~t in U.
Then
 sf(z)dz=
sf(z)dz= tf(z)dz.
tf(z)dz.
Since there is supposed to be a homotopy H(s,t) between
t=H(0,t) and s=H(1,t), perhaps we should try to study the function
s--> H(s,_)f(z)dz.
This is certainly natural. One technical problem is that we don't know
how to define integration over the intermediate curves, H(s,_), which
are only supposed to be continuous. In fact, I don't know how to
define integration in general over these curves, but I can show you a
way to define integration if the integrand, f, is assumed to be
holomorphic.
H(s,_)f(z)dz.
This is certainly natural. One technical problem is that we don't know
how to define integration over the intermediate curves, H(s,_), which
are only supposed to be continuous. In fact, I don't know how to
define integration in general over these curves, but I can show you a
way to define integration if the integrand, f, is assumed to be
holomorphic.
I noted in class that the integration I was proposing to define would
not allow us to compute length of an average continuous curve (!)
because of this restriction on the integrand.
Next we began discussing how to define  sf(z)dz where s:[a,b]-->U is a
C0 curve, U is open, and f:U-->C is holomorphic. Since the
image of s is compact we are able to form a partition
a=t0<t1<...<tn=b so that the
image of each interval [tj-1,tj] fits inside a
disk Dj contained in U. Since there is Fj such
that Fj´=f in Dj then we can define
sf(z)dz where s:[a,b]-->U is a
C0 curve, U is open, and f:U-->C is holomorphic. Since the
image of s is compact we are able to form a partition
a=t0<t1<...<tn=b so that the
image of each interval [tj-1,tj] fits inside a
disk Dj contained in U. Since there is Fj such
that Fj´=f in Dj then we can define  s|[tj-1,tj]f(z)dz=Fj(s(tj))-Fj(s(tj-1)).
s|[tj-1,tj]f(z)dz=Fj(s(tj))-Fj(s(tj-1)).
There are many details to check!
With the intent to prove Cauchy's Theorem we then proved the Lebesgue
Number Lemma.
Lemma:
Suppose K is a compact metric space and {Ua}a in
A is an open cover of K
(this means each Ua is open and that the union of the Ua's is all of K).
Then there exists a d>0 so
that for all k in K, there exists a in A so that Bd(k)={x
in K | d(x,k)<d} (the open ball of radius d and center k) is
contained in Ua.
Proof: We use proof by contradiction. Suppose that the result
is false. Then for all d>0, there is a kd in K so that
Bd(kd) is not a subset of Ua,
for all a in A. Well, to me, this is, if not the
core of the proof, the principal pedagogical reason to present this
particular proof: we should all be able to negate a complicated (?)
three-layered quantified statement. Can you do such a
negation?
We can then form a sequence {kn} of K so that
B1/n(kn) not a subset of Ua
for all a in A. Since K is compact there is a subsequence
{knj} that converges to a point k* in
K. But k* must be in one of the Ua's, since we
have an open cover of K.So there is a0 in A with
k* in Ua0. Since
Ua0 is open then there is e>0 such that
Be(k*) is contained in
Ua0. Since
knj-->k*,
there is N>0 such that if j>= N then
d(knj,k*)<e/2.
Recall that B1/nj(knj) is not a
subset of Ua, for all a in A. Thus
B1/nj(knj) is not a subset of
Ua0. If we pick j0>N with
also 1/j0<e/2
then we obtain a contradiction, for we have that
B1/n(j0) is a subset of
Be(k*) which is contained in
Ua0. Use the triangle
inequality.
The Wikipedia
proof of this famous lemma is more direct, and avoids argument by
contradiction which some people dislike. I think that proof resembles
what Mr. Pal was suggesting, but I
find the proof too elaborate, almost artificial. The Lebesgue number
is a basic metric space topological idea, and I prefer proofs that I
find simple.
Possibly relevant Latin quote and a possible translation:
De gustibus non est disputandum. There's no accounting for taste.
| Friday,
September 14 | (Lecture #4) |
|---|
Notes by Avital Oliver, edited, with
some comments by the instructor.
We started with a digression to fully understand the chain rule for
complex functions. In R2 calculus we find a horrible chain
rule with matrices (Jacobian aka that matrix whose determinant is the
Jacobian). Amazingly, simply manipulating the R2 chain
rule and understanding it in the context of complex functions (and
utilizing the Cauchy-Riemann equations) turns it into the "regular"
one for R: (fg)´ = f´(g)·g´ (complex
multiplication). We like this very much.
Well, the Chain Rule in R2 is a
special case of, say, the Chain Rule in normed vector spaces. It is
actually very nice. It states that the linear approximation to a
composition is the composition of the linear approximations of the
original functions. I disagree with the word, "horrible".
Back to our propositions -- During the last lesson, we proved
propositions 1 and 2 using Poincaré's Lemma, but we didn't
really appreciate the lemma enough because we didn't understand how
much it would be difficult to prove these propositions without using
it.
Before proving proposition 3, we give a definition: If V is an open
set in C, then O(V) is the collection of holomorphic functions from V
to C. So proposition 3 is now stated as: If U is the unit disc, and f
in O(U) never vanishes then f has a logarithm in O(U) and this means there exists F in O(U) so that
eF=f. To amuse us all, the instructor gave us a
corollary of this proposition: The unit group of O(U) is
divisible. After some explanations, we were explained that "Algebra is
a worthless swamp" Please delete. The instructor's
mathematical taste is dubious.-- this corollary is just
equivalent to saying that we can take roots (square, cube, ...) of
non-vanishing holomorphic functions in the unit disc. We can prove
this easily using proposition 3 by taking the logarithm, dividing,
and plugging back into the exponential function [in the language of
"Mathematics": f^(1/n) = e^((1/n) log f)].
Now we're ready to try proving the proposition. We first try without
Poincaré's lemma:
"Proof 1"
We defined complex logarithms in an early (first?) lesson (but this is
not in the diary notes...). Just compose the logarithm. This doesn't
work because the logarithm is different for different areas of C\{0} and
there is no simple way to patch them up to create one logarithm for
the whole function (this is actually the covering homotopy property we
all love from algebraic topology. It's quite difficult to prove it
over "there", and it's just as difficult "here").
"Proof 2"
Take the power series for log. Of course, this proof has the exact
same flaw as the previous one. You can't create one power series for
log that covers "enough" of C\{0}.
Our Proof
If eF=f then F´ should be f´/f. Define
g=f´/f. Then g is in O(U) (here we use the fact
that f is non-vanishing). By proposition 2 (which is proven
using Poincaré's lemma) there is an anti-derivative to g. Let G
be this anti-derivative. All that is left is to find the right
constant to add to G, which is done easily. Wow, that was so simple
and nice.
We now move on to understanding what integrals over closed curves are
in C. We start with a small example motivated by our previous
discussion (last lesson) about finding the anti-derivative of a
holomorphic function -- if f is in O(U) then any integral on a
rectangle of f is equal to 0. We prove this using Green's theorem and
the Cauchy-Riemann equations. But what if U is not the unit circle?
Then this is sometimes true and sometimes not. This is a very large
and interesting issue and we will understand it better as the course
progresses. But we should first define what a curve is. Old-fashioned
people (like Ahlfors and Hille, our instructor's
great-great-grandfather) define rectifiable continuous curves, which
are not fun to work with. Well, many people would
disagree with the "not fun" phrase. They would assert that such curves
are actually the correct collection! Fortunately for us, our
instructor is nice enough to allow us to work with piecewise
C1 curves. We are relieved.
I mentioned the effort to develop "complex analysis"
without line integrals. Here is a reference: Topological
analysis by G. T. Whyburn. QA611.W497 1964
We finished off with a brief description of Cauchy's theorem: Let D be
a connected open set and f in O(D). Let Gamma be a piecewise C^1
closed curve which is homotopic to a point (we will discuss this in
the next lesson) then the integral of f over Gamma is 0.
We thanked the instructor and left class happily.
| Tuesday,
September 11 | (Lecture #3) |
|---|
The standard proof of the Cauchy-Schwarz inequality was given
(positive definite inner product, f(t)=(v+tw,v+tw), expand, consider
the discriminant of a non-negative real quadratic). Then some remarks
were made about how a positive definite inner product was used to
"make" a norm, and this was in turn used to give a metric on the
vector space.
The instructor mentioned his
professional ancestors.
We then discussed the Poincaré Lemma. Well, Google has more than 900,000 links for this
topic. Our version is a key local observation in the differential
calculs of R2. In the open unit disc with f and g
C1 in the disc, there is F with Fx=f and
Fy=g when fx=gy (the "compatibility
condition" for this overdetermined system of linear partial
differential equations). The proof used the Fundamental Theorem of
Calculus and differentiation under the integral.
How unique is such an F? This led to brief mention of connectedness,
pathwise or arc connectedness, and connectedness using just
concatenated horizontal and vertical line segments. F is unique up to
an additive constant.
Then the instructor attempted (started?) to verify the following three
corollaries of the Key Local Observation:
- Every harmonic function in the disc has a harmonic conjugate.
Well, we needed to define "harmonic function": h so that
hxx+hyy=0. Occuring in heat distribution as a
model of steady-state heat distribution on a thin homogeneous metal
plate. We briefly considered harmonic polynomials. If u+i v is
holomorphic with u and v being C2 (it will turn out that
the number of derivatives doesn't matter!) then both u and v are
harmonic (a consequence of the CR equations). v is called a "harmonic
conjugate" of u (but -u is a harmonic conjugate of v, sigh). We did
prove this. There are harmonic functions in the punctured plane (all
of C except the origin) which don't have harmonic conjugates.
- Every holomorphic function in the disc has an antiderivative. A
homework problem gives an example of a domain and a holomorphic
function which doesn't have an antiderivative in the domain. A bit
more needs to be said about this.
- Every non-vanishing holomorphic function in the disc has a
logarithm. This must be investigated.
| Friday,
September 7 | (Lecture #2) |
|---|
We discussed the equivalence of the text's definition of "u+iv
is holomorphic" (C1 and annihilated by d/dz-bar) with the
existence of the limit of a complex difference quotient. Also
mentioned was Goursat's result that if that limit exists, then
assumption of the existence of the limit was sufficient. We got
formulas for the derivative, f´(z) of a holomorphic function f(z).
I stated the Loomen-Menchoff Theorem: if the x and y derivatives of u
and v all exist in some open set, and if these derivatives satisfy the
CR equations, then u+iv is holomorphic. The proof of this
relies on delicate measure-theoretic arguments, and the best reference
I have is 6 pages in Narasimhan's book (see the text references,
please).
Since both d/dz and d/dz-bar are pure first order PDE's, the sum,
product, quotient (where defined), and composition of holomorphic
functions is holomorphic, and the formulas for the derivatives are the
familiar ones.
Then we discussed Euler's formula. For that we needed to digress and
define the exponential function, which I did according to the text. I
also stated this was the only reasonable definition. Here's a fact:
there is a unique solution to the following PDE problem:
u and v
are C1 in C, they satisfy the CR equations in
C, and u(x,0)=ex (the calculus exponential) and
v(x,0)=0. This is not totally obvious. The text supplies one solution
but why couldn't there be others?
The text's solution to what is ez is a homomorphism of the
additive group of C to the multiplicative group of C. We
also obtained formulas for the inverse, maybe called log. This
function has some problems. First, exp is 2Pii periodic, so
there are many logs. Second, I described how to define log explicitly
in the right half-plane (there are similar formulas in the left and
upper and lower half-planes). But there is no valid formula in all of
C\{0}. What is arg? This log is holomorphic, and its derivative
(we checked this in the right half-plane) is 1/z.
We very briefly discussed the group of roots of unity, an interesting
group, and how it looks sitting in the unit circle |z|=1.
Then we finally proved: if zj-->z then
|zj|-->|z|. We did this by proving the Lipschitz estimate
mentioned last time, and then couldn't prove the triangle inequality
efficiently. (Hint: someone should have suggested the Cauchy-Schwarz
inequality.)
Mr. Pal mentioned the following proof
for C: Re(z[conjugate
w])<=|z[conjugate]w|=|z| |[conjugate]w|=|z| |w|.
Finally we began the first lecture of the course. I gave Kronecker's
famous quote:
God created the integers, all else is the work of man.
So we went from the positive integers to the integers to the
rationals. Then briefly I remarked there were many choices of absolute
values on the rationals, and that the "standard" one was rather
exceptional. The rationals can be completed in any of these. We will
choose the real numbers and neglect the p-adics. The real numbers are
ordered, giving rise to other ways of understanding completeness
(logicians are interested in wonderfully huge ordered fields!). So now
we have the complete ordered field, R. Some of its finite
dimensional vector spaces have interesting algebraic structure.
R2 is a field, C, which can't be given a
consistent structure of an ordered field (easy to prove). C
also turns out to be the algebraic closure of R.
R4 is the quaternions (now we give up commutativity:
this is a skew field, and has some neat subgroups).
R8 is the octonions or Cayley numbers (now we give
up associativity as well as commutativity, but this is a division
algebra). I think there is also something interesting still about
R16 but here's a reference with a more complete
discussion:
Numbers by Heinz-Dieter Ebbinghaus (Author), Hans Hermes
(Author), Friedrich Hirzebruch (Author), Max Koecher (Author), Klaus
Mainzer (Author), J�N|rgen Neukirch (Author), Alexander Prestel
(Author), Reinhold Remmert (Author), John H. Ewing (Editor),
K. Lamotke (Introduction), H.L.S. Orde (Translator)
in the library at QA241.Z3413 1990.
I'll discuss the very important material in section 1.5 next time.
| Tuesday,
September 4 | (Lecture #1) |
|---|
I decided to have students begin the class by doing some textbook
homework problems from chapter 1. Let me discuss which problems were
selected and why. (I must admit that I also did this because I thought
it might be fun.)
#9
This problem defined a specific function: i({1-z}/{1+z}), an example of a
linear fractional transformation. It declared that the mapping
established a bijective correspondance between the interior of the
unit circle ("the unit disc") and those complex numbers with positive
real part ("the upper halfplane"). The problem was solved by direct
computation.
Why do this problem?
The problem introduced people to a sort of non-Euclidean view of
geometry. We considered stereographic projection, establishing
a correspondance between points in the plane and all points of the
unit sphere in R3 except the North Pole. It turned out to
be convenient to label this exceptional point  , because then
the correspondance provided a concrete representation of the 1-point
compactification of the plane. It is also one-dimensional complex
projective space, as we shall discuss. Under stereographic projection,
the unit disc corresponds to the lower hemisphere, and the upper
halfplane corresponds to the rear (?) hemisphere. The specific
transformation just turns out to be a description of a rotation of the
unit sphere turning one hemisphere into another. Each of the domains
(unit disc, upper halfplane) is a natural place to explore hyperbolic
geometry. The upper halfplane setting allows a natural group of
transitive automorphisms to operate obviously (translations by real
numbers and multiplications by positive real numbers). The unit disc
model allows the stabilizer of a point, say the origin, to be
described simply: just the rotations. We will need to verify these
things in detail, of course. All the mappings involved are
conformal: they preserve angles defined when C1
paths intersect in the domain and are transformed to the range.
, because then
the correspondance provided a concrete representation of the 1-point
compactification of the plane. It is also one-dimensional complex
projective space, as we shall discuss. Under stereographic projection,
the unit disc corresponds to the lower hemisphere, and the upper
halfplane corresponds to the rear (?) hemisphere. The specific
transformation just turns out to be a description of a rotation of the
unit sphere turning one hemisphere into another. Each of the domains
(unit disc, upper halfplane) is a natural place to explore hyperbolic
geometry. The upper halfplane setting allows a natural group of
transitive automorphisms to operate obviously (translations by real
numbers and multiplications by positive real numbers). The unit disc
model allows the stabilizer of a point, say the origin, to be
described simply: just the rotations. We will need to verify these
things in detail, of course. All the mappings involved are
conformal: they preserve angles defined when C1
paths intersect in the domain and are transformed to the range.
#31
This problem considered "pure" first-order partial differential
operators in x and y. There is a unique pair, {partial/z} and
{partial/z-bar}, which operate well on the functions z and z-bar in C.
Why do this problem?
The text defines holomorphic function to be a C1
function which is annihilated by {partial/z-bar}. Consideration of
this strange definition (one of many logically equivalent statements)
led immediately to the Cauchy-Riemann equations. But why should these
equations be important? We verified that if
f(z)=f(x+iy)=u(x,y)+iv(x,y) has C1 components and if f(z)
is complex differentiable, then the Cauchy-Riemann equations are
satisfied. We began to investigate some sort of converse statement
were true. Some versions are, and we began to prove them. With
C1 assumptions, proof of one statement is almost easy,
using the Mean Value Theorem of one variable calculus. We didn't
exactly finish the proof. Discussion will continue.
We also showed that the L1 and L2 norms are
equivalent in R2. That is, suppose (a,b)=a+ib is in the
plane. Making |a|+|b| small will force
sqrt(a2+b2) small, and conversely. This is true
for any pair of norms in R2 (or, indeed, in
Rn for n finite): not a totally obvious fact. We won't need
the general fact, and will only verify if for pairs of norms we will
encounter. Probably the only other example will be the
L norm, which is max(|a|,|b|).
norm, which is max(|a|,|b|).
Here are other problems I requested, and why I thought they might be
interesting:
#36
Write {partial/z} and {partial/z-bar} in polar coordinates.
Why do this problem?
This is not a very pretty computation, but sometimes we need to do
dirty computations. The result might be useful, so let's see it.
#20 and #24
The first problem is a verification and use of Euler's formula. The
second problem declares that the sum of the kth (k>1)
roots of a complex number must be 0.
Why do this problem?
Both of these problems need the introduction of some notion of the
complex exponential function. So we can explore how the text
introduces this function. We then could get Euler's formula, which has
many uses. The second problem needs Euler's formula to establish the
existence of kth roots!
#23
Prove that |z| is continuous. The text suggests verifying that if
zj->z, then |zj|->|z|.
Why do this problem?
Various irritating approaches can be made to this problem, but maybe
the most satisfying method is to prove
||z|-|w||<=|z-w|
since this declares that |z| is a Lipschitz function and the limit
statements are then clear. C1 functions are locally
Lipschitz, but |z| is certainly not C1 in any neighborhood
of 0.
Verification of the inequality needs work with the Triangle
Inequality, so we would need to think about the Triangle Inequality.
Distances from sets (here |z| measures the distance from 0) typically
arise in a number of analytic problems, and the smoothness (or lack of
smoothness!) is good to be acquainted with.
Maintained by
greenfie@math.rutgers.edu and last modified 9/5/2007.
 To the right is a picture of a male domestic turkey. It has wattles
("a loose fleshy appendage on the head or throat of a turkey or other
birds.") which are sort of enlarged jowls ("the external loose skin on
the throat or neck when prominent."). Certainly the instructor does not look
like a turkey. Domestic turkeys are supposed to be extremely
stupid. Wild turkeys, which are much thinner and mostly brown, are
quite shy and difficult to observe. They do exist on Busch Campus! Try
to find one. (Don't get caught in the Rhus toxicodendron while
seeking the Meleagris gallopavo, please.)
To the right is a picture of a male domestic turkey. It has wattles
("a loose fleshy appendage on the head or throat of a turkey or other
birds.") which are sort of enlarged jowls ("the external loose skin on
the throat or neck when prominent."). Certainly the instructor does not look
like a turkey. Domestic turkeys are supposed to be extremely
stupid. Wild turkeys, which are much thinner and mostly brown, are
quite shy and difficult to observe. They do exist on Busch Campus! Try
to find one. (Don't get caught in the Rhus toxicodendron while
seeking the Meleagris gallopavo, please.)


 This example is maybe a bit more irritating. Define gn by
the following piecewise recipe (really the picture to the right is
what I'm thinking of and I only hope that what follows is
almost correct):
This example is maybe a bit more irritating. Define gn by
the following piecewise recipe (really the picture to the right is
what I'm thinking of and I only hope that what follows is
almost correct):
 Question Can such a function be a folding of the complex plane?
Question Can such a function be a folding of the complex plane?
 A Calc 3 exam problem Let S=[0,2pi]x[0,2pi], a subset of
R2. What's the maximum value of
f(x,y)=sqrt[(sinx)2(cosh)2+(cosx)2(sinhy)2]
on S?
A Calc 3 exam problem Let S=[0,2pi]x[0,2pi], a subset of
R2. What's the maximum value of
f(x,y)=sqrt[(sinx)2(cosh)2+(cosx)2(sinhy)2]
on S?



 Smooth curves through a point z in the domain with some positive angle
are transformed into smooth curves with the same angle through the
corresponding image point, k(z). The curves are rotated by
arg(k´(z)). The local speed along the curves is multiplied
by |k´(z)|. There's just this one rotation and one magnification
factor, so locally the picture is easy (!?) to understand.
Smooth curves through a point z in the domain with some positive angle
are transformed into smooth curves with the same angle through the
corresponding image point, k(z). The curves are rotated by
arg(k´(z)). The local speed along the curves is multiplied
by |k´(z)|. There's just this one rotation and one magnification
factor, so locally the picture is easy (!?) to understand.



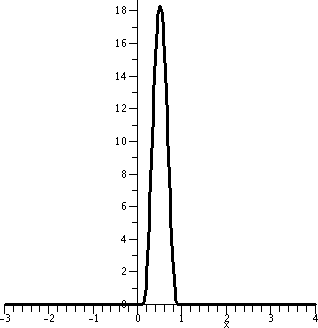
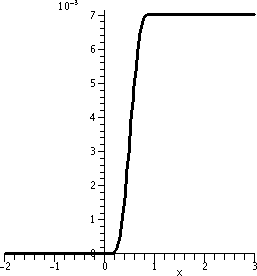

 Maybe a true smooth "bump"
Maybe a true smooth "bump" To do this, we split up the homotopy diagram into tiny rectangles,
around which we knew the integrals were 0. The sides of the
rectangles in the interior canceled each other out, leaving the
integrals along the sides of the homotopy diagrams. The line integrals
at the top and bottom of the diagram are the two we
claimed to be equal. But Mr. Kim wondered, what about the integrals
on the sides of the diagram? Where did they go?
To do this, we split up the homotopy diagram into tiny rectangles,
around which we knew the integrals were 0. The sides of the
rectangles in the interior canceled each other out, leaving the
integrals along the sides of the homotopy diagrams. The line integrals
at the top and bottom of the diagram are the two we
claimed to be equal. But Mr. Kim wondered, what about the integrals
on the sides of the diagram? Where did they go?
 Example
Example Let's give the acute reasoning of Ms. Naqvi here. So let's go from 2 to
800. One way of doing this is to get a path, s, from 2 to 800 in U,
and then "log"(800)=log(2)+
Let's give the acute reasoning of Ms. Naqvi here. So let's go from 2 to
800. One way of doing this is to get a path, s, from 2 to 800 in U,
and then "log"(800)=log(2)+ Now, if we select another disc
DRj(Zj) instead the original
Drj(zj) disc, ie, we have
s([tj-1,tj]) contained in
Drj(zj) and a antiderivative
Fj, and s([tj-1,tj]) contained in
DRj(Zj) and a antiderivative
Gj. In this situation, since both discs are open, the
intersection is a non empty, open, convex set (hence connected),
therefore we can proceed by selecting a unique antiderivative in the 2
discs (this was a HW problem). The Gj and Fj
differ by a constant, as in the previous paragraph.
Now, if we select another disc
DRj(Zj) instead the original
Drj(zj) disc, ie, we have
s([tj-1,tj]) contained in
Drj(zj) and a antiderivative
Fj, and s([tj-1,tj]) contained in
DRj(Zj) and a antiderivative
Gj. In this situation, since both discs are open, the
intersection is a non empty, open, convex set (hence connected),
therefore we can proceed by selecting a unique antiderivative in the 2
discs (this was a HW problem). The Gj and Fj
differ by a constant, as in the previous paragraph.
 So if we add t* with
tj-<t*tj, and we select discs such
that s([tj-1,t*]) is contained in
Da(za), s([t*,tj]) is
contained in Db(zb), with antiderivatives
Fa and Fb respectively, we can prove, using the
same intersection, open, convex, connected argument used above,
that
So if we add t* with
tj-<t*tj, and we select discs such
that s([tj-1,t*]) is contained in
Da(za), s([t*,tj]) is
contained in Db(zb), with antiderivatives
Fa and Fb respectively, we can prove, using the
same intersection, open, convex, connected argument used above,
that The picture to the right is supposed to show the
situation. Sigh. It is complicated. The circle shown in U, to the
right, is the boundary of a disc enclosing the image of one of the
"tiny" rectangles. Good luck in understanding the picture!
The picture to the right is supposed to show the
situation. Sigh. It is complicated. The circle shown in U, to the
right, is the boundary of a disc enclosing the image of one of the
"tiny" rectangles. Good luck in understanding the picture!


 Proof Fix z, and define g(w)=f(w)/(w-z). Then g is holomorphic
in U\{z}. Next we note that C is homotopic in U-{z} to D, the boundary
of a circle of radius v centered at p (v sufficiently small -- such a
disc exists since U is open), hence by Cauchy's Theorem the integral
of g over C is equal to the integral of g over D. A
possible picture of the homotopy is to the right.
Proof Fix z, and define g(w)=f(w)/(w-z). Then g is holomorphic
in U\{z}. Next we note that C is homotopic in U-{z} to D, the boundary
of a circle of radius v centered at p (v sufficiently small -- such a
disc exists since U is open), hence by Cauchy's Theorem the integral
of g over C is equal to the integral of g over D. A
possible picture of the homotopy is to the right.