|
Thursday, November 10 |
|
We had more fun with Fourier series. I reviewed the formulas for Fourier
coefficients. I wrote also how these were used to assemble the Fourier
series for a function. I noted that if a function f were periodic with
period 2Pi, then any interval of length 2Pi will be good for computing
the Fourier coefficients. So, for example, if I wanted a14,
what I wrote last time is (1/Pi)
02Pif(x)cos(14x) dx and the
textbook has (1/Pi)-PiPif(x)cos(14x) dx. But if for
some peculiar reason you wanted to use (1/Pi)668668+2Pif(x)cos(14x) dx you would
get the same answer. Of course, for this, you should realize that the
function f(x) must be periodic with period equal to 2Pi.
Now what should we expect about the Fourier series of f(x)? I really tried to think about the levels of information engineering students should know about Fourier series.
Primary level
(What you really need to know)
On average, if you look at a "high" partial sum of the Fourier series
for f, then random samples of the values of this partial sum will be
close to the values of f(x). A precise statement is that the mean
square error will --> 0 as more terms are taken of the partial
sums.
Secondary level
(What you should know for Math 421)
The sum of whole Fourier series for a function, f, will be f(x) if f
is continuous at x. If f has a jump discontinuity at x, then the sum
of the whole Fourier series will be
(f(x-)+f(x+))/2, the average of the left and
right hand limits of f. Notice, though, that from the point of view of
Fourier series, 0 and 2Pi are the same, so the left side of 0 is the
left side of 2Pi, and the right side of 0 is the right side of
2Pi. Or, if you are considering the interval [-Pi,Pi]. the whole
Fourier series and the partial sums think that -Pi and Pi are the
same.
Comment This property really isn't just for 421, but may also
be useful in applications: I may be exaggerating about my
classifications!
Tertiary level
(What Fourier series enthusiasts might know)
The Gibbs phenomenon: if f has a jump discontinuity at x, then the
partial sums exhibit over and undershoots very near the jump (about 9%
of the jump in directions opposite the jump), and the bumps are
opposite direction of the jump.
Notice, please that the sum of the whole Fourier series does
not does not have this behavior. Its behavior was described
above. I remarked that I did know of some real-world applications
where this Gibbs phenomenon was important, but I didn't know very
many.
I went through the graphical behavior implicit in some of the homework problems. The alert student should be able to see the phenomena described above in these pictures. Actually computing the Fourier series in each case because (if this is being done "by hand") in each case the Fourier coefficients need two integrations by parts.
| F(x)=ex on [-Pi,Pi] | ||
|---|---|---|
| The function itself | The partial sum, up to n=10, of the Fourier series |
The sum of the whole Fourier series |
 |
 |
 |
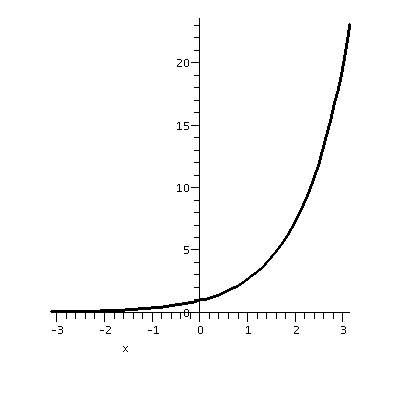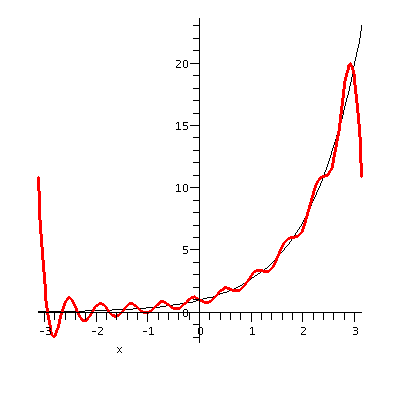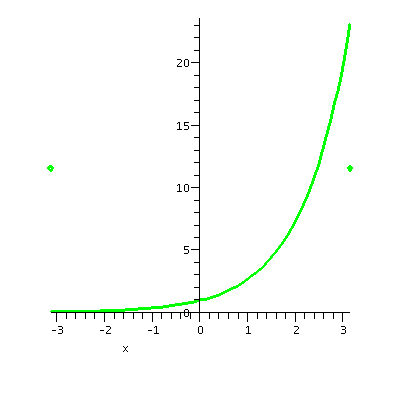| F(x)=x2 on [0,Pi] and 0 on [-Pi,0] | ||
| The function itself | The partial sum, up to n=10, of the Fourier series |
The sum of the whole Fourier series |
 |
 |
 |
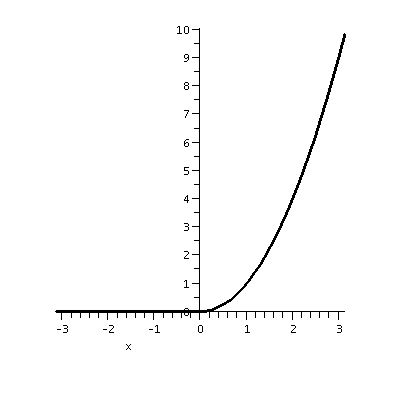Example 1
Suppose f(x)=5sin(x)-2cos(3x)+8cos(17x). What is the Fourier series
of f(x)? This is a very cute problem. The Fourier series of f(x) is
...5sin(x)-2cos(3x)+8cos(17x). It is its own Fourier series. Why is
that? Any other sine/cosine coefficient would be gotten by integrating
(the an or bn formulas). But the
other sine/cosine functions are all orthogonal to these. So, for
example, a17 is gotten by multiplying f(x) by cos(17x) and
integrating from -Pi to Pi. Hey: by orthogonality this is 0. What about
a17? Well, by orthogonality you only need to "worry" about
(1/Pi)-PiPi8(cos(17x))2dx, and (we
discussed this at great length!) this is just 8. The darn 1/Pi in the
original formula is included (orthonormalization!) to make the
coefficient come out correctly.
Example 2
This example is more computationally intricate, especially when done
"by hand". F(x) is defined initially on the interval [0,Pi]. It is
piecewise linear, and is the sort of function we encountered in our
study of Laplace transform methods. The points (0,0) and (Pi/2,1) and
(Pi,1) are on the graph, which suggests that F(x) be (2/Pi)x in the
interval 0<x<Pi/2 and F(x)=1 for Pi/2<x<Pi. I "extended" F(x)
to be 0 in [-Pi,0]. A Maple expression defining such an F(x)
is:
F:=x->piecewise(x>Pi/2,1,x>0,(2/Pi)*x,x>0,0)
I actually computed, by hand, some of the
Fourier coefficients. This involved integrating by parts. I
hope that students can integrate by parts.
I just asked my friend (?) Maple to do the same computation. The results were:
The cosine coefficients, a(n):
Pi n
sin(Pi n) Pi n + 2 cos(----) - 2
2
--------------------------------
2
Pi n
The sine coefficients, b(n):
Pi n
-cos(Pi n) Pi n + 2 sin(----)
2
-----------------------------
2
Pi n
a(0);
3
---
8
The n2's occur because of the integration by parts. I need
to evaluate a(0) separately, since I can't just plug in n=0 in a
formula with n in the bottom (yes, I could use L'Hopital's rule, but I
could also just evaluate the integral).
and just for the fun (?) of it, here is the partial sum up to third
order, of the Fourier series of F(x):
2 cos(x) (Pi + 2) sin(x) cos(2 x) sin(2 x)
3/8 - -------- + --------------- - -------- - 1/2 --------
2 2 2 Pi
Pi Pi Pi
cos(3 x) (3 Pi - 2) sin(3 x)
- 2/9 -------- + 1/9 -------------------
2 2
Pi Pi
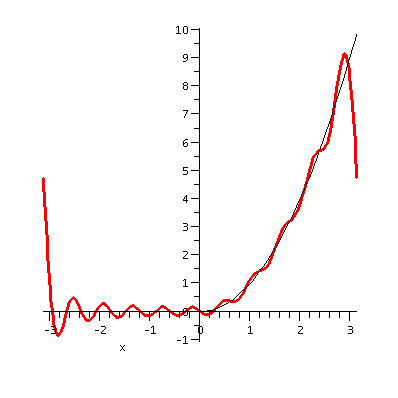
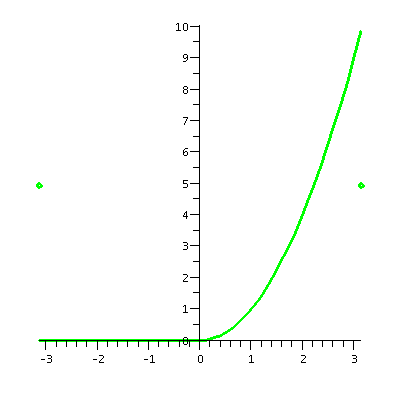
And here is a picture of F(x), a picture of F(x) together with the
10th partial sum of its Fourier series, and a picture of
the sum of the whole Fourier series of F(x). You can see that the
Fourier series is trying to get close to F(x). On most of the
horizontal line segments and on the tilted line, the partial sum of
the Fourier series is wiggling above and below. At the endpoints,
though, the partial sum wants to have the same value at -Pi and Pi. So
the value the partial sum takes is 1/2, the appropriate average of 0
and 1. Also, the Gibbs phenomenon is again visible, if you care about
it.
| F(x)=0 on [-Pi,0], (2/Pi)x on [0,Pi/2], and 1 on [Pi/2,Pi] | ||
|---|---|---|
| The function itself | The partial sum, up to n=10, of the Fourier series |
The sum of the whole Fourier series |
 |
 |
 |
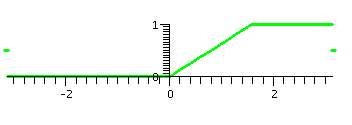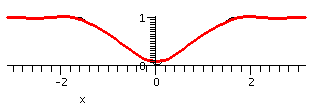
The even extension
There are several standard ways of extending a function defined on
[0,Pi]. One is the even extension, which asks for a function so
that G(-x)=G(x). To get the graph, just flip what you are given across
the y-axis. There are some interesting consequences. One is that all
of the Fourier sine coefficients are 0. Why? Look at
bn=(1/Pi)-PiPiG(x)sin(nx)dx
When we change x to -x, the integrand, G(x)sin(nx) changes to
F(-x)sin(-nx) which is the same as -F(x)sin(nx). Since we're looking
at an interval balanced around 0 (from -Pi to Pi) the contribution at
x of G(x)sin(nx) is exactly balanced out by -G(x)sin(nx) at -x. So all
of the bn's are 0.
I had Maple compute the third partial sum of the Fourier series for the even extension of f. Here it is:
4 cos(x) 2 cos(2 x) cos(3 x)
3/4 - -------- - ---------- - 4/9 --------
Pi Pi Pi
You can see why this is called
the Fourier cosine series for Fon [0,Pi] although it is really
the restriction to [0,Pi] of the Fourier series of the even extension,
G, of F.
I also had Maple graph the even extension and some partial sums. The approximation is really good. Here the sum of the whole Fourier series will exactly be equal to the function -- there are no jumps.
| F(x)=0 on [-Pi,0], (2/Pi)x on [0,Pi/2], and 1 on [Pi/2,Pi] | ||
|---|---|---|
| The function itself | The partial sum, up to n=5, of the Fourier series |
The sum of the whole Fourier series |
 |
 |
 |
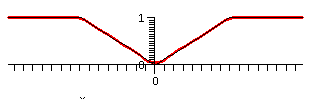The reason I only showed the partial sum up to n=5 above is that the
partial sum up to n=10 is amazingly close to the original
function. Here it is, to the right. I can't see much of a wiggle, and
I can't see much of the original curve at all. It is difficult for me
to believe that this is the sum of 10 cosine functions! The sum of the
whole Fourier cosine series of F (that is, the Fourier series
of the even extension of F) is equal to the original function at all
points of [-Pi,Pi].
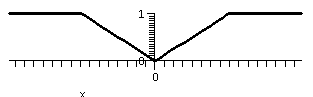
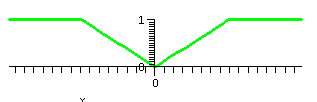
The odd extension
Now with F defined on [0,Pi] we can extend to a function H(x) defined
on [-Pi,Pi] so that
H(x)=F(x) on [0,Pi] and
H(-x)=-H(x). Flip the graph
over the y-axis, and then over the x-axis. Now because
an=(1/Pi)-PiPiH(x)cos(nx)dx
and
H(-x)cos(-nx)=-H(x)cos(nx) using the oddness of this extension, we see
that all of the an's are 0. Here's the beginning of this
Fourier series:
2 (Pi + 2) sin(x) sin(2 x) (3 Pi - 2) sin(3 x)
----------------- - -------- + 2/9 -------------------
2 Pi 2
Pi Pi
Not surprisingly this is called
the Fourier sine series for F on [0,Pi] although it is really
the restriction to [0,Pi] of the Fourier series of the odd extension,
H, of F.
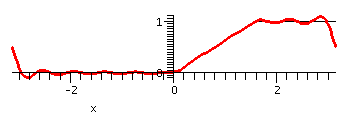
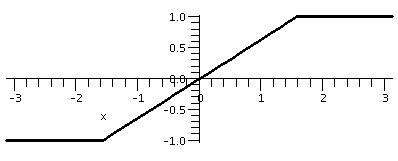
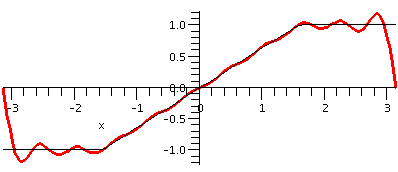
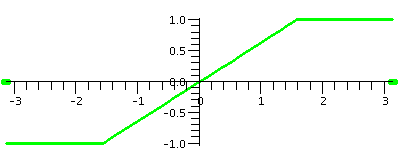
Here are some Maple graphs of the odd extension of together with the sum of the first 10 terms of the Fourier sine series (up to and including the sin(10x) term). The series gets quite close on the tilted line segment, and attempts to be near the two horizontal segments. Of course, there is, in effect, a jump discontinuity at -Pi and Pi. From the Fourier point of view, the odd extension is repeated every 2Pi. So at, for example, x=Pi, the function has a left limit of 1 and a right limit of -1, so the series hops from 1 to -1. To me the Gibbs bumps are showing up.
| F(x)=-1 on [-Pi,-Pi/2], (2/Pi)x on [-Pi/2,Pi/2], and 1 on [Pi/2,Pi] | ||
|---|---|---|
| The function itself | The partial sum, up to n=5, of the Fourier series |
The sum of the whole Fourier series |
 |
 |
 |
The sum of the Fourier sine series of F (that is, the Fourier series of the odd extension of F) is equal to the original function except at the ends Pi and -Pi, where it averages the left and right behavior.
HOMEWORK
I strongly suggest that some time be spent in the next few days
reviewing for the exam. I suggest doing some problems in
12.1-12.3. Also, you should read the review
material.
|
Monday, November 7 |
|
abf(x)g(x) dx=0.
Example
Here is an example suitable for a math course: suppose
f(x)=ex and g(x)=x+C. Can you find C so that f(x) and g(x)
are mean-square orthogonal on [0,1]?
Well, this means we want
01ex(x+C) dx=0.
Now ex(x+C)=xex+Cex has antiderivative
xex-ex+Cex, so the definite integral
(sigh, that stuff with ]x=0x=1) gives
Ce-(-1+C). For this to be 0, we require C(e-1)+1=0 or C=-1/(e-1).
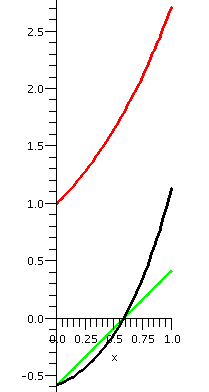
To the right are some pictures: the red curve is ex for x in the unit interval. The light green curve is x+C with C=-1/(e-1). Of course, the black curve is the product ex(x+C). It is supposed to be true that the area above the x-axis for the black curve is equal to the area below the x-axis for the black curve. That's what orthogonality means here.
Trig functions
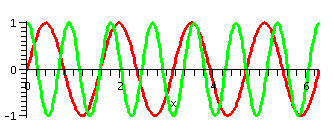The preceding example has little significance, as far as I know. But
now we will verify something more interesting: the two functions
sin(4x) and cos(7x) are orthogonal on [0,2Pi]. The first graph shown
to the right has the graph of these two functions displayed on the
interval mentioned. To me, the orthogonality of these two functions is
not obvious.
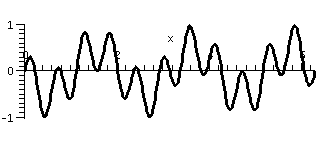The graph shows the prodcut, sin(4x)cos(7x), on the interval
[0,2Pi]. Is it now obvious that the integral is equal to 0?
Well, maybe ... but I think I would have to concentrate a
bit. Instead, we'll verify the orthogonality algebraically. Recall
from the first lecture:
| eit=cos(t)+i sin(t) and cos(t)=[eit+e-it]/2 and sin(t)=[eit-e-it]/(2i) |
|---|
Which leads to ...
Change t to -t in the formula, add, and divide by 2. The result is
cos(t)=(1/2)(ei(t)+e-i(t)).
If we substract them and divide by 2i the result is
sin(t)=(1/[2i])(ei(t)-e-i(t)).
How to antidifferentiate sin(4x)cos(7x)
Change t to 4x and write
sin(4x)=(1/[2i])(ei(4x)-e-i(4x)). Change t
to 7x and write
cos(7x)=(1/2)(ei(7x)+e-i(7x)).
Then
sin(4x)cos(7x)=
(1/2)(1/[2i])(ei(4x)-e-i(4x))(ei(7x)+e-i(7x))=
(1/2)(1/[2i])(ei(11x)-ei(3x)+ei(-3x)-ei(-11x)).
Now suppose that (INTEGER) is
a non-zero integer, positive or negative.
Then 02Piei(INTEGER)x dx=1/(i(INTEGER))ei(INTEGER)x]02Pi.
But when x=0 this is 1. And when x=2Pi(INTEGER)i, it is also 1 since
sin((INTEGER))=0 and cos((INTEGER))=1.
Wow! So each of the four pieces of the sin(4x)cos(7x) integral
evaluates to 0.
Something similar could be done for sin(4x) and sin(7x), and for cos(4x) and cos(7x). Many pairs of these functions are orthogonal.
Family of orthogonal functions
In fact, we have a family of orthogonal functions:
{sin(nx),cos(mx)} where n is a positive integer and m is a
non-negative integer. Every distinct pair of these functions is
orthogonal. By :distinct" I mean that a function won't be orthogonal
to itself. For example, sin(3x) multiplied by sin(3x) on [0,2Pi]
doesn't have its integral equal to 0!
Note that we don't need negative n's and m's since sin(-3x)=-sin(3x),
so 02Pisin(-3x)sin(3x) dx isn't 0. Similarly for cos(-3x)=cos(3x).
In the family {sin(nx),cos(mx)} we don't really need the
function sin(0x) since that is 0. We do, however, need the
function cos(0x): that's 1.
Minimize the mean square energy
I remarked that the mean square norm, the integral of a function
squared on an interval, was frequently identified as energy. So here
is my task: given some function f(x) on [0,2Pi], consider the
following function of, say, 7 variables:
E(a0,a1,a2,a3,b1,b2,b3)=02Pi(f(x)-(a0+a1cos(x)+a2cos(2x)+a3cos(3x)+b1sin(x)+b2sin(2x)+b3sin(3x)))2dx
This is a complicated function of seven (!)
variables. Notice, please, that "x" is not a variable in
E: it is internal to the integral. How can we minimize
this function? This amounts to getting the best mean square
approximation to f(x) by a trigonometric polynomial of the type
given.
One reason to use squares is that they are differentiable. And the function E is certainly differentiable, although maybe it looks very complicated. Why should we expect or even hope that E has a minimum value? Well, since it is the integral of a square, E's value is at least 0. So certainly E is bounded below. It therefore can't run off to -infinity as the values of the parameters change.
The function E must have its minimum at a critical point,
where all of its first derivatives are 0. Let's look at the first
derivative of E with respect to b2:
dE/db2=
d/db202Pi(STUFF)2dx=02Pi2STUFF(dSTUFF/db2) dx.
Since STUFF is
f(x)-(a0+a1cos(x)+a2cos(2x)+a3cos(3x)+b1sin(x)+b2sin(2x)+b3sin(3x))
I know that
d/db2 of it is just sin(2x). So we need to compute
202Pi(f(x)-(a0+a1cos(x)+a2cos(2x)+a3cos(3x)+b1sin(x)+b2sin(2x)+b3sin(3x)))sin(2x) dx. But we have shown that sin(2x) is orthogonal to 1 and cos(x) and cos(2x) and cos(3x) and sin(x) and sin(3x). So a bunch of terms (six of them!) "drop out" of this integral (they are all 0!) and we are left with
202Pi(f(x)-(b2sin(2x)))sin(2x) dx. This is
202Pi
f(x)sin(2x)-b2sin(2x)sin(2x) dx.
When is this equal to 0? The 2 drops out, and this occurs when
b2=02Pif(x)sin(2x) dx/02Pi(sin(2x))2dx.
The formulas
The best mean square approximation to f(x) on [0,2Pi] by a sum of trig
polynomials occurs when
am=02Pif(x)cos(mx) dx/02Pi(cos(mx))2dx for m>=0
bn=02Pif(x)sin(nx) dx/02Pi(sin(nx))2dx for n>0.
The constants
We actually saw formulas like this before when we discussed
orthonormal bases, and how to compute the coefficients for a linear
combination in such a basis. The numbers
02Pi(cos(mx))2dx and
02Pi(sin(nx))2dx are normalization constants, and make the lengths of the appropriate vectors equal to 1 (they "normalize" the lengths).
Here I know that the normalization constants must be
Pi. There is one exception. That is when m=0, and we have cos(0x)=1
for all x. Then the constant is 12=1 integrated over
[2,2Pi], so it must be 2Pi.
Explanation Since sin2+cos2=1 and [0,2Pi]
is a multiple of several full periods of sin(nx) and cos(mx), then, since
integral of 1 over [0,2Pi] is 2Pi, and the shapes of sin2 and
cos2 are the same, they each have integral equal to Pi.
The Fourier series of a function
If F(x) is a function defined on the interval [0,2Pi], define
an=(1/Pi)02PiF(x)cos(nx)dx
bn=(1/Pi)02PiF(x)sin(nx)dx
The Fourier series of F(x) is the infinite series of functions
a0/2+SUMN=1infinity(ancos(nx)+bnsin(nx))
where
an=(1/Pi)02PiF(x)cos(nx) dx
for n integer, n>=0
bn=(1/Pi)02PiF(x)sin(nx) dx
for n integer, n>0
Weird things to note
Well, these are weird but they are what's usual in the subject. Notice
that the a0 term is divided by 2. That's because the
normality constant for cos(0x) is 2Pi, not Pi. And also notice
that the rest of the normalizing constants come off the formulas for
the coefficients. In many standard linear algebra contexts, the darn
formulas have the normalizations (those silly square roots) somehow in
both the vectors and the coefficients of the vectors. Maybe what is
done with Fourier series is more sensible.
You tell me how the Fourier series of a function relates to the function
I gave the class a handout. I
wanted, in observation and discussion with students, to
discover relationships (some subtle) between a function and its
Fourier series (or, rather, since one can't add up all of any
real infinite sum, the partial sums of the Fourier series): more
heuristic stuff.
I would also like to have the Maple commands shown there
available for you to copy, if you have the time and desire to
experiment with them. Here they are:
>Q(3);
2
2 Pi
----- + 2/5 cos(x) - 2/5 Pi sin(x) + 1/10 cos(2 x)
15
- 1/5 Pi sin(2 x) + 2/45 cos(3 x) - 2/15 Pi sin(3 x)
Each coefficient is gotten by integrating by parts twice.
| This F(x) and the 3rd partial sum of its Fourier series |
This F(x) and the 10th partial sum of its Fourier series |
This F(x) and the 20th partial sum of its Fourier series |
|---|---|---|
 |
 |
 |
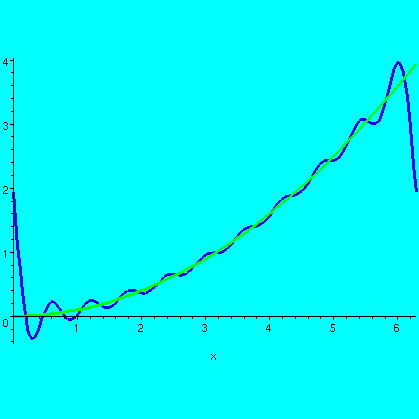
The graphs of the Q(n)'s (the partial sums) get closer to the graph of F(x) as n increases.
What does closer mean? This turns out to be a rather difficult question, both theoretically and in practice.
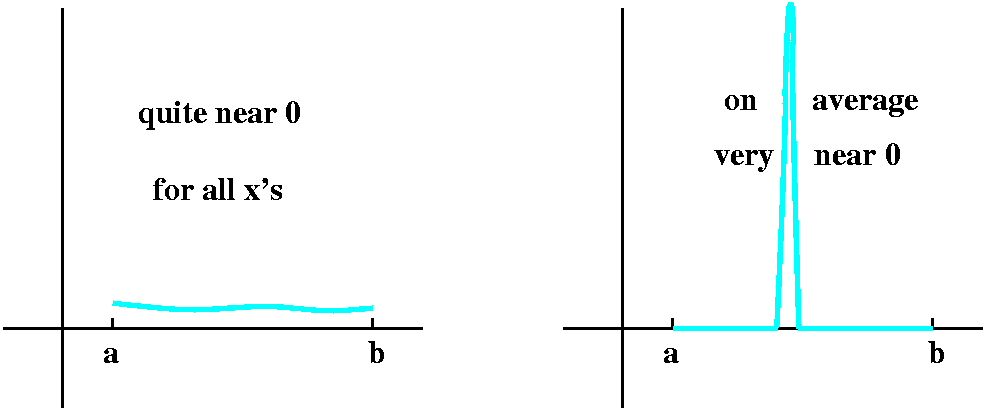
The pictures should show some of the difficulty. For example, you may
want a function to be small on [a.b]. A very strict
interpretation might be to have the values, f(x), very close to 0 for
all x. But suppose you were really modelling some process which you
expected to sample, somehow "randomly", on the interval, a few times
(10 or 100 or ...). Maybe you would be happy enough controlling the
average distance to 0. So things are complicated.
In the pictures of our function F(x) and various partial sums, inside the interval the partial sums are getting close to the values of the function. At the end points (0 and 2Pi) they aren't getting close ... what the heck. Also, if you look really closely at the graphs, you can see tiny bumps near the "ends" which represent some complicated phenomena. Well, one thing at a time.
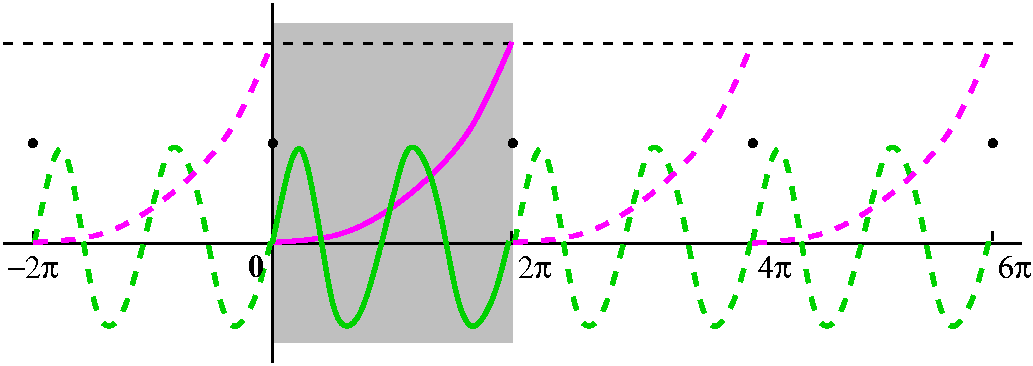
What the Fourier series sees...
We get the Fourier coefficients by integrating the product of a sine
or cosine on [0,2Pi] (the solid green curve) by our function F(x) (the
solid magenta [?]) curve). One point of view is that everything goes
on inside the shaded box. But the trig function goes on forever, and it
is periodic with period 2Pi. To the trig function, our F(x) might as
well be "extended" with period 2Pi to the left and to the right
forever. Notice that the trig function will try at, say, 0, to
approximate the values from both the left and right of the extended
F(x). This extended F(x) has a jump discontinuity at 0, and the trig
function, in trying its approximation, settles on being halfway
between the ends of the jump. This is the collection of black dots in
the picture at half the height of F(x) at x=2Pi.
The partial sums of the Fourier series try very hard to get close to F(x). If F is continuous at x, then they will converge to F(x). If F has a jump discontinuity at x, then they will converge to the average (really!) of the left and right hand limits of F at x (the middle of the jump).
Gibbs: the overshoot
J.
Willard Gibbs received the first U.S. doctorate in engineering in
1863. He saw that at a jump discontinuity, there is always an
overshoot of about 9% in the Fourier series. On the top side, the
overshoot is above, and on the bottom side, below. These bumps get
narrower and closer to the jump, but they never disappear!
A Heaviside example
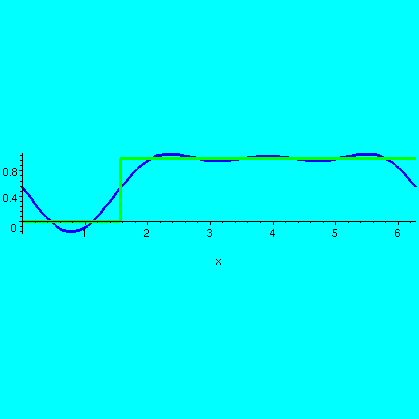
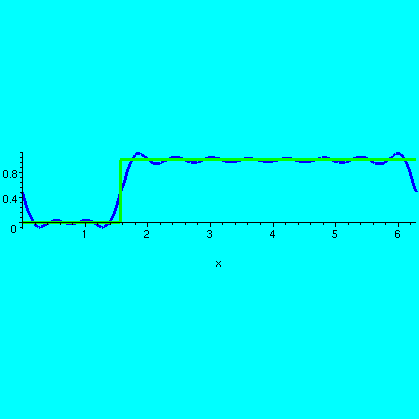
The next example on the handout was U(x-{Pi/2}), the Heaviside
step or jump at Pi/2. This function is 0 to the left of Pi/2 and is 1
to the right of Pi/2. In Maple, the following formula
describes the function: F:=x->piecewise(x<Pi/2,0,1);
Here are the pictures for this function.
| This F(x) and the 3rd partial sum of its Fourier series |
This F(x) and the 10th partial sum of its Fourier series |
This F(x) and the 20th partial sum of its Fourier series |
|---|---|---|
 |
 |
 |
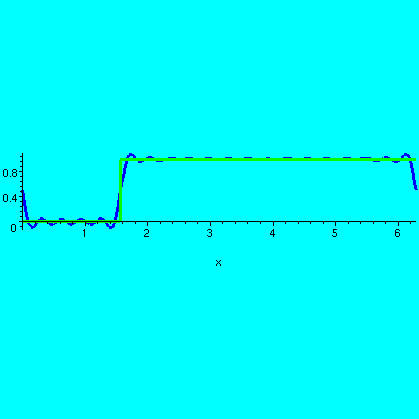I hope you see that the partial sums detect two jump discontinuities, one at Pi/2, certainly, but another one at 0=2Pi (well, they are the same numbers to sine and cosine) as well!
Taylor and Fourier compared
I tried to take a fairly random function defined by a fairly simple
formula: F(x)=sqrt(16+x2+x3). Then I had
Maple create the degree 12 Taylor
polynomial for F(x) at x=0. I also had Maple create
the Fourier series summed up to the n=6 terms in
both sine and cosine: this is what is defined as Q(6) above. I
admit that the computation of Q(6) took more time than the computation
of the Taylor polynomial, but not a great deal
more time. Here are three pictures.
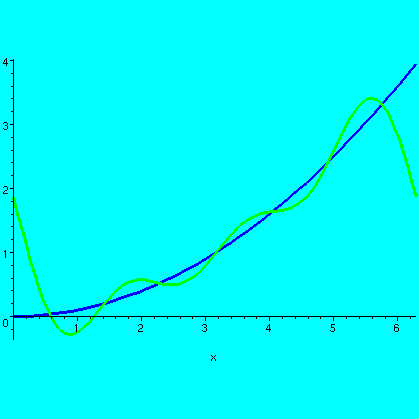
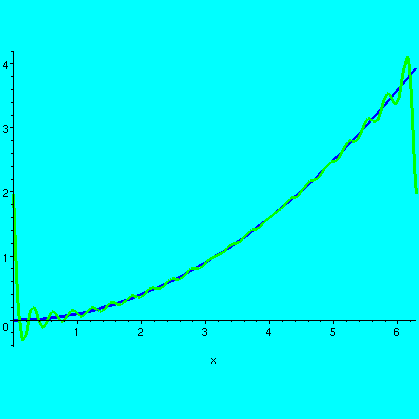
| This is the Taylor polynomial compared with the function in the interval [0,3]. For much of the left-hand portion of this interval, the Taylor polynomial and the function graph overlay one another. |  |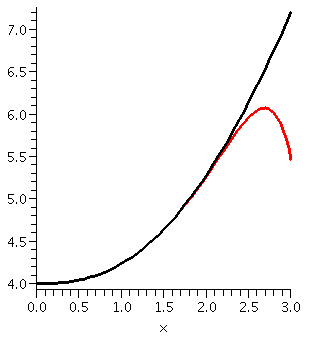
| Now the Taylor polynomial and the function are shown on all of [0,2Pi]. Please note the scale on the vertical axis. There is enormous discrepancy between the function and the polynomial for much of the domain. |  |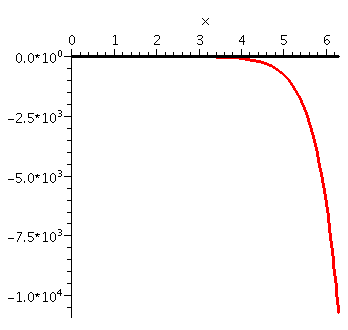
| Here is the Fourier approximation together with the function on all of [0,2Pi]. There is certainly some deviation, but the deviation is controlled and only affects a small part of the domain. On average these functions are rather close. |  |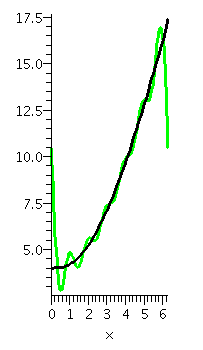
The exam
The exam will cover our work on linear algebra and sections 12.1-12.3 of the textbook, which we will discuss this week.
Textbook problems
We won't have time to give and get back graded homework. But the fine
students listed below associated with the textbook homework problems
indicated (from the syllabus) have agreed to try to write solutions
which I will scan and put on the web.
12.1: 3, Mr. Sequeira
12.1: 7, Ms. Launay
12.1: 17, Mr. Weinstein
12.2: 1, Ms. Tagle
12.2: 5, Ms. Rose
12.2: 9, Mr. Clark
12.2: 15, Mr. Boege
12.2: 17, Mr. Mostiero
Earn 5 points
You can earn 5 points towards your score on the next exam by answering some questions. The rules are
on that page.
HOMEWORK
You should read sections 12.1-12.3 of the text. Today we covered much
of 12.1 and 12.2, and I hope to discuss 12.3 on Thursday. I would
suggest that you try several of the homework problems assigned in 12.1
and 12.2, and even look at the other textbook problems and consider if
you can do them.
Maintained by greenfie@math.rutgers.edu and last modified 9/2/2005.