11. I) Set up the triple integral
int int intR f(x,y,z) dV
where R is the region inside the sphere
x2+y2+z2=2 and
inside the cone z2=x2+y2
(inside the cone means z2>=x2+y2)
in the following systems of coordinates:
a) Rectangular;
b) Cylindrical;
c) Spherical.
II) Evaluate the volume of the region R described in part I.
 a)
We set up the triple integral over the region R where R is inside the sphere
x^2+y^2+z^2=2 and inside the cone z^2=x^2+y^2 in the rectangular system of
coordinates.
a)
We set up the triple integral over the region R where R is inside the sphere
x^2+y^2+z^2=2 and inside the cone z^2=x^2+y^2 in the rectangular system of
coordinates.
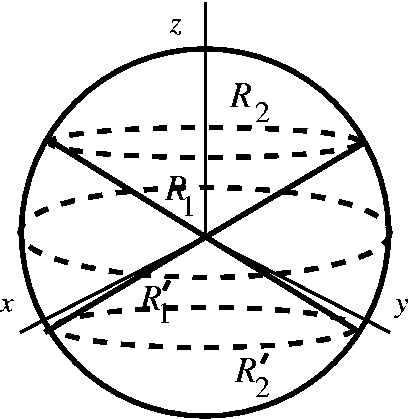
First, we divide the solid into four parts, the cone z=(x^2+y^2)^(1/2) above
z=0 and below z=1(We denote this R1) and the solid above z=1 and below
x^2+y^2+z^2=2 (We denote this R2).
Similarly, the cone z=(x^2+y^2)^(1/2) below z=0 and above z=-1 (We denote
this R1') and the solid below z=-1 and above x^2+y^2+z^2=2 (We denote this
R2').
For R1 and R1';
If we cut the cone along xy-plane first, we get a circle (x^2+y^2)^(1/2)=+-z
on the xy-plane. The boundary of +z is (x^2-y^2)^(1/2)<=z<=1 where the
lower boundary moves as x and y change, and the boundary of -z
is -1<=z<=-(x^2-y^2)^(1/2) where the upper boundary moves as x and y change.
So we compute the iterated integral of the circle (x^2+y^2)^(1/2)=z with
assuming z is constant. The boundary of y, x should be where x^2+y^2=1,
so -(1-x^2)^(1/2)<=y<=(1-x^2)^(1/2), and -1<=x<=1.
Thus we can express R1and R1' as the following;
R1={(x,y,z)|-1<=x<=1, -(1-x^2)^(1/2)<=y<=(1-x^2)^(1/2),(x^2+y^2)^(1/2)<=z<=1
}
R1'={(x,y,z)|-1<=x<=1, -(1-x^2)^(1/2)<=y<=(1-x^2)^(1/2), -1<=z<=-(x^2+y^2)^(
1/2)}
Therefore, we have
int(-1to1){int(-(1-x^2)^(1/2))to(1-x^2)^(1/2))[int((x^2+y^2)^(1/2)to1)f(x,y,
z)dz]dy}dx
and
int(-1to1){int(-(1-x^2)^(1/2))to(1-x^2)^(1/2))[int(-1
to -(x^2+y^2)^(1/2))f(x,y,z)dz]dy}dx.
For R2 and R2':
Similarly if we cut the cone along xy-plane, we get a circle
(x^2+y^2)^(1/2)=+-z on the xy-plane. Then the boundary of +z is
1<=z<=(2-x^2-y^2)^(1/2) where the upper boundary moves as x and y change,
and the boundary of -z is -(2-x^2-y^2)^(1/2)<=z<=-1 where the lower boundary
moves as x and y change.
We compute the iterated integral of the circle (x^2+y^2)^(1/2)=z in the same
way as R1, so we get -(1-x^2)^(1/2)<=y<=(1-x^2)^(1/2), and -1<=x<=1.
We can express R2 as the following;
R2={(x,y,z)|-1<=x<=1, -(1-x^2)^(1/2)<=y<=(1-x^2)^(1/2),1<=z<=(2-x^2-y^2)^(1/
2)}
R2'={(x,y,z)|-1<=x<=1, -(1-x^2)^(1/2)<=y<=(1-x^2)^(1/2), -(2-x^2-y^2)^(1/2)<
=z<=-1}.
Therefore, we have
int(-1to1){int(-(1-x^2)^(1/2))to(1-x^2)^(1/2))[int(1to(2-x^2-y^2)^(1/2))f(x,
y,z)dz]dy}dx
and
int(-1to1){int(-(1-x^2)^(1/2))to(1-x^2)^(1/2))[int(-(2-x^2-y^2)^(1/2)to -1)f
(x,y,z)dz]dy}dx
Therefore, R=R1+R2+R1'+R2', so the triple integral over R is;
int(-1to1){int(-(1-x^2)^(1/2))
to(1-x^2)^(1/2))[int((x^2+y^2)^(1/2)to1)f(x,y,z)dz]dy}dx
+ int(-1to1){int(-(1-x^2)^(1/2))to(1-x^2)^(1/2))[int(1
to(2-x^2-y^2)^(1/2))f(x,y,z)dz]dy}dx
+int(-1to1){int(-(1-x^2)^(1/2))to(1-x^2)^(1/2))[int(-1to -(x^2+y^2)^(1/2))f(
x,y,z)dz]dy}dx
+
int(-1to1){int(-(1-x^2)^(1/2))to(1-x^2)^(1/2))[int(-(2-x^2-y^2)^(1/2)to -1)f
(x,y,z)dz]dy}dx
b)We set up the triple integral over the region R where R is inside the
sphere x^2+y^2+z^2=2 and inside the cone z^2=x^2+y^2 in the cylindrical
system of coordinates.
Let x=r*sin(theta), y=r*cos(theta), z=z.
Similar to a), we divide the solid into four parts, the cone
z=(x^2+y^2)^(1/2) above z=0 and below z=1(We denote this R1), the solid
above z=1 and below x^2+y^2+z^2=2 (We denote this R2), the cone
z=(x^2+y^2)^(1/2) below z=0 and above z=-1 (We denote this R1') and the
solid below z=-1 and above x^2+y^2+z^2=2 (We denote this R2').
For R1 and R1', when we cut the solid parallel to xy-plane, we get the
circle x^2+y^2=r^2=z^2, therefore, the boundary of r is 0<=r<=z, 0<=r<=-z,
respectively.
For R2 and R2', we get the circle x^2+y^2==r^2=2-z^2 where z is fixed.
therefore,the boundary of r is 1<=r<=(2-z^2)^(1/2) for both regions.
Therefore these regions can be expressed by
R1={(r,theta,z)|0<=theta<=2*pi, 0<=r<=z, 0<=z<=1}
R1'={(r,theta,z)|0<=theta<=2*pi, 1<=r<=(2-z^2)^(1/2), 1<=z<=sqrt(2)}
R2={(r,theta,z)|0<=theta<=2*pi, 0<=r<=z, -1<=z<=0}
R2'={(r,theta,z)|0<=theta<=2*pi, 1<=r<=(2-z^2)^(1/2), -sqrt(2)<=z<=-1}
Thus we get
int(0to1){int(0to2*pi)[int(0toz)f(r*cos(theta),r*sin(theta),z)rdr]d(theta)}d
z
+ int(1to sqrt(2)){int(0to2*pi)[int(1to
(2-z^2)^(1/2))f(r*cos(theta),r*sin(theta),z)rdr]d(theta)}dz
+int(-1to0){int(0to2*pi)[int(0toz)f(r*cos(theta),r*sin(theta),z)rdr]d(theta)
}dz
+
int(-sqrt(2)to-1){int(0to2*pi)[int(1to(2-z^2)^(1/2))f(r*cos(theta),r*sin(the
ta),z)rdr]d(theta)}dz
c) We set up the triple integral over the region R where R is inside the
sphere x^2+y^2+z^2=2 and inside the cone z^2=x^2+y^2 in the spherical
system of coordinates.
Let x=rho*sin(phi)*cos(theta), y=rho*sin(phi)*sin(theta), z=rho*cos(phi).
We divide the solid into two parts, the solid above z=0 (R1) and the solid
below z=0 (R2).
Notice that rho^2=x^2+y^2+z^2, so the boundary of rho is 0<=rho<=sqrt(2).
Then we get
R1={(rho,theta,phi)|0<=rho
Thus we get
int((0 to 2*pi){int(0 to pi/4) [int(0 to sqrt(2)) f(rho*sin(phi)*cos(theta),
rho*sin(phi)*sin(theta),rho*cos(phi))(rho)^2 sin(phi) d(rho)]d(phi)}d(theta)
+ int((0 to 2*pi){int(3*4/pi to pi) [int(0 to sqrt(2)
f(rho*sin(phi)*cos(theta), rho*sin(phi)*sin(theta),rho*cos(phi))(rho)^2
sin(phi) d(rho)]d(phi)}d(theta).
II) We choose the system of coordinates of the simplest computation, c) and
evaluate the volume of R.
We take f(rho*sin(phi)*cos(theta), rho*sin(phi)*sin(theta),rho*cos(phi))=1
so that we can get the volume of R.
Also, the volume of R1=the volume of R2, so we compute only R1 and double
it.
Then
int(0 to 2*pi){int(0 to pi/4) [int(0 to sqrt(2) (rho)^2 sin(phi)
d(rho)]d(phi)}d(theta)
=int(0 to 2*pi){int(0 to pi/4) [(1/3) (rho)^3 sin(phi)](0 to
sqrt(2))d(phi)}d(theta)
=int(0 to 2*pi){int(0 to pi/4) [(2*sqrt(2)/3*sin(phi)]d(phi)}d(theta)
=int(0 to 2*pi)[-(2*sqrt(2))/3*sin(phi)](0 to pi/4)d(theta)
=int(0 to 2*pi)[((2*sqrt(2)+2)/3]d(theta)
=[(4*sqrt(2)-4)*pi]/3
Therefore the volume of R is [(8*sqrt(2)-8)*pi]/3.
Comment by the management Yes, this problem was given by
one of my colleagues in a recent Math 291 exam. The problem and the
solution are long. I can't offer any serious "shortening" comments to
the solution given above.
Sent by Atsuko Odoi on Thu, 21 Nov 2002 14:23:14
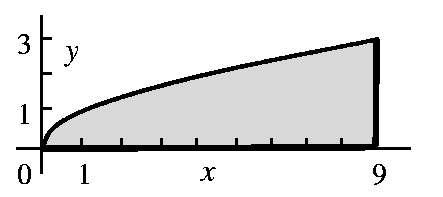 Reversing the order of integration results in the following limits of
integration: x is integrated from 0 to 9 and y goes from 0 to
sqrt(x).
These limits can be found through analysis of a graph of the original
limits.
Reversing the order of integration results in the following limits of
integration: x is integrated from 0 to 9 and y goes from 0 to
sqrt(x).
These limits can be found through analysis of a graph of the original
limits.

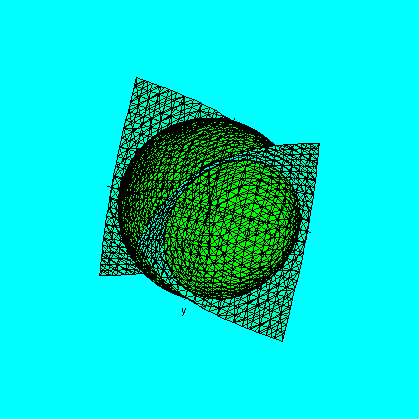
 a)
We set up the triple integral over the region R where R is inside the sphere
x^2+y^2+z^2=2 and inside the cone z^2=x^2+y^2 in the rectangular system of
coordinates.
a)
We set up the triple integral over the region R where R is inside the sphere
x^2+y^2+z^2=2 and inside the cone z^2=x^2+y^2 in the rectangular system of
coordinates.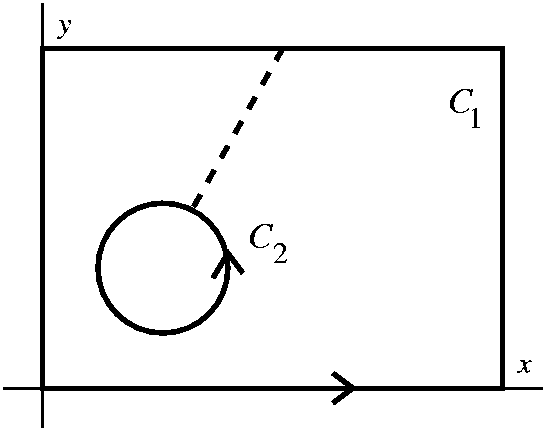 To find this line integral, we can use Green's Theorem on the area
between to two curves, and then add the line integral along C_2 to the
result. In order to use Green's Theorem, first picture a curve that
travels counter-clockwise around C_1, at some point stops and travels
inward to C_2, travels clockwise around C_2, then travels back along the
same line joining the two original curves, and then completes the
original path of C_1. (I know this is incredibly hard to see without an
actual picture, but bear with me.) The resulting enclosed area is the
region between the two original curves. According to Green's Theorem,
since M and N are continuous and differentiable on this region the
line integral of Mdx + Ndy along the strange curve described above
is equal to int int_R N_x - M_y dA.
To find this line integral, we can use Green's Theorem on the area
between to two curves, and then add the line integral along C_2 to the
result. In order to use Green's Theorem, first picture a curve that
travels counter-clockwise around C_1, at some point stops and travels
inward to C_2, travels clockwise around C_2, then travels back along the
same line joining the two original curves, and then completes the
original path of C_1. (I know this is incredibly hard to see without an
actual picture, but bear with me.) The resulting enclosed area is the
region between the two original curves. According to Green's Theorem,
since M and N are continuous and differentiable on this region the
line integral of Mdx + Ndy along the strange curve described above
is equal to int int_R N_x - M_y dA.